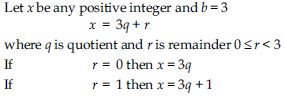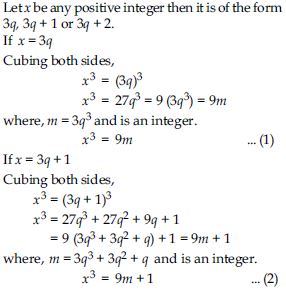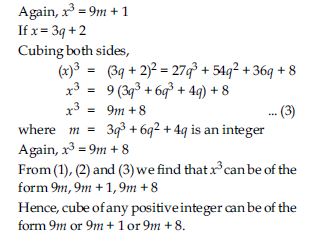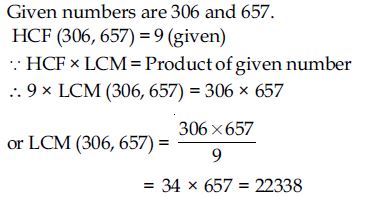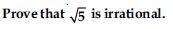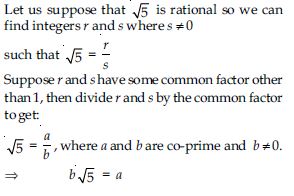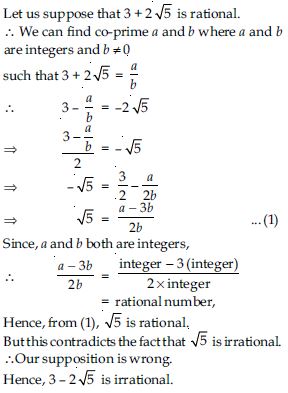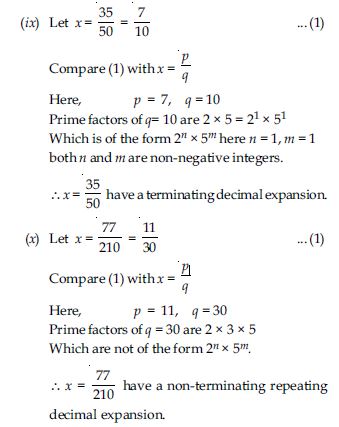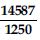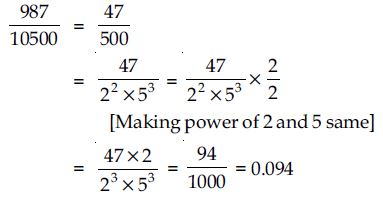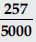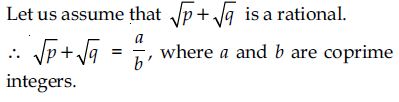NCERT Solutions for Class 10 Math Chapter 1 - Real Numbers

Answer:

1. By division Algorithm

   Step 1: Since 225 > 135, we apply the division lemma to 225 and 135, we get 225 = 135 x 1 + 90

   Step 2: Since the remainder 90 $\ne$ 0, we apply the division lemma to 135 and 90, we get 135 = 90 x 1 + 45

   Step 3: Since the remainder 45 $\ne$ 0, we apply the division lemma to 90 and 45, we get 90 = 45 x 2 + 0

   Since the remainder has now become zero, so we stop the procedure.

   ∵ Divisor in the step 3 is 45.

   ∴ HCF of 90 and 45 is 45.

   Hence, HCF of 135 and 225 is 45.

2. Hence, HCF of 135 and 225 is 45.

   Since, 38220 > 196, we apply the division lemma to 196 and 38220, we get 38220 = 196 x 195 + 0

   Since the remainder has now become zero, so we stop the procedure.

   ∵ Divisor in the step 1 is 196

   ∴ HCF of 38220 and 196 is 196.

   Hence, HCF of 38220 and 196 is 196.

3. To find HCF of 867 and 255

   Step 1: Since 867 > 255, we apply the division lemma to 867 and 255, we get 867 = 255 x 3 + 102

   Step 2: Since remainder 102 $\ne$ 0, we apply the division lemma to 255 and 102, we get 255 = 102 x 2 + 51

   Step 3: Since remainder 51 $\ne$ 0, we apply thedivision lemma to 51 and 102, by taking 102 as dividend, we get 102 = 51 x 2 + 0

   Since the remainder has now become zero, so we stop the procedure.

   ∵ Divisor in step 3 is 51

   ∴ HCF of 102 and 51 is 51.

   ∴ HCF of 102 and 51 is 51.

Answer:

Let a be any positive odd integer, we apply the division algorithm with a and b = 6.

Since 0 $\le$ r $<$ 6, the possible remainders are 0, 1, 2, 3, 4 and 5.

i.e., a can be 6q or 6q + 1, or 6q + 2, or 6q + 3, or 6q + 4, or 6q + 5 where q is quotient.

However, since a is odd

∴ a cannot be equal to 6q, 6q + 2, 6q + 4

∴ a cannot be equal to 6q, 6q + 2, 6q + 4

Therefore, any odd integer is of the form 6q + 1
or 6q + 3 or 6q + 5.

Answer:

Total number of members in army = 616 and 32 (A band of two groups)

Since two groups are to march in same number of columns and we are to find out the maximum number of columns.

∴ Maximum number of columns = HCF of 616 and 32

Step 1: Since 616 > 32, we apply the division lemma to 616 and 32, to get 616 = 32 x 19 + 8

Step 2: Since the remainder 8 ≠ 0, we apply the division lemma to 32 and 8, to get 32 = 8 x 4 + 0
Since the remainder has now become zero, so we stop the procedure.

∵ Divisor in the last step is 8

∴ HCF of 616 and 32 is 8

Hence, maximum number of columns in which they can march is 8.

Answer:

Answer:

Answer:

1. Prime factorisation of 140 = (2)² x (35)

   Prime factorisation of 140 = (2)² x (35)

2. Prime factorisation of 156 = (2)² x (39)

   = (2)² x (3) x (13)

3. Prime factorisation of 3825 = (3)² x (425)

   = (3)² x (5) x (85)

   = (3)² x (5)² x (17)

4. Prime factorisation of 5005 = (5) x (1001)

   = (5) x (7) x (143)

   = (5) x (7) x (11) x (13)

5. = (5) x (7) x (11) x (13)

   = (17) x (19) x (23).

Answer:

1. Given numbers are 26 and 91

   Prime factorisation of 26 and 91 are
   26 = (2) x (13)
   and 91 = (7) x (13)
   HCF (26, 91) = Product of least powers of common factors
   ∴ HCF (26, 91) = 13
   and LCM (26, 91) = Product of highest powers of all the factors
   = (2) x (7) x (13) = 182
   Verification:
   LCM (26, 91) x HCF (26, 91) = (13) x (182)
   = (13) x (2) x (91) = (26) x (91)
   = Product of given numbers

2. Given numbers are 510 and 92

   Prime factorisation of 510 and 92 are
   510 = (2) x (255) = (2) x (3) x (85)
   = (2) x (3) x (5) x (17)
   and 92 = (2) x (46) = (2)² x (23)
   HCF (510, 92) = Product of least powers of common factors = 2
   LCM (510, 92) = Product of highest powers of all the factors
   = (2)² x (3) x (5) x (17) x (23) = 23460
   Verification:
   LCM (510, 92) x HCF (510, 92)
   = (2) x (23460)
   = (2) x (2)² x (3) x (5) x (17) x (23)
   = (2) x (3) x (5) x (17) x (2)² x (23)
   = 510 x 92
   = Product of given numbers

3. Given numbers are 336 and 54

   Prime factorisation of 336 and 54 are
   336 = (2) x (168) = (2) x (2) x (84)
   = (2) x (2) x (2) x (42)
   = (2) x (2) x (2) x (2) x (21)
   = (2)4 x (3) x (7)
   and 54 = (2) x (27) = (2) x (3) x (9)
   = (2) x (3) x (3) x (3) = (2) x (3)³
   HCF (336, 54) = Product of least powers of common factors
   = (2) x (3) = 6
   LCM (336, 54) = Product of highest powers of all the factors
   = (2)⁴ x (3)³ x (7) = 3024
   Verification:
   LCM (336, 54) x HCF (336, 54)
   = 6 x 3024 = (2) x (3) x (2)⁴ x (3)³ x (7)
   = (2)⁴ x (3) x (7) x (2) x (3)³ = 336 x 54
   = Product of given numbers.

Answer:

Answer:

Answer:

Let us suppose that 6ⁿ ends with the digit 0 for some n $\in$ N.

∴ 6ⁿ is divisible by 5.
But, prime factors of 6 are 2 and 3
∴ Prime factors of (6)ⁿ are (2 x 3)ⁿ
$\Rightarrow$ It is clear that in prime factorisation of 6ⁿ there is no place for 5.
∵ By Fundamental Theorem of Arithmetic,
Every composite number can be expressed as a product of primes and this factorisation is unique, apart from the order in which the prime factors occur.
∴ Our supposition is wrong.
Hence, there exists no natural number n for which 6n ends with the digit zero.

Answer:

Consider, 7 x 11 x 13 + 13 = 13 [7 x 11 + 1]
which is not a prime number because it has a factor 13. So, it is a composite number.
Also, 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5
= 5 [7 x 6 x 4 x 3 x 2 x 1 + 1], which is not a prime number because it has a factor 5. So it is a composite number.

Answer:

Time taken by Sonia to drive one round of the field = 18 minutes

Time taken by Ravi to drive one round of same field = 12 minutes

They meet again at the starting point = LCM (18, 12)

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

(c) 2m

Answer:

(d) 2q + 1

Answer:

(c) an odd integer

Answer:

(b) 2

Answer:

(a) 13

Answer:

(b) xy²

Answer:

(c) a³b²

Answer:

(a) always irrational

Answer:

(d) 2520

Answer:

(d) four decimal places

Answer:

No. For instance take 33 cannot be written in the form of 4q + 2 for any value of q as an integer.

Answer:

‘‘The product of two consecutive positive integers is divisible by 2’’ is a true statement because one of them has to be even, and a multiple of an odd and an even integer is always even.
∵ Even integer is always divisible by 2.
∴ The product will also be divisible by 2.

Answer:

As we know that three consecutive integers include an integer which is a multiple of 2 and an integer which is a multiple of 3.
∴ The product of three consecutive integers is divisible by 6. Hence, above statement is true.

Answer:

The square of any positive integer cannot be written in the form 3m + 2, where m is a natural number.
As for an example,
Let the number is 4, its square is 16.
But 16 cannot be written as 3m + 2.
∵ 3m + 2 = 16

Answer:

No. Because for any positive integer of the form 3q + 1, its square will be (3q + 1)² = 9q² + 6q + 1 = 3(3q² + 2q) + 1 = 3m + 1

Answer:

∵ The numbers 525 and 3000 are both divisible only by 3, 5, 15, 25 and 75 only.
∴ HCF (525, 3000) = 75
∵ 75 is the highest amongst the common factors.

Answer:

3 x 5 x 7 + 7 = 7(15 + 1)
= 7 x 16 = 7 x 2 x 8
Which has more than two factors.
∴ It is a composite number.

Answer:

HCF must divide LCM but here 18 does not divide 380.
∴ Any two numbers cannot have 18 as their HCF and 380 as their LCM.

Answer:

Answer:

As 327.7081 is a terminating decimal number, so q must be of the form 2^m5ⁿ, where m, n are natural numbers.

Answer:

Any positive integer can be written as:
2n or 2n + 1 for some integer n.
Now, (2n)² = 4n²
= 4p, where p = n²
and (2n + 1)² = 4n² + 4n + 1
= 4(n² + n) + 1
= 4p + 1, p = n² + n
So, square of any positive integer is either in the form 4p or 4p + 1.
So, square of any positive integer is either in the form 4p or 4p + 1.

Answer:

Any positive integer can be written as 4p, 4p + 1,
4p + 2, 4p + 3 for some integer p.
Now, (4p)³ = 64p³ = 4(16p³) = 4n,
where n = 16p³
(4p + 1)³ = 64p³ + 48p² + 12p + 1
= 4(16p³ +12p² + 3p) + 1 = 4n + 1,
where n = 16p³ + 12p² + 3p
(4p + 2)³ = 64p³ + 96p² + 48p + 8
= 4(16p³ + 24p² + 12p + 2) = 4n,
where n = 16p³ + 24p² + 12p + 2
(4p + 3)³ = 64p³ + 144p² + 108p + 27
= 64p³ + 144p² + 108p + 24 + 3
= 4(16p³ + 36p² + 27p + 6) + 3
= 4n + 3,
where n = 16p³ + 36p² + 27p + 6
So, cube of any positive integer is in the form 4n,
4n + 1 or 4n + 3, for some integer n.

Answer:

Since square of any positive integer is of the form 4p or 4p + 1.
So, square of any positive integer cannot be in the form 5p + 2 or 5p + 3 for any integer p.

Answer:

Any positive integer cannot be of the form 6n + 2 or 6n + 5 for any integer n.

Answer:

Any integer is of the form 2n + 1.
Now, (2n + 1)² = 4n² + 4n + 1
= 4(n² + n) + 1
= 4p + 1, where p = n² + n
So, square of any odd integer is in the form 4p + 1.

Answer:

Any odd integer can be written in form of 2p + 1,
for some integer p.
Let n = 2p + 1
Now, n² - 1 = (2p + 1)² - 1
= 4p² + 4p + 1 - 1
= 4p² + 4p
= 4(p² + p)
Since, p² + p = p(p + 1)
So, if p is odd then p + 1 is even, and if p is even
then p + 1 is odd.
$\Rightarrow$In any case p² + p is divisible by 2.
So, n² - 1 is always divisible by 8.

Answer:

x and y are both odd positive integers.
∴ Let x = 2p + 1
and y = 2q + 1, for some integers p and q.
Now, x² + y² = (2p + 1)² + (2q + 1)²
= 4p² + 4p + 1 + 4q² + 4q + 1
= 4p² + 4q² + 4p + 4q + 2
= 4(p² + q² + p + q) + 2
$\Rightarrow$ x² + y² is an even number but not divisible by 4.

Answer:

Here, 441 $<$ 567 $<$ 693.
Let us first take 441 and 567.
567 = 441 x 1 + 126
441 = 126 x 3 + 63
126 = 63 x 2 + 0
So, HCF of 567 and 441 = 63
Now, take 63 and 693.
693 = 63 x 11 + 0
So, HCF of 441, 567 and 693 = 63.

Answer:

The largest number that divides 1251, 9377 and 15628 leaving remainders 1, 2 and 3 respectively is the HCF of (1251 - 1), (9377 - 2) and (15628 - 3).
So, we have to find HCF of 1250, 9375 and 15625.
9375 = 1250 x 7 + 625
1250 = 625 x 2 + 0
∴ HCF of 9375 and 1250 = 625.
Now HCF of 625 and 15625.
15625 = 625 x 25 + 0
So, HCF of 1250, 9375 and 15625 = 625
∴ The largest number that divides 1251, 9377 and 15628 leaving remainders 1, 2 and 3 respectively is 625.

Answer:

Answer:

12ⁿ can be written as (2² x 3)ⁿ = 2²ⁿ x 3ⁿ. We know that any number can end with the digit 0 or 5 only if its factor are 5 and 2. ∴ 12ⁿ cannot end at 0 or 5.

Answer:

Measures of steps of three persons are 40 cm, 42 cm and 45 cm, respectively.
If they have to cover same distance in complete steps.
We have to find LCM of their measures of steps.
LCM of 40, 42 and 45
Now, 40 = 2³ x 5
42 = 2 x 3 x 7
45 = 3² x 5
∴ LCM of 40, 42 and 45
= 2³ x 3² x 5 x 7 = 2520
∴ The distance they cover in complete steps
= 2520 cm = 25 m 20 cm.

Answer:

Answer:

Answer:

All positive integers can be written in the form of 6n + k, where n is any positive integer and k can be any integer 0, 1, 2, 3, 4, 5.
Now, the number can be written as 6n, 6n + 1,
6n + 2, 6n + 3, 6n + 4, 6n + 5.
∴ (6n)³ = 216n³ = 6(36n³)
= 6q + 0, where q = 36n³ and r = 0
(6n + 1)³ = 216n³ + 108n² + 18n + 1
= 6(36n³ + 18n² + 3n) + 1
= 6q + 1, where q = 36n³ + 18n² + 3n and r = 1
(6n + 2)³ = 216n³ + 216n² + 72n + 8
= 216n³ + 216n² + 72n + 6 + 2
= 6(36n³ + 36n² + 12n + 1) + 2
= 6q + 2,
where q = 36n³ + 36n² + 12n + 1 and r = 2
(6n + 3)³ = 216n³ + 324n² + 162n + 27
= 216n³ + 324n² + 162n + 24 + 3
= 6(36n³ + 54n² + 27n + 4) + 3
= 6q + 3,
where q = 36n³ + 54n² + 27n + 4 and r = 3
(6n + 4)³ = 216n³ + 432n² + 288n + 64
= 216n³ + 432n² + 288n + 60 + 4
= 6(36n³ + 72n² + 48n + 10) + 4
= 6q + 4,
where q = 36n³ + 72n² + 48n + 10 and r = 4
(6n + 5)³ = 216n³ + 540n2 + 450n + 125
= 216n³ + 540n² + 450n + 120 + 5
= 6(36n³ + 90n² + 75n + 20) + 5
= 6q + 5,
where q = 36n³ + 90n² + 75n + 20 and r = 5
So, by replacing q by m we can get the number to written as 6m + 0, 6m + 1, 6m + 2, 6m + 3, 6m + 4 and 6m + 5.

Answer:

Let ‘a’ be any positive integer and b = 3
Using Euclid's Lemma,
a = 3 x q + r, 0 $\le$ r $<$ 3
Case I: r = 0
a = 3q
(a) n = 3q (divisible by 3)
(b) n + 2 = 3q + 2 (not divisible by 3)
(c) n + 4 = 3q + 4 = 3q + 3 + 1
= 3(q + 1) + 1 (not divisible by 3)
Case II: r = 1
a = 3q + 1
(a) n = 3q + 1 (not divisible by 3)
(b) n + 2 = 3q + 3
= 3(q + 1) (divisible by 3)
(c) n + 4 = 3q + 5
= 3q + 3 + 2
= 3(q + 1) + 2 (not divisible by 3)
Case III: r = 2
a = 3q + 2
(a) n = 3q + 2 (not divisible by 3)
(b) n = 3q + 4
= 3q + 3 + 1
= 3(q + 1) + 1 (not divisible by 3)
(c) n = 3q + 6
= 3(q + 2), (divisible by 3)
So, it is clearly seen that only one out of n, n + 2,
n + 4 is divisible by 3 for a positive integer ‘n’.

Answer:

Let the 3 consecutive integers are n, n + 1, n + 2.
Let ‘a’ be any positive integer and b = 3.
Using Euclid‘s Lemma,
a = b x q + r 0 ≤ r < b
Case I: r = 0
a = 3q
(a) n = 3q (divisible by 3)
(b) n + 1 = 3q + 1 (not divisible by 3)
(c) n + 2 = 3q + 2 (not divisible by 3)
Case II: r = 1
a = 3q + 1
(a) n = 3q + 1 (not divisible by 3)
(b) n + 1 = 3q + 2 (not divisible by 3)
(c) n + 2 = 3q + 3
= 3(q + 1) (divisible by 3)
Case III: r = 2
a = 3q + 2
(a) n = 3q + 2 (not divisible by 3)
(b) n + 1 = 3q + 3
= 3(q + 1) (divisible by 3)
(c) n + 2 = 3q + 4
= 3(q + 1) + 1 (not divisible by 3)

Answer:

Here, n³ - n = n(n² - 1)
= n(n - 1) (n + 1),
which is three consecutive integers.
Let ‘a’ be any positive integer and b = 6
Using Euclid’s Lemma,
a = b x q + r, 0 $\le$ r $<$ b
Case I: r = 0
∴ a = 6q
n³ - n = n(n - 1) (n + 1)
= 6q(6q - 1) (6q + 1) (divisible by 6)
Case II: r = 1
∴ a = 6q + 1
n³ - n = n(n - 1) (n + 1)
= (6q + 1) (6q + 1 - 1) (6q + 1 + 1)
= (6q + 1) (6q) (6q + 2)
(divisible by 6)
Case III: r = 2
∴ a = 6q + 2
n³ - n = (n) (n - 1) (n + 1)
= (6q + 2) (6q + 2 - 1) (6q + 2 + 1)
= (6q + 2) (6q + 1) (6q + 3)
= 2(3q + 1) (6q + 1) 3(2q + 1)
= 6(3q + 1) (6q + 1) (2q + 1)
(divisible by 6)
Case IV: r = 3
n³ - n = n(n - 1) (n + 1)
= (6q + 3) (6q + 3 - 1) (6q + 3 + 1)
= 3(2q + 1) (6q + 2) (6q + 4)
= 6(2q + 1)(3q + 1)(6q + 4)
(divisible by 6)
Case V: r = 4
n³ - n = n(n - 1) (n + 1)
= (6q + 4) (6q + 4 - 1) (6q + 4 + 1)
= 2(3q + 2) (6q + 3) (6q + 5)
= 6(3q + 2) (2q + 1) (6q + 5)
(divisible by 6)
Case VI: r = 5
n³ - n = n(n - 1) (n + 1)
= (6q + 5) (6q + 5 - 1) (6q + 5 + 1)
= (6q + 5) (6q + 4) (6q + 6)
= 6(6q + 5) (6q + 4) (q + 1)
(divisible by 6)

Answer:

Let a be any positive integer.
So, a can be written as 5q, 5q + 1, 5q + 2, 5q + 3,
5q + 4 for some integer q.
Suppose, n = 5q (divisible by 5)
n + 4 = 5q + 4 (not divisible by 5)
n + 8 = 5q + 8
= 5q + 5 + 3
= 5(q + 1) + 3 (not divisible by 5)
n + 12 = 5q + 12 = 5q + 10 + 2
= 5(q + 2) + 2 (not divisible by 5)
n + 16 = 5q + 16 = 5q + 15 + 1
= 5(q + 3) + 1 (not divisible by 5)
Suppose, n = 5q + 1
∴ n = 5q + 1 (not divisible by 5)
n + 4 = 5q + 1 + 4 = 5q + 5
= 5(q + 1) (divisible by 5)
n + 8 = 5q + 1 + 8 = 5q + 9
= 5q + 5 + 4
= 5(q + 1) + 4 (not divisible by 5)
n + 12 = 5q + 1 + 12 = 5q + 13
= 5q + 10 + 3
= 5(q + 2) + 3 (not divisible by 5)
n + 16 = 5q + 1 + 16 = 5q + 17
= 5q + 15 + 2
= 5(q + 3) + 2 (not divisible by 5) Suppose, n = 5q + 2 ∴ n = 5q + 2 (not divisible by 5)
n + 4 = 5q + 6
= 5(q + 1) + 1 (not divisible by 5)
n + 8 = 5q + 10
= 5(q + 2) (divisible by 5)
n + 12 = 5q + 14
= 5(q + 2) + 4 (not divisible by 5)
n + 16 = 5q + 18
= 5(q + 3) + 3 (not divisible by 5)
Suppose, n = 5q + 3
∴ n = 5q + 3 (not divisible by 5)
n + 4 = 5q + 7
= 5(q + 1) + 2 (not divisible by 5)
n + 8 = 5q + 11
= 5(q + 2) + 1 (not divisible by 5)
n + 12 = 5q + 15
= 5(q + 3) (divisible by 5)
n + 16 = 5q + 19
= 5(q + 3) + 4 (not divisible by 5)
Suppose, n = 5q + 4
∴ n = 5q + 4 (not divisible by 5)
n + 4 = 5q + 8
= 5(q + 1) + 3 (not divisible by 5)
n + 8 = 5q + 12
= 5(q + 2) + 2 (not divisible by 5)
n + 12 = 5q + 16
= 5(q + 3) + 1 (not divisible by 5)
n + 16 = 5q + 20
= 5(q + 4) (divisible by 5)
So, one and only one out of n, n + 4, n + 8, n + 12 and n + 16 is divisible by 5.