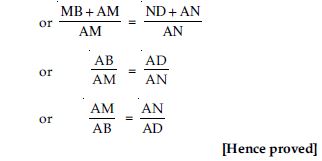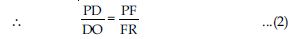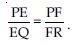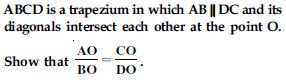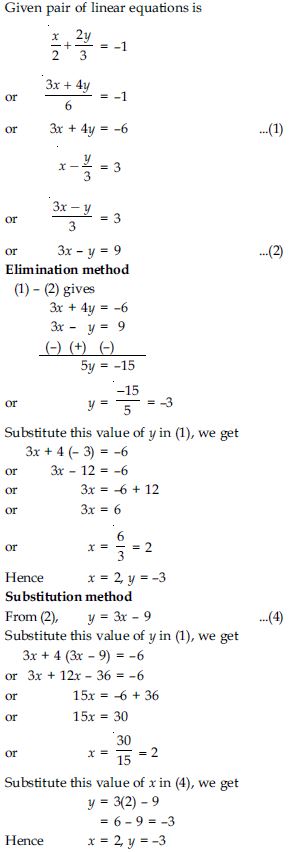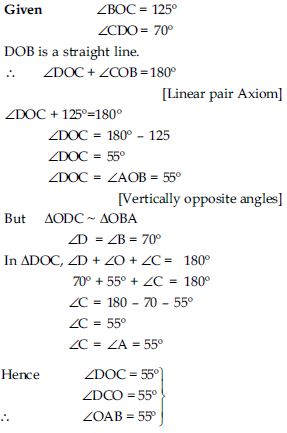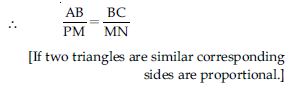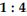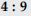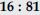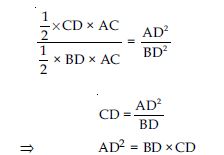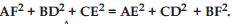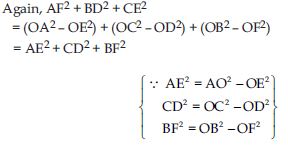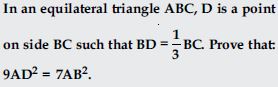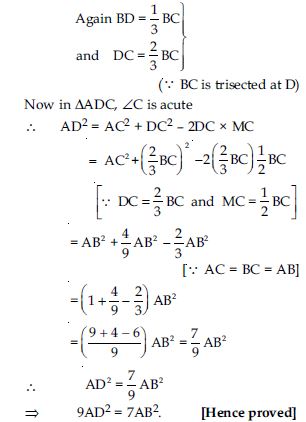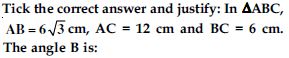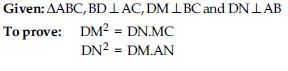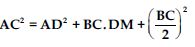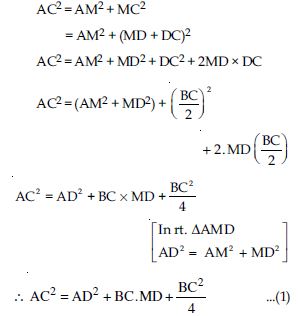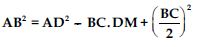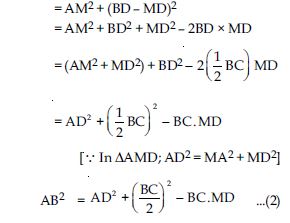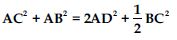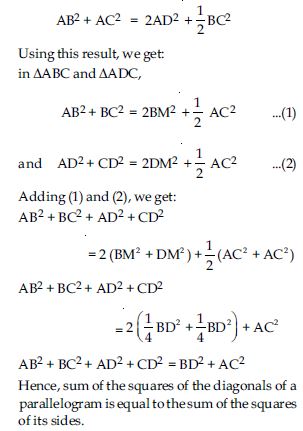Aasoka has some of the top educational resources for the students of Class 10th. So, students can get free access to NCERT Solutions to help students boost their preparations for board exams. The solutions will benefit students in every step of the preparation. The topics can be clearly understood through this, revision can be done easily, and so much more. NCERT Solutions for Class 10th are an excellent way to revise the entire chapter for better understanding. The team of experts has made sure to include the latest syllabus questions and frame their answers accordingly.
“Triangles” chapter of Class 10th Math will teach students about the different types of triangles. It begins with the explanation of a congruent and simple figure. The chapter describes the condition for the similarity of 2 triangles and the theorems which are based on it. Then, with the help of a theorem, areas of similar triangles are explained. In the end, the chapter describes the Pythagoras Theorem and the converse of the Pythagoras Theorem.
Question 1:
All circles are ________. (congruent, similar)
Answer:
similar
Question 2:
All squares are ________. (similar, congruent)
Answer:
similar
Question 3:
All ________ triangles are similar. (isosceles, equilateral)
Answer:
equilateral
Question 4:
Two polygons of the same number of sides are similar, if their corresponding angles are ________ and their corresponding sides are ________. (equal, proportional)
Answer:
equal, proportional
Question 5:
Give two different examples of a pair of: similar figures
Answer:
(a) Pair of equilateral triangles are similar figures.
(b) Pair of squares are similar figures.
Question 6:
Give two different examples of a pair of: non-similar figures.
Answer:
(a) A triangle and quadrilateral form a pair of non-similar figures.
(b) A square and rhombus form pair of non-similar figures.
Question 7:
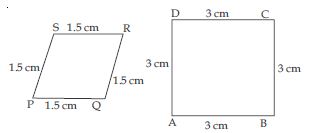
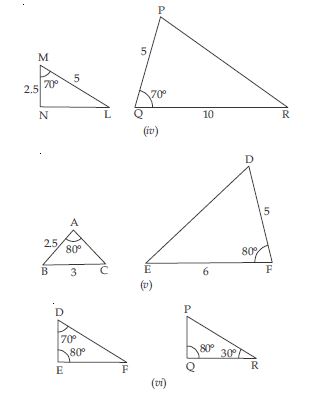
State whether the following quadrilaterals are similar or not:
Answer:
The two quadrilaterals in the figure are not similar because their corresponding angles are not equal.
Question 8:
E and F are points on the sides PQ and PR
respectively of a PQR. For each of the
following cases, state whether EF || QR:
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and
FR = 2.4 cm
Answer:
In PQR, E and F are two points on side PQ and PR respectively.
Question 9:
E and F are points on the sides PQ and PR respectively of a PQR. For each of the following cases, state whether EF || QR: PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Answer:
In PQR, E and F are two points on side PQ and PR respectively.
Question 10:
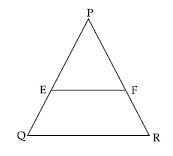
E and F are points on the sides PQ and PR respectively of a PQR. For each of the following cases, state whether EF || QR: PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Answer:
In PQR, E and F are two points on side PQ and PR respectively.
PQ = 1.28 cm, PR = 2.56 cm
PE = 0.18 cm, PF = 0.36 cm.
EQ = PQ - PE = 1.28 - 0.18 = 1.10 cm
FR = PR - PF = 2.56 - 0.36 = 2.20 cm
Question 11:
Answer:
Question 12:
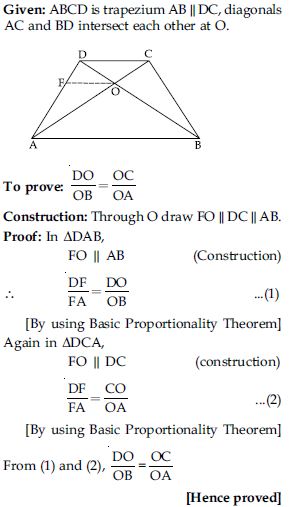
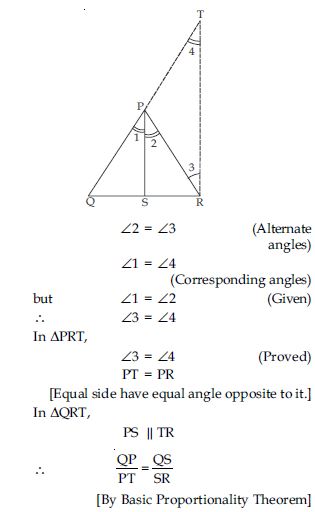
In fig. DE || OQ and DF || OR. Show that EF || QR.
Answer:
Given: PQR, DE || OQ
DF || OR
To prove: EF || QR.
Proof: In PQO,
ED || QO (given)
[By Basic Proportionality Theorem]
Again in POR,
DF || OR (given)
[By Basic Proportionality Theorem]
From (1) and (2),
In PQR, by using converse of Basic
Proportionality Theorem.
EF || QR
[Hence proved]
Question 13:
In fig., A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
Answer:
Given: PQR, A, B and C are points on OP,
OQ and OR respectively such that
AB || PQ, AC || PR
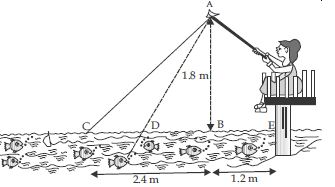
Question 14:
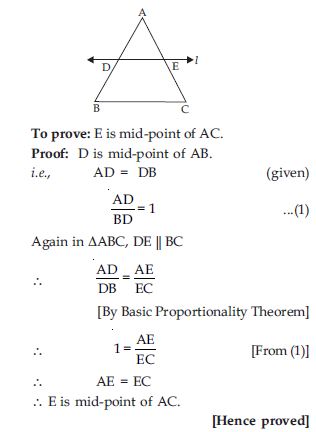
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Answer:
Given: ABC, D is mid-point of AB, i.e.,
AD = DB.
A line parallel to BC intersects AC at E as
shown in figure, i.e., DE || BC.
Question 15:
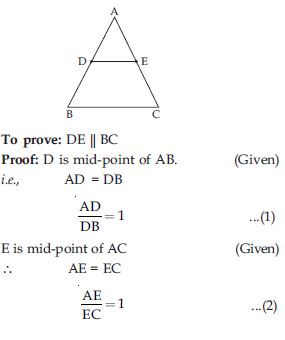
Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Answer:
Given: ABC, D and E are mid-points of AB and AC respectively such that AD = DB and AE = EC, D and E are joined.
Question 16:
Answer:
Question 17:
Answer:
Question 18:
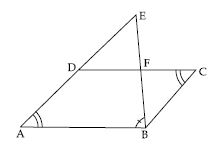
State which pairs of triangles in fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
Answer:
Question 19:
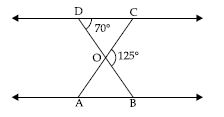
In fig., ODC ~ OBA, BOC = 125 and
CDO = 70º. Find DOC, DCO and
OAB.
Answer:
Question 20:
Answer:
Question 21:
Answer:
Question 22:
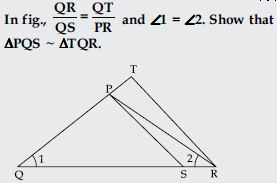
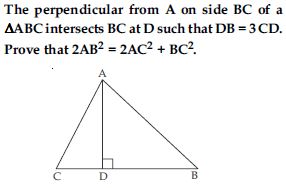
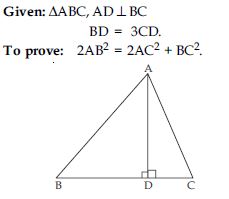
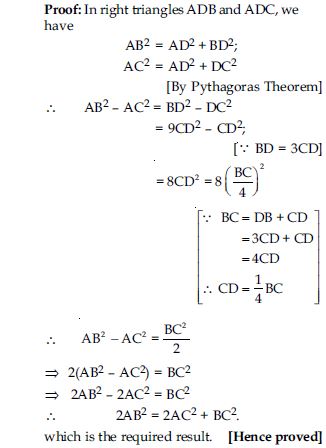
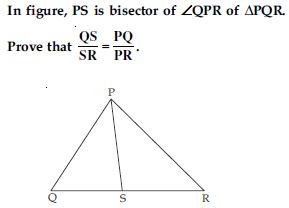
S and T are points on sides PR and QR of PQR such that P = RTS. Show that RPQ ~ RTS.
Answer:
PQR, S and T are points on side PR and QR such that P = RTS
To prove: RPQ ~ RTS
Proof: In RPQ and RTS
RPQ = RTS (given)
R = R [common angles]
∴ RPQ ~ RTS [By AA similarity criterion]
Question 23:
In figure, if ABE ACD, show that ADE ~ ABC
Answer:
Question 24:
In fig., altitudes AD and CE of ABC intersect
each other at the point P. Show that:
(i) AEP ~ CDP
(ii) ABD ~ CBE
(iii) AEP ~ ADB
(iv) PDC ~ BEC
Answer:
Question 25:
E is a point on the side AD produced by a parallelogram ABCD and BE intersects CD at F. Show that ABE ~ CFB.
Answer:
Given: Parallelogram ABCD. Side AD is
produced to E, BE intersects DC at F
To prove: ABE ~ CFB
Proof: In ABE and CFB.
A = C
(Opposite angles of ||gm)
ABE = CFB (Alternate angles)
∴ ABE ~ CFB
(AA similarity criterion)
Question 26:
Answer:
Question 27:
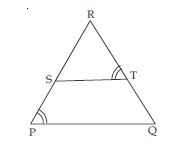
CD and GH are respectively the bisectors of ACB and EGF such that D and H lie on sides AB and FE of ABC and EFG respectively. If ABC ~ FEG, show that:
Answer:
Given: In ABC and EFG, CD and GH are bisectors of ACB and EGF
Question 28:
In fig., E is a point on side CB produced of
an isosceles triangle ABC with AB = AC.
If AD BC and EF AC, prove that ABD
~ ECF.
Answer:
Given: ABC, isosceles triangle with AB = AC
AD BC, side BC is produced to E. EF AC
To prove: ABD ~ ECF
Proof: ABC is isosceles
AB = AC (given)
∴ B = C
[Equal sides have equal angles opposite to it.]
In ABD and ECF,
ABD = ECF (Proved above)
ADB = EFC (each 90)
∴ ABD ~ ECF [AA similarity]
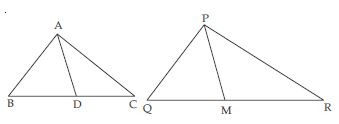
Question 29:
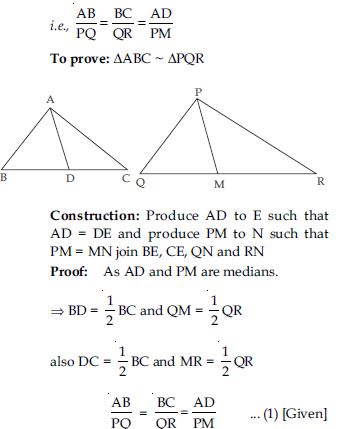
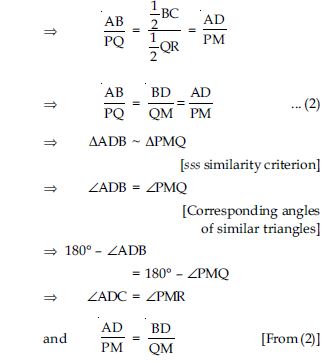
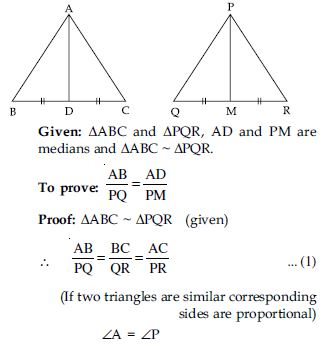
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of PQR (see fig.). Show that ABC ~ PQR.
Answer:
Given: ABC and PQR, AB, BC, and median AD of ABC are proportional to side PQ, QR and median PM of PQR,
Question 30:
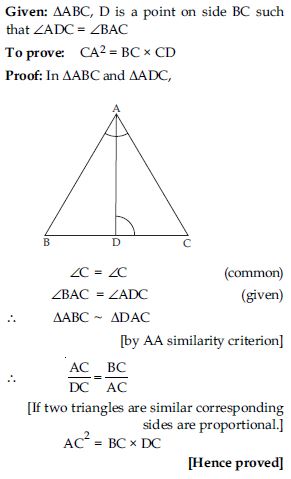
D is a point on the side BC of a triangle
ABC such that ADC = BAC. Show that
CA2 = CB . CD.
Answer:
Question 31:
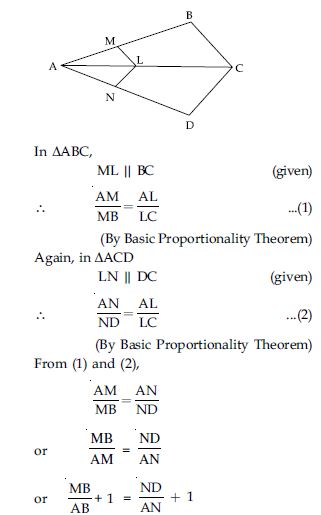
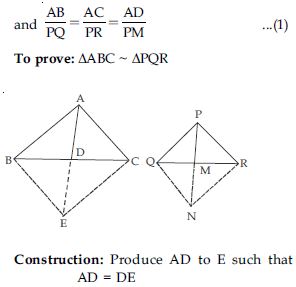
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ABC ~ PQR.
Answer:
Given: Two s ABC and PQR. D is the midpoint of BC and M is the mid-point of QR.
Join BE and CE.
Produce PM to N such that PM = MN.
Join QN and NR.
Proof: In quad. ABEC, diagonals AE and BC
bisect each other at D.
∴ Quad. ABEC is a parallelogram.
Similarly, it can be shown that quad. PQNR is
a parallelogram.
Since ABEC is a parallelogram
∴ BE = AC ...(2)
Similarly, since PQNR is a || gm
∴ QN = PR ...(3)
Dividing (2) by (3), we get:
Question 32:
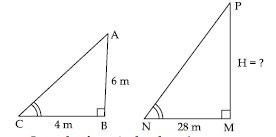
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Answer:
Length of vertical pole = 6 m
Shadow of pole = 4 m
Let height of tower be H m
Length of shadow of tower = 28 m
In ABC and PMN,
C = N
(Angle of altitude of sun at same time)
B = M (each 90)
∴ ABC ~ PMN
[AA similarity criterion]
Question 33:
Answer:
Question 34:
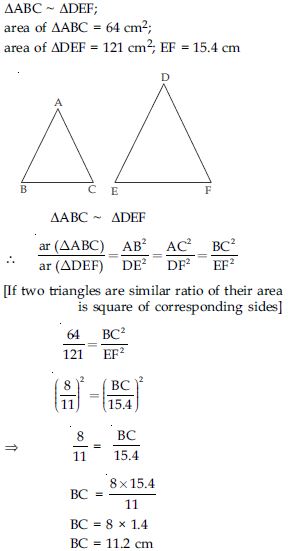
Let ABC ~ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Answer:
Question 35:
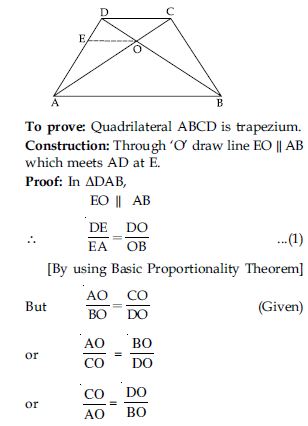
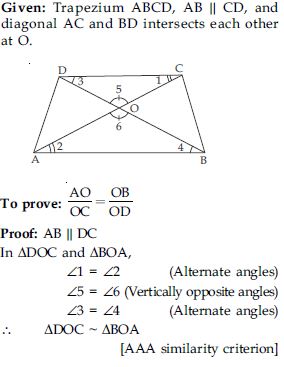
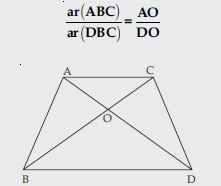
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Answer:
ABCD is trapezium AB || DC. Diagonals AC and BD intersects each other at the point O. AB = 2 CD
Question 36:
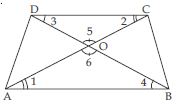
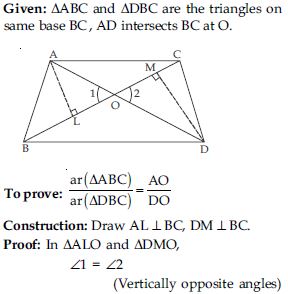
In fig., ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that:
Answer:
Question 37:
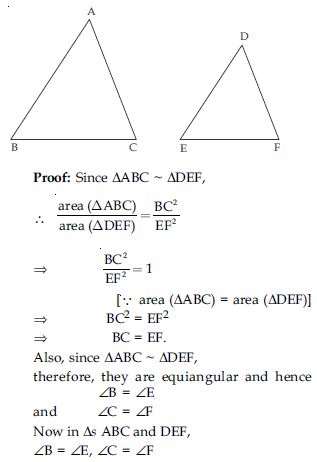
If the areas of two similar triangles are equal, prove that they are congruent.
Answer:
Given: Two s ABC and DEF are similar and equal in area. To prove: ABC DEF
and BC = EF ∴ ABC DEF (ASA congruence)
Question 38:
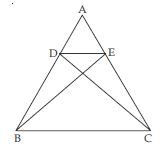
D, E and F are respectively the mid-points of the sides AB, BC and CA of ABC. Find the ratio of the areas of DEF and ABC.
Answer:
(SSS congruency Theorem)
Similary, we can prove that:
CFE DEF
and EDB DEF
If s are congruent, then they are equal in area.
∴ ar(FAD) = ar(DEF) ...(1)
ar(CFE) = ar(DEF) ...(2)
ar(EDB) = ar(DEF) ...(3)
Now ar (ABC)
= ar(FAD) + ar(DEF)
+ ar(CFE) + ar(EDB)
= ar(DEF) + ar(DEF)
Question 39:
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Answer:
Given: ABC ~ DEF.
AX and DY are the medians to the side BC
and EF respectively.
[Hence proved]
Question 40:
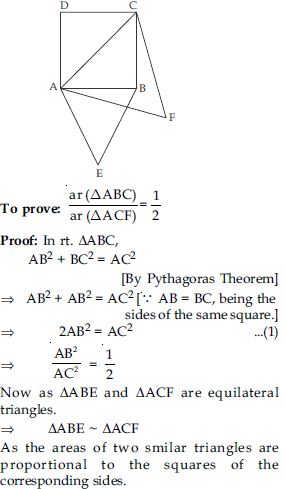
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Answer:
Given: ABCD is a square. Equilateral ABE is described on the side AB of the square and equilateral ACF is described on the diagonal AC.
Question 41:
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
Answer:
(iii)
Question 42:
Sides of two similar triangles are in the ratio
4 : 9. Areas of these triangles are in the ratio
Answer:
(iv)
Question 43:
Sides of triangles are given below. Determine which of them are right triangles. In case of a
right triangle, write the length of its hypotenuse.
7 cm, 24 cm, 25 cm
Answer:
Question 44:
Sides of triangles are given below. Determine which of them are right triangles. In case of a
right triangle, write the length of its hypotenuse.
3 cm, 8 cm, 6 cm
Answer:
Question 45:
Sides of triangles are given below. Determine which of them are right triangles. In case of a
right triangle, write the length of its hypotenuse.
50 cm, 80 cm, 100 cm
Answer:
Question 46:
Sides of triangles are given below. Determine which of them are right triangles. In case of a
right triangle, write the length of its hypotenuse.
13 cm, 12 cm, 5 cm.
Answer:
Question 47:
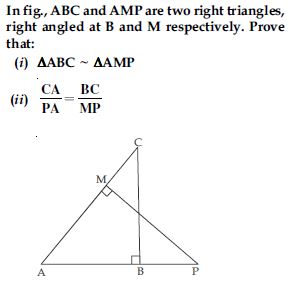
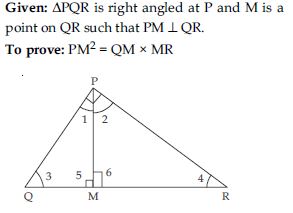
PQR is a triangle right angled at P and M is a point on QR such that PM QR. Show that PM2 = QM.MR.
Answer:
Question 48:
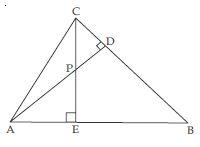
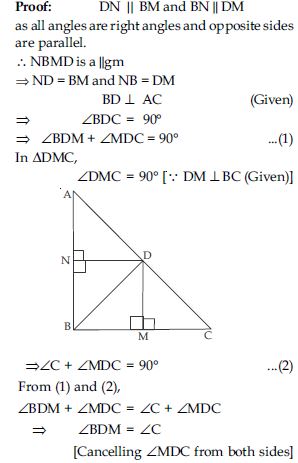
In fig., ABD is a triangle right angled at A and AC BD. Show that:
AB2= BC.BD
Answer:
Question 49:
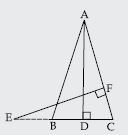
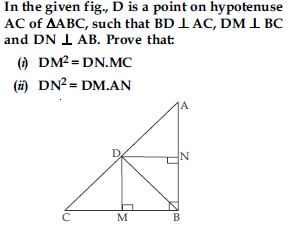
In fig., ABD is a triangle right angled at A and AC BD. Show that:
<img height="218" src= "images/MBD NCERT Solution_Math_G10 (E)_Img 553.jpg" width="360">
AC2 = BC.DC
Answer:
Question 50:
In fig., ABD is a triangle right angled at A and AC BD. Show that:
AD2 = BD.CD
Answer:
Question 51:
ABC is an isosceles triangle right angled at C.
Prove that AB2 = 2AC2.
Answer:
Question 52:
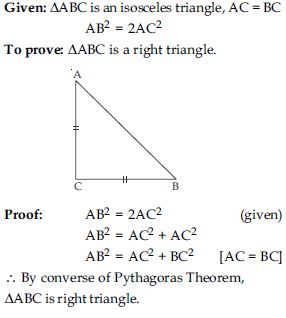
ABC is an isosceles triangle with AC = BC.
If AB2 = 2AC2, prove that ABC is right triangle.
Answer:
Question 53:
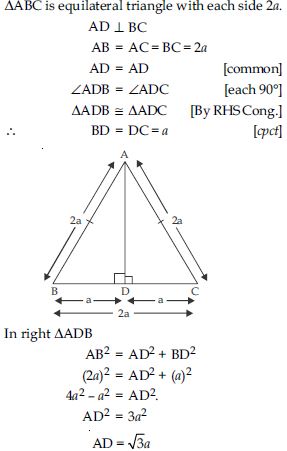
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Answer:
Question 54:
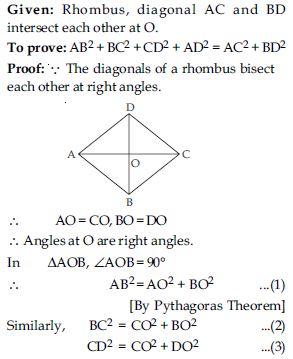
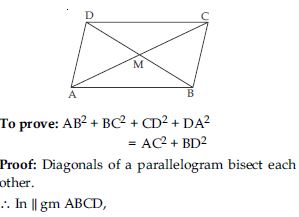
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Answer:
Question 55:
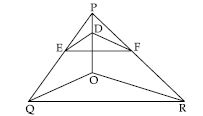
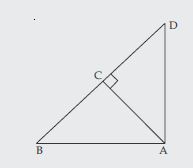
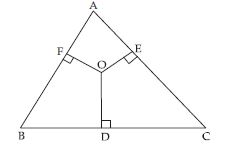
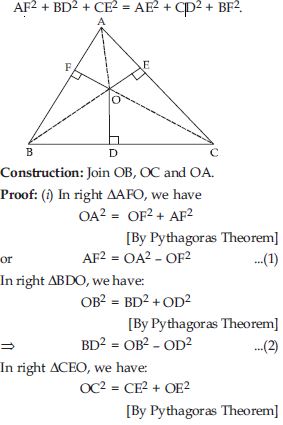
In fig., O is a point in the interior of a triangle ABC, OD BC, OE AC and OF AB. Show that:
Answer:
Question 56:
In fig., O is a point in the interior of a triangle ABC, OD BC, OE AC and OF AB. Show that:
Answer:
Question 57:
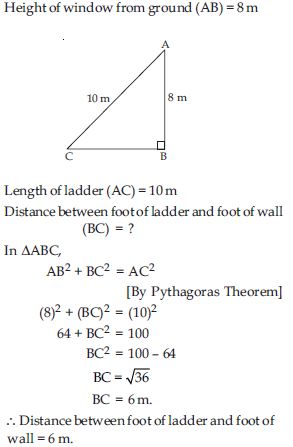
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Answer:
Question 58:
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Answer:
Let AB is height of pole (AB) = 18 m
AC is length of wire = 24 m
Question 59:
Answer:
Question 60:
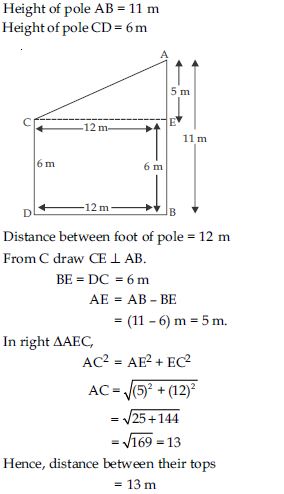
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Answer:
Question 61:
D and E are points on the sides CA and CB
respectively of a triangle ABC right angled
at C.
Prove that AE2 + BD2 = AB2 + DE2.
Answer:
Given: ABC is right angled at C, D and E are
point on CA and BC respectively.
Question 62:
Answer:
Question 63:
Answer:
Question 64:
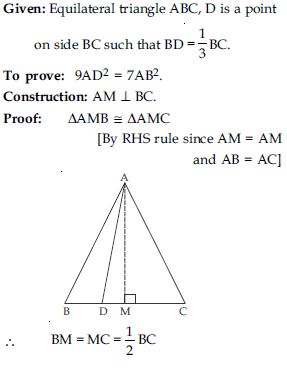
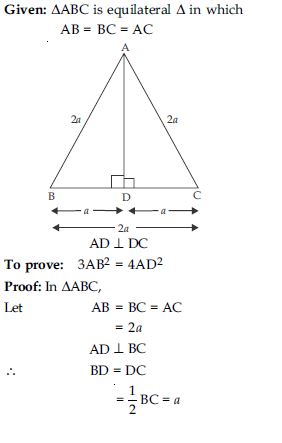
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Answer:
Question 65:
- 120
- 60
- 90
- 45
Answer:
(iii) 90
Question 66:
Answer:
Question 67:
Answer:
Question 68:
Answer:
Question 69:
Answer:
Question 70:
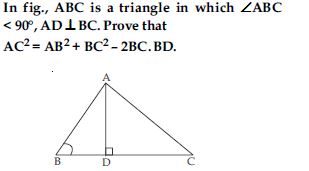
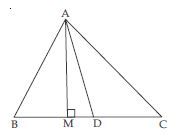
In fig., AD is a median of a triangle ABC and AM BC. Prove that:
Answer:
In AMC,
Question 71:
In fig., AD is a median of a triangle ABC and AM BC. Prove that:
Answer:
In right triangle AMB,
AB2=AM2 + BM2
Question 72:
In fig., AD is a median of a triangle ABC and AM BC. Prove that:
Answer:
which is the required result. [Hence proved]
Question 73:
Prove that sum of squares of the diagonals of a parallelogram is equal to sum of squares of its sides.
Answer:
Given: Let ABCD be a parallelogram in which diagonals AC and BD intersect at point M.
Diagonal BD and AC bisect each other.
Or MB and MD are medians of ABC and ADC
respectively.
As proved in Q.5. (iii)
We know that, if AD is a median of ABC, then
Question 74:
Answer:
Question 75:
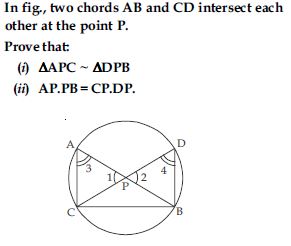
Answer:
[If two triangles are similar corresponding sides are proportional.]
PA × PB = PC × PD.
Question 76:
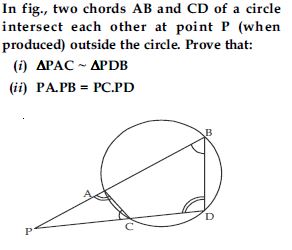
Answer:
Question 77:
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out? If she pulls in the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds?