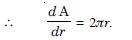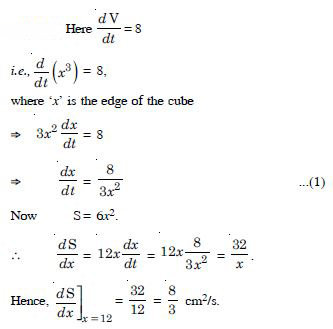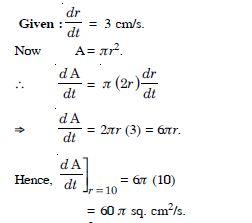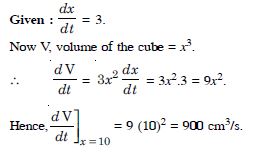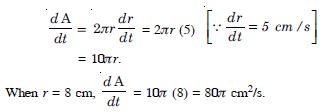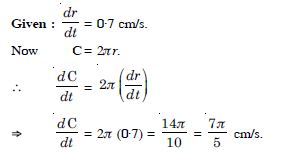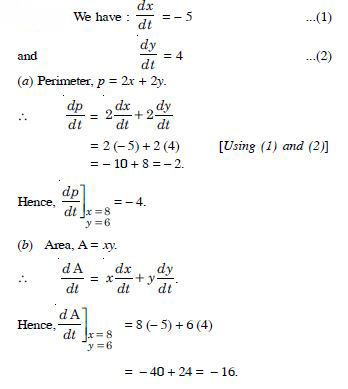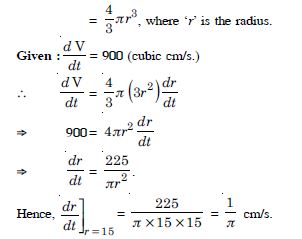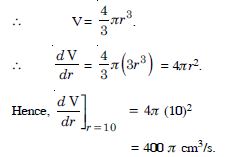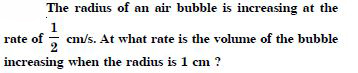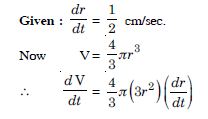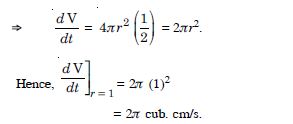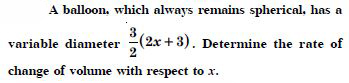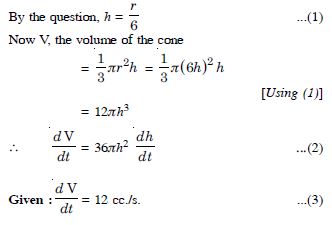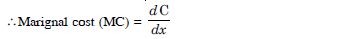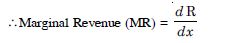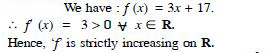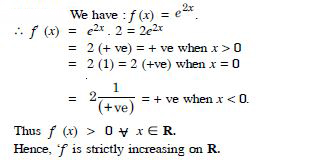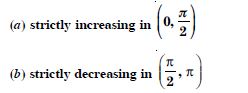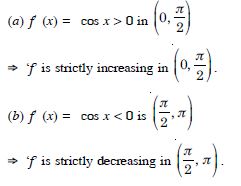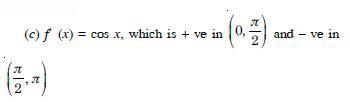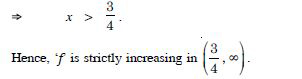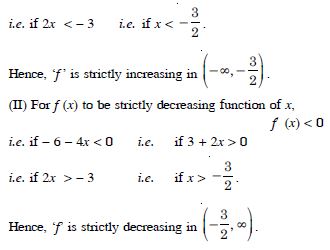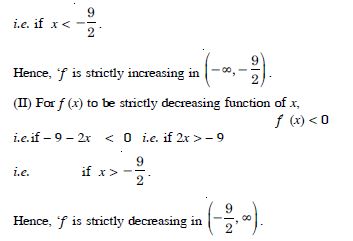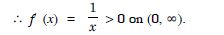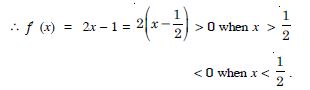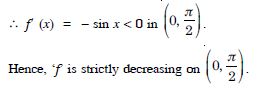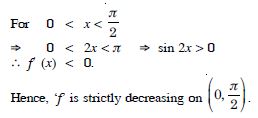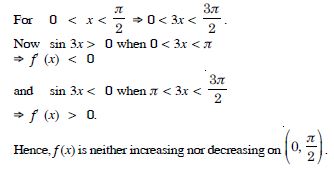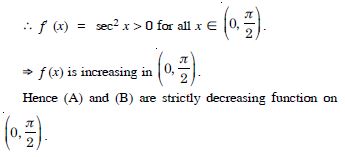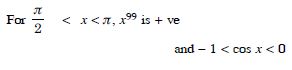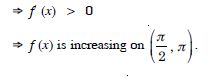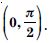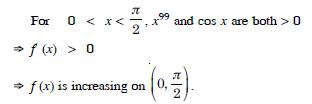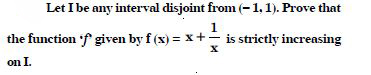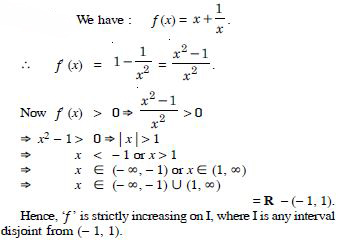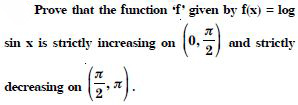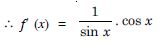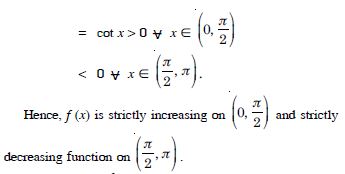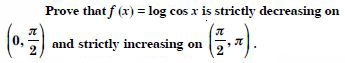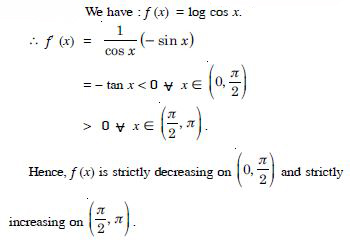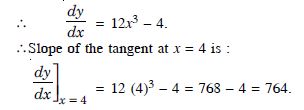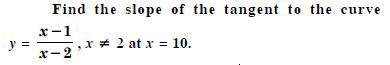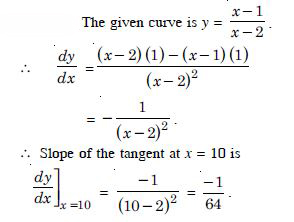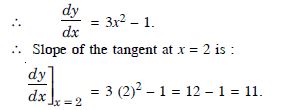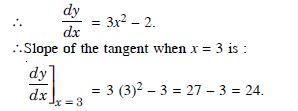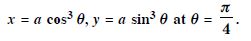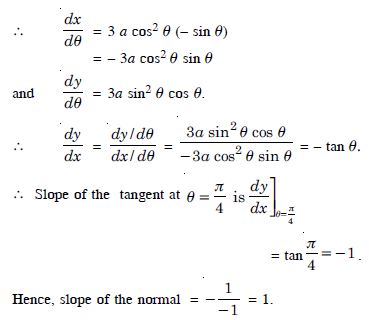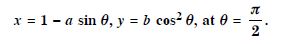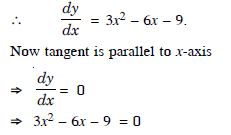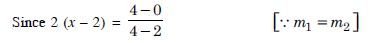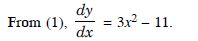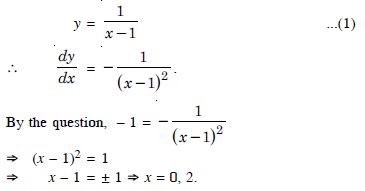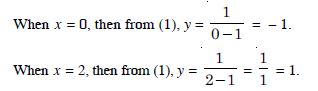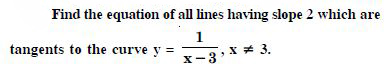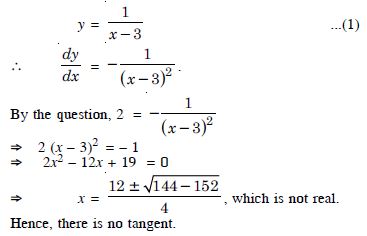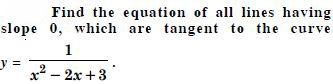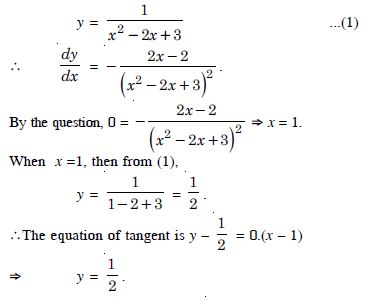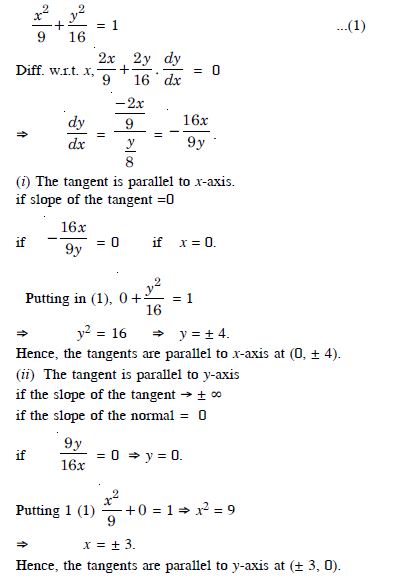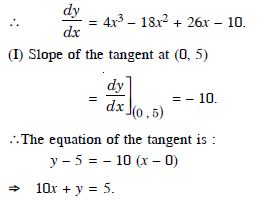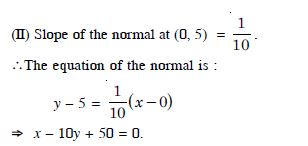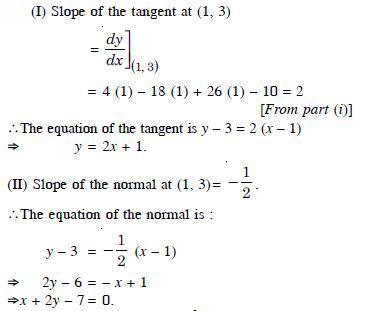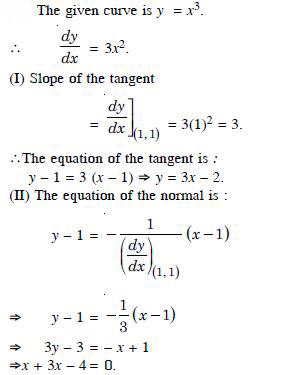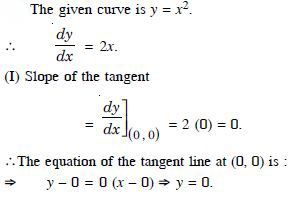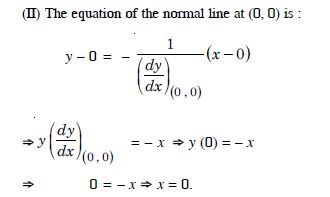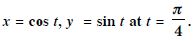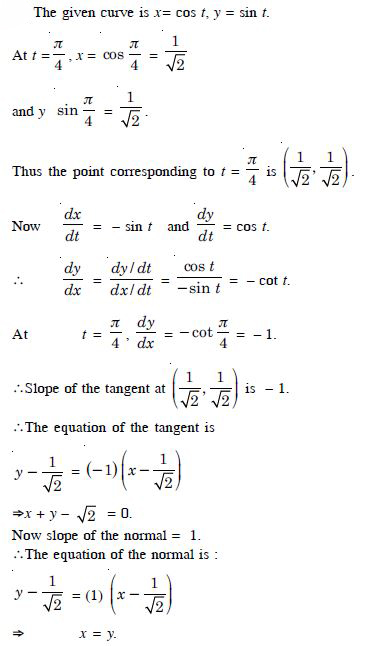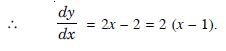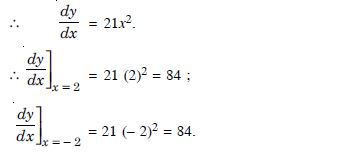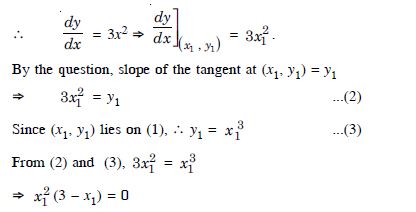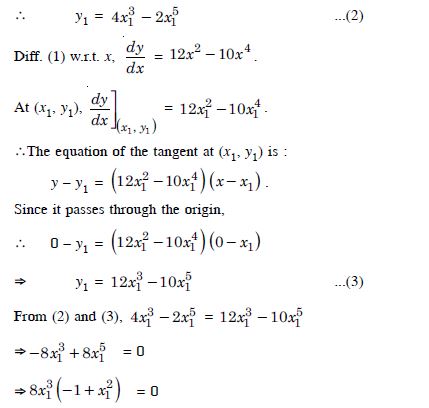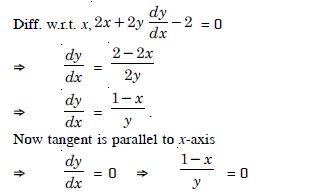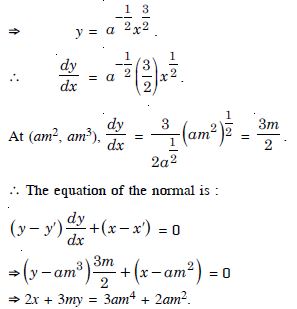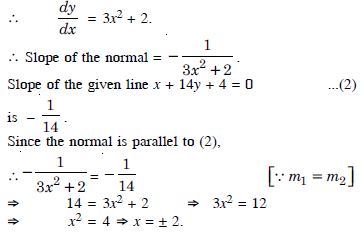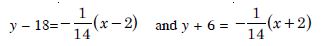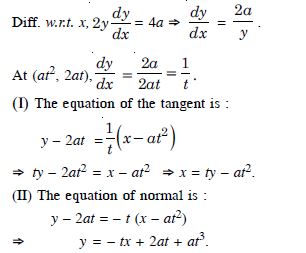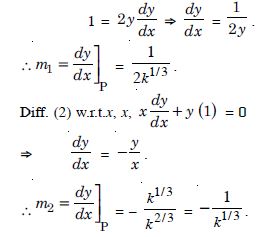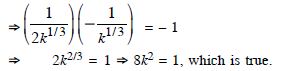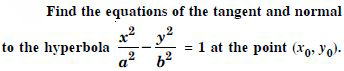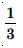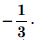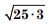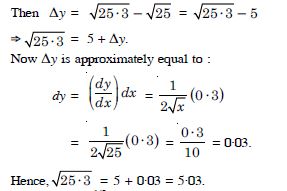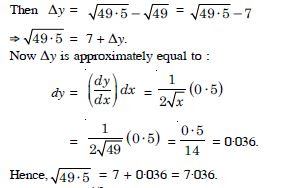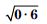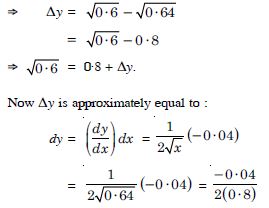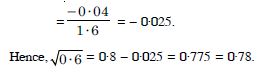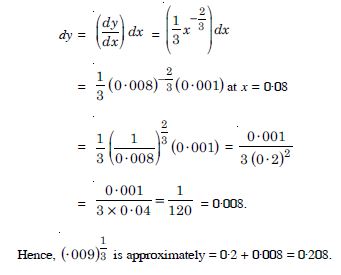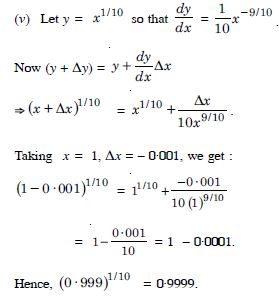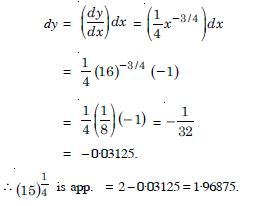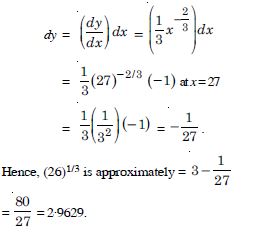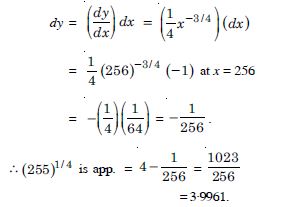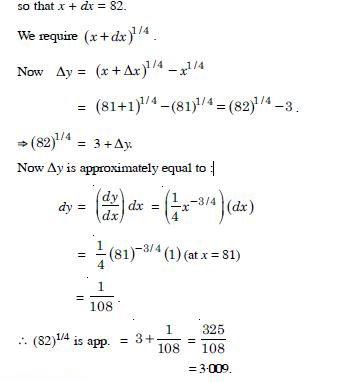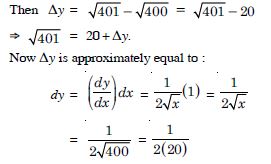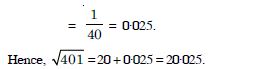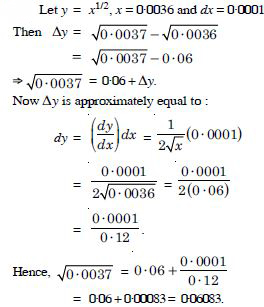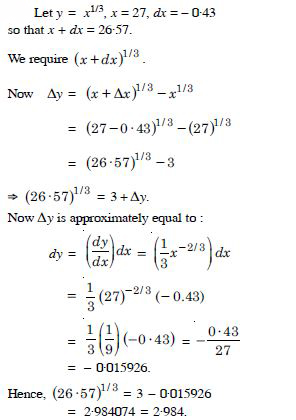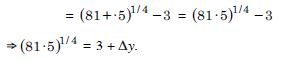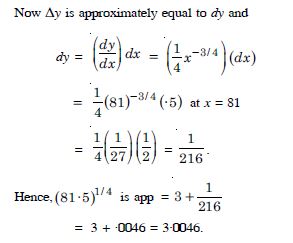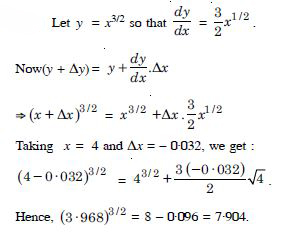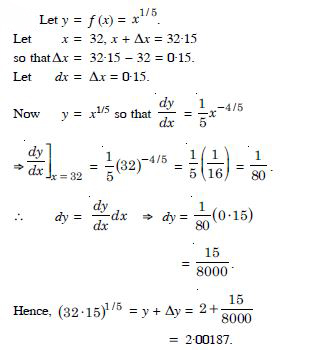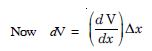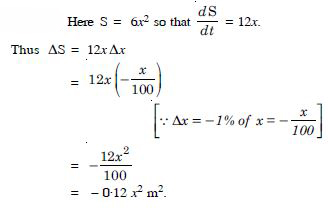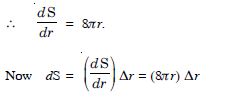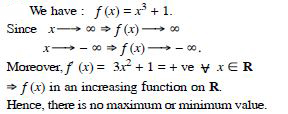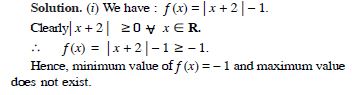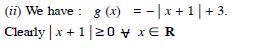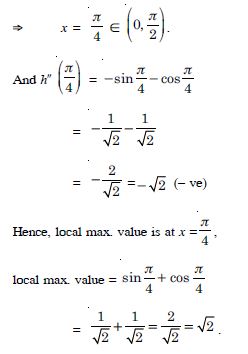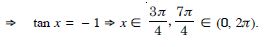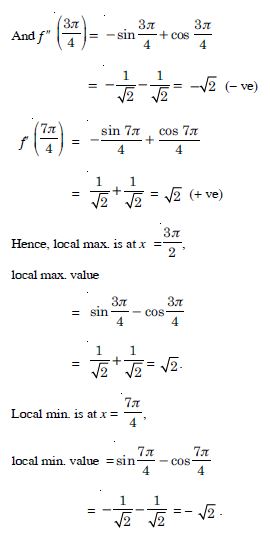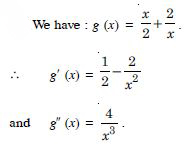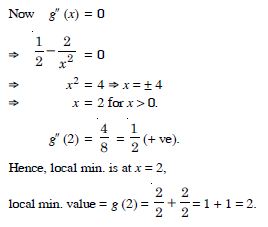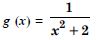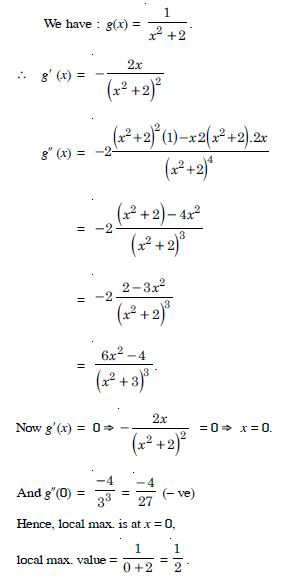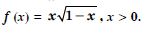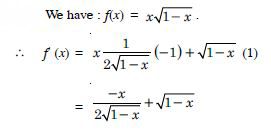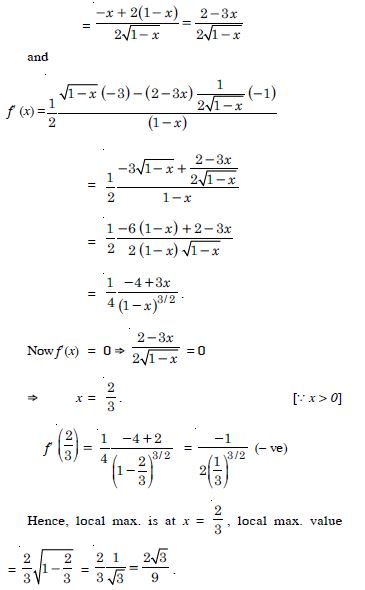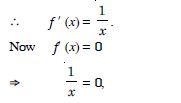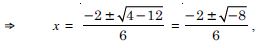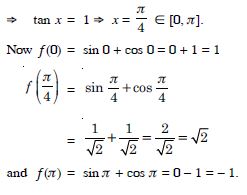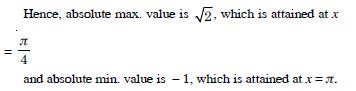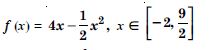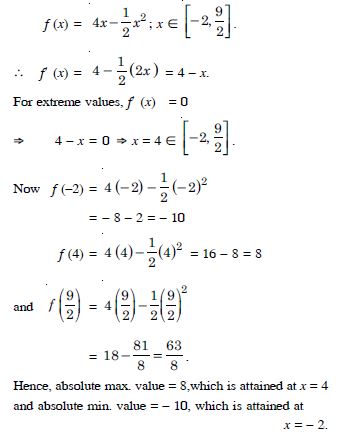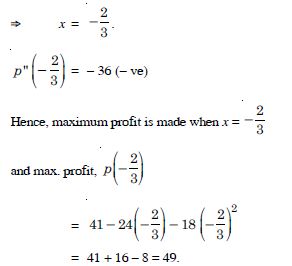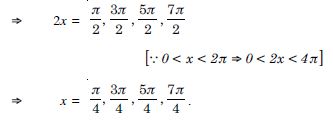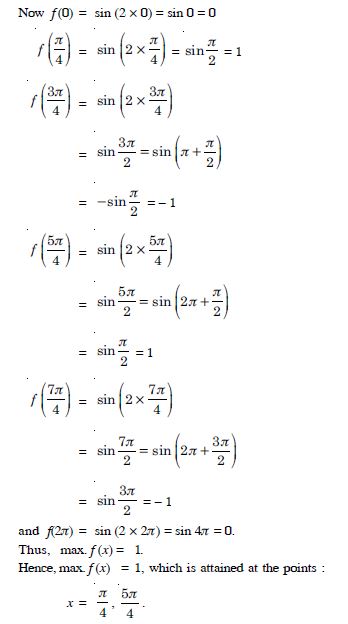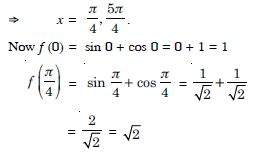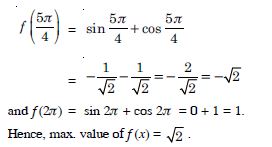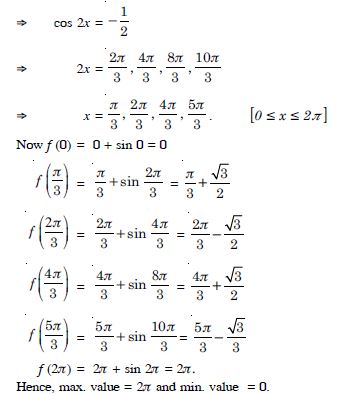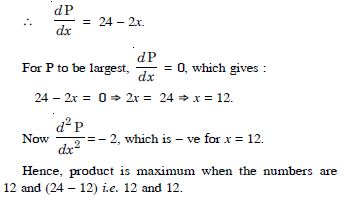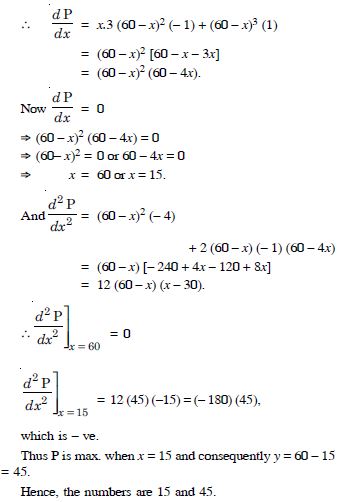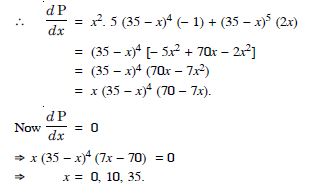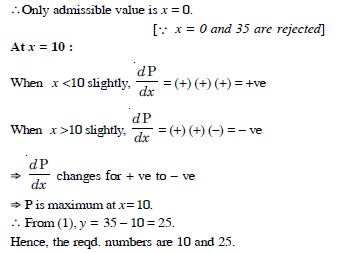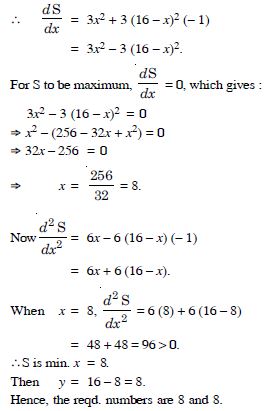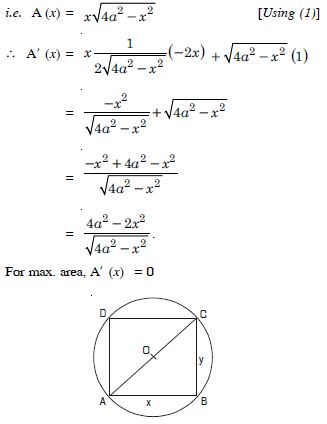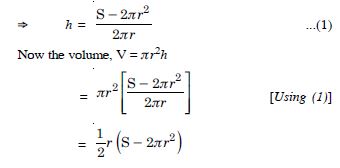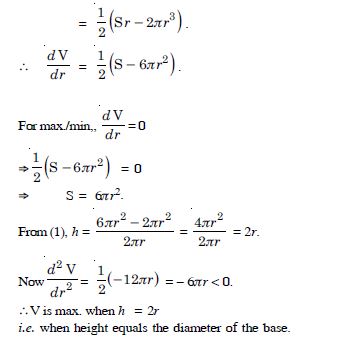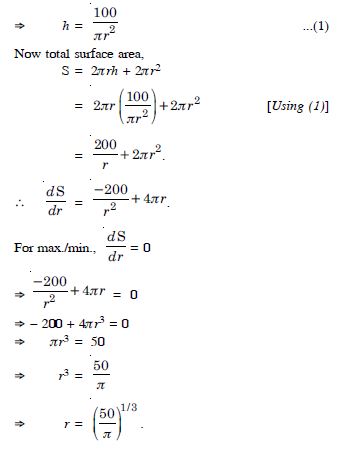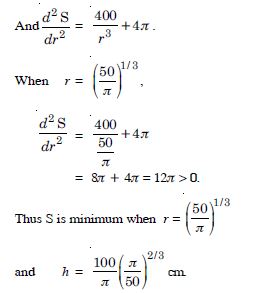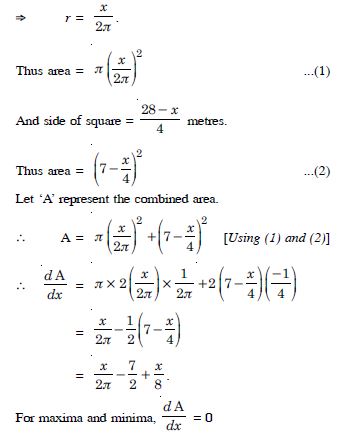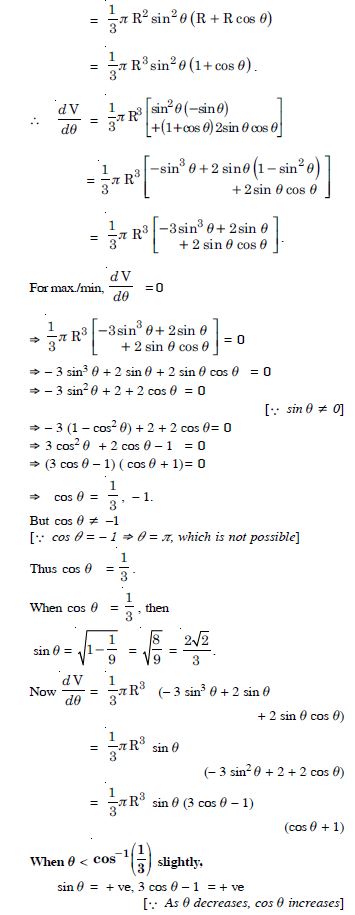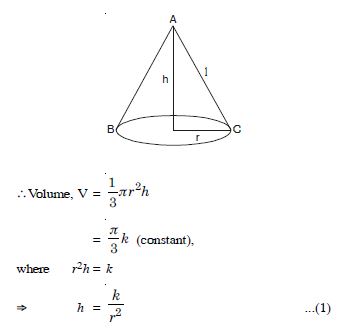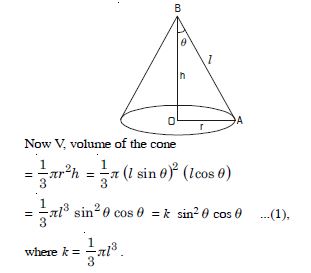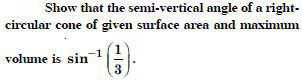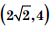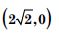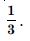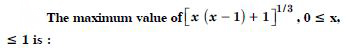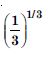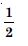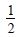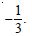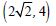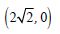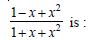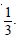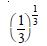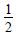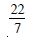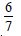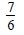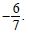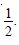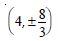Question 1:
Find the rate of change of the area of circle with respect to its radius r. How fast is the area changing with respect to the radius when :
(a) r = 3 cm (b) r = 4 cm.
Answer:
Let ‘r’ be the radius of the circle.
Then A, the area of the circle = r2.
Hence, the rate of change of the area of the circle = 2r.
(a) When r = 3 cm, then the rate of change of the area of the circle = 2 (3) = 6 cm2/s.
(b) When r = 4 cm, then the rate of change of the area of the circle = 2 (4) = 8 cm2/s.
Question 2:
The volume of a cube is increasing at the rate of 8 cm3/s. How fast is the surface area increasing when the length of the edge is 12 cm ?
Answer:
Question 3:
The radius of the circle is increasing uniformly at rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
Answer:
Question 4:
An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge is 10 cm long ?
Answer:
Let ‘x’ be the edge of the cube.
Question 5:
A stone is dropped into a quiet lake and waves move in circles at a speed of 5 cm. per second. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing ?
Answer:
Let ‘r’ be the radius of the circular wave.
Then A= r2,
where A is the enclosed area at time t.
Differentiating w.r.t. t, we get :
Hence, the enclosed area is increasing at the rate of 80 cm2/s, where r = 8 cm.
Question 6:
The radius of a circle is increasing at the rate of 0·7 cm/s. What is the rate of increasing of its circumference ?
Answer:
Let ‘r’ be the radius of the circle.
Question 7:
The length x of a rectangle is decreasing at the rate of 5 cm/minute and width y is increasing
at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of :
(a) the perimeter and (b) the area of the rectangle.
Answer:
Question 8:
A balloon, which always remains spherical, is being inflated by pumping in 900 cubic centimeters of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
Answer:
V, the volume of the balloon
Question 9:
A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the latter is 10 cm.
Answer:
Let ‘r’ be the variable radius of the balloon.
Question 10:
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 m/s. How fast is the height, on the wall decreasing when the foot of the ladder is 4 m away from the wall ?
Answer:
Let MP be the wall and AB = (5 m) be the
ladder.
Let BM = x metres.
Question 11:
A particle moves along the curve 6y = x3 + 2. Find the points on the curve at which the y-co-ordinate is changing 8 times as fast as the x-coordinate.
Answer:
We have :
Question 12:
Answer:
Let ‘r’ be the radius of the air bubble.
Question 13:
Answer:
Radius (say r) of sphere
Question 14:
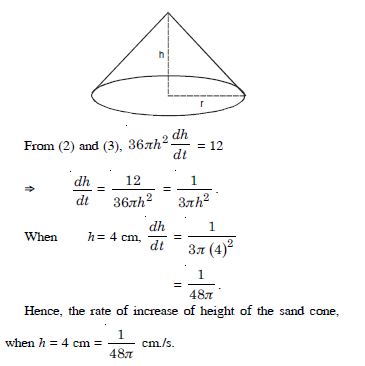
Sand is pouring from a pipe at the rate of 12 cc/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always onesixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm ?
Answer:
Let ‘r’ and ‘h’ be the radius and height of the sand cone respectively at time t.
Question 15:
The total cost C (x) associated with the production of ‘x’ units of an item is given by :
C (x) = 0.007 x3 – 0.003 x2 + 15x + 4000.
Find the marginal cost when 17 units are produced.
Answer:
Marginal cost is the rate of change of total cost with respect to output.
Now C (x) = 0·007 x3 – 0·003 x2 + 15x + 4000.
= (0·007) (3x2) – 0·003 (2x) + 15
When x = 17, MC = (0·007) (3(17)2) – 0·003 (2 (17)) + 15
= 6·069 – 0·102 + 15 = 20·967.
Hence, the reqd. marginal cost is ₹ 21 (nearly).
Question 16:
The total revenue received from the sale of ‘x’ units
of a product, is given by :
R (x) = 13x2 + 26x + 15.
Find the marginal revenue when x = 7.
Answer:
Marginal revenue is the rate of change of total
revenue with respect to number of units sold.
Now R(x) = 13x2 + 26x + 15.
= 26x + 26.
When x = 7, MR = 26 (7) + 26
= 182 + 26 = 208.
Hence, the reqd. marignal revenue is ₹ 208.
Question 17:
Choose the correct answer in
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is :
- 10
- 12
- 8
- 11
Answer:
12
Question 18:
The total revenue in Rupees received from the sale of ‘x’ units of a product is given by :
R (x) = 3x2 + 36x + 5.
The marginal revenue, when = 15, is :
- 116
- 96
- 90
- 126
Answer:
126
Question 19:
Show that the function given by f (x) = 3x + 17 is strictly increasing on R.
Answer:
Question 20:
Show that the function given by f (x) = e2x is strictly increasing on R.
Answer:
Question 21:
Show that the function given by f (x) = sin x is :
(c) neither increasing nor decreasing in (0, ).
Answer:
We have :
f (x) = sin x.
f′ (x) = cos x.
f′ (x) does not have same sign in (0, ).
Hence, ‘f’ is neither increasing nor decreasing in (0, ).
Question 22:
Find the intervals in which the function ‘f’ given by
f (x) = 2x2 – 3x is :
strictly increasing
Answer:
We have :
f (x) = 2x2 – 3x.
f′ (x) = 4x – 3.
(a) For f (x) to be strictly increasing function of x,
f′ (x) > 0
4x – 3> 0
Question 23:
Find the intervals in which the function ‘f’ given by
f (x) = 2x2 – 3x is :
strictly decreasing.
Answer:
Question 24:
Find the intervals in which the function ‘f’ given by :
f (x) = 2x3 – 3x2 – 36x + 7 is :
strictly increasing
Answer:
We have : f (x) = 2x3 – 3x2 – 36x + 7.
f′ (x) = 6x2 – 6x – 36.
For f (x) to be strictly increasing function of x :
f′ (x) > 0 i.e. 6x2 – 6x – 36 > 0
x2 – x – 6 > 0
(x – 3) (x + 2) > 0
(x – (– 2)) (x – 3) > 0
x (– , – 2) ∪ (3, ).
Hence, ‘f’ is strictly increasing in (– , – 2) ∪ (3, ).
Question 25:
Find the intervals in which the function ‘f’ given by :
f (x) = 2x3 – 3x2 – 36x + 7 is :
strictly decreasing.
Answer:
For f (x) to be strictly decreasing function of x,
f′ (x) < 0 i.e. 6x2 – 6x – 36 < 0
x2 – x – 6 < 0
(x – 3) (x + 2) < 0
(x – (– 2)) (x – 3) < 0
x (– 2, 3).
Hence, ‘f’ is strictly decreasing in (– 2, 3).
Question 26:
Find the intervals in which the following functions are strictly increasing or decreasing :
x2 + 2x – 5
Answer:
We have : f (x) = x2 + 2x – 5.
f′ (x) = 2x + 2.
(I) For f (x) to be strictly increasing function of x,
f ′ (x) > 0
i.e., if 2x + 2 > 0 i.e., if x > – 1.
Hence, f is strictly increasing in (–1, ).
(II) For f (x) to be strictly decreasing function of x,
f ′ (x) < 0
i.e.if 2x + 2 < 0 i.e., if x < – 1.
Hence, ‘f ’ is strictly decreasing in (– ,–1).
Question 27:
Find the intervals in which the following functions are strictly increasing or decreasing :
10 – 6x – 2x2
Answer:
We have : f (x) = 10 – 6x – 2x2.
f ′ (x) = – 6 – 4x.
(I) For f (x) to be strictly increasing function of x,
f ′ (x) > 0
i.e. if – 6 – 4x > 0 i.e. if 3 + 2x < 0
Question 28:
Find the intervals in which the following functions are strictly increasing or decreasing :
– 2x3 – 9x2 – 12x + 1
Answer:
We have :
f (x) = – 2x3 – 9x2 – 12x + 1.
f′ (x) = – 6x2 – 18x – 12.
(I) For f (x) to be strictly increasing function of x,
f ′ (x) > 0
i.e. if – 6x2 – 18x – 12 > 0
i.e. if x2 + 3x + 2 < 0
i.e. if (x + 2) (x + 1) < 0
i.e. (x – (– 2)) (x – (– 1) < 0
i.e. if – 2 < x < – 1.
Hence, ‘f’ is srictly increasing in (– 2, – 1).
(II) For f (x) to be strictly decreasing function of x,
f′ (x) < 0
i.e. if – 6x2 – 18x – 12 < 0
i.e. if x2 + 3x + 2 > 0
i.e. if (x + 2) (x + 1) > 0
i.e. if (x – (– 2)) (x – (– 1) > 0
i.e. if x < – 2 or x > – 1.
Hence, ‘f’ is strictly decreasing in (– , – 2) ∪ (– 1, ).
Question 29:
Find the intervals in which the following functions are strictly increasing or decreasing :
6 – 9x – x2
Answer:
We have : f (x) = 6 – 9x – x2.
f′ (x) = – 9 – 2x.
(I) For f (x) to be strictly increasing function of x,
f′ (x) > 0
i.e. if – 9 – 2x > 0 i.e. if 2x < – 9
Question 30:
Find the intervals in which the following functions are strictly increasing or decreasing :
(x + 1)3 (x – 3)3.
Answer:
We have : f (x) = (x + 1)3 (x – 3)3.
f′ (x) = (x + 1)3 . 3(x – 3)2 + 3 (x + 1)2 (x – 3)3
= 3 (x + 1)2 (x – 3)2 [(x + 1) + (x – 3)]
= 3 (x + 1)2 (x – 3)2 (2x – 2)
= 6 (x + 1)2 (x – 3)2 (x – 1).
(I) For f (x) to be strictly increasing function of x,
f ′ (x) > 0
i.e.if 6 (x + 1)2 (x – 3)2 (x – 1) > 0
i.e.if x – 1 > 0 [ 6 (x + 1)2 (x – 3)2 > 0]
i.e.if x > 1.
But f′ (x) = 0 at x = 3.
Hence, ‘f ’ is strictly increasing in (1, 3) ∪ (3, ).
(II) For f (x) to be strictly decreasing function of x,
f ′ (x) > 0
i.e.if 6 (x + 1)2 (x – 3)2 (x – 1) > 0
i.e.if x – 1 < 0 [ 6 (x + 1)2 (x – 3)2 > 0]
i.e. if x < 1.
But f′ (x) = 0 at x = – 1.
Hence, ‘f’ is strictly decreasing in (– , – 1) ∪ (– 1, 1).
Question 31:
Answer:
Question 32:
Find the values of ‘x’ for which y = [x (x – 2)]2 is an increasing function.
Answer:
We have :
y = [x (x – 2)]2 = x2 (x2 – 4x + 4)
= x4 – 4x3 + 4x2.
Question 33:
Answer:
Question 34:
Prove that the logarithmic function is strictly increasing on (0, ).
Answer:
Let f (x) = log x for x > 0.
Hence, ‘f’ is strictly increasing on (0, −).
Question 35:
f (x) = x2 – x + 1 is neither increasing nor decreasing strictly on (– 1, 1).
Answer:
We have : f (x) = x2 – x + 1.
Hence, f (x) is neither increasing nor decreasing on (– 1, 1).
Question 36:
cos x
Answer:
We have : f (x) = cos x.
Question 37:
cos 2x
Answer:
We have: f (x) = cos 2x.
f′ (x) = – 2 sin 2x.
Question 38:
cos 3x
Answer:
We have :
f (x) = cos 3x.
f′ (x) = – 3 cos 3x.
Question 39:
tan x
Answer:
We have : f (x) = tan x.
Question 40:
On which of the following intervals is the function f (x) = x100 + sin x – 1 strictly decreasing ?
(– 1, 1)
Answer:
For – 1 < x < 1
– 1 < x99 < 1
– 100 < 100 x99 < 100.
Also 0 < cos x < 1
f′ (x) is either + ve or – ve as (– 1, 1).
f (x) is neither increasing nor decreasing on (– 1, 1).
Question 41:
On which of the following intervals is the function f (x) = x100 + sin x – 1 strictly decreasing ?
(0, 1)
Answer:
For 0 < x < 1, x99 and cos x are both + ve
f′ (x) > 0
f (x) is increasing on (0, 1).
Question 42:
On which of the following intervals is the function f (x) = x100 + sin x – 1 strictly decreasing ?
Answer:
Question 43:
On which of the following intervals is the function f (x) = x100 + sin x – 1 strictly decreasing ?
Answer:
Question 44:
Find the least value of ‘a’ such that :
f (x) = x2 + ax + 1 is strictly increasing on (1, 2).
Answer:
We have :
f (x) = x2 + ax + 1.
f′ (x) = 2x + a.
Now 1 < x < 2
2 < 2x < 4
2 + a < 2x + a < 4 + a
2 + a < f′ (x) < 4 + a.
For f (x) to be increasing, f′ (x) 0
2 + a 0
a – 2.
Hence, the least value of a is – 2.
Question 45:
Answer:
Question 46:
Answer:
We have : f (x) = log sin x.
Question 47:
Answer:
Question 48:
Prove that the function given by
f (x) = x3 – 3x2 + 3x – 100 is increasing in R.
Answer:
We have :
f (x) = x3 – 3x2 + 3x – 100.
f′ (x) = 3x2 – 6x + 3 = 3 (x – 1)2,
which is 0 for all x R.
Hence, f (x) is increasing function on R.
Question 49:
The interval in which y = x2 e–x is increasing is :
- (– , )
- (– 2, 0)
- (2, )
- (0, 2)
Answer:
(0, 2)
Question 50:
Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
Answer:
The given curve is y = 3x4 – 4x.
Question 51:
Answer:
Question 52:
Find the slope of the tangent to the curve y = x3 – x + 1 at the point, where x – coordinate is 2.
Answer:
We have : y = x3 – x + 1.
Hence, the reqd. slope of the tangent = 11.
Question 53:
Find the slope of the tangent to the curve y = x3 – 3x + 2 at the point, where x-coordinate is 3.
Answer:
The given curve is y = x3 – 3x + 2
Question 54:
Find the slope of the normal to the curve :
Answer:
The given curve is :
x = a cos3 , y = a sin3 .
Question 55:
Find the slope of the normal to the curve :
Answer:
We have :
x = 1 – a sin and y = b cos2 .
Question 56:
Find points at which the tangent to the curve : y = x3 – 3x2 – 9x + 7 is parallel to the x-axis.
Answer:
The given curve is :
y = x3 – 3x2 – 9x + 7 ...(1)
(x – 3) (x + 1) = 0
x = – 1, 3.
When x = – 1, then from (1),
y = – 1 – 3 + 9 + 7 = 12.
When x = 3, then from (1),
y = 27 – 27 – 27 + 7 = – 20.
Hence, the reqd. points are (– 1, 12) and (3, – 20).
Question 57:
Find the point on the curve y = (x – 2)2, at which the tangent is parallel to the chord joining (2, 0) and (4, 4).
Answer:
The given curve is :
y = f(x) = (x – 2)2 ...(1)
f′ (x) = 2 (x – 2).
2x – 4 = 2
2x = 6
x = 3.
When x = 3, then from (1), y = (3 – 2)2 = 1.
Hence, the reqd. point is (3, 1).
Question 58:
Find the point on the curve y = x3 – 11x + 5 at which tangent is y = x – 11.
Answer:
The given curve is :
y = x3 – 11x + 5 ...(1)
The given line is y = x – 11 ...(2)
Slope of the line = 1.
Thus 3x2 – 11 = 1 3x2 = 12
x2 = 4 x = ± 2.
When x = 2, then from (1),
y = 8 – 22 + 5 = – 9.
When x = – 2, then from (1),
y = – 8 + 22 + 5 = 19.
Equation of tangent at (2, – 9) is :
y + 9 = 1. (x – 2)
y = x – 11.
Hence, (2, – 9) is the reqd. point.
Question 59:
Answer:
The given curve is :
The equation of reqd. lines are :
y + 1 = (– 1) (x – 0)
y + 1 = – x
y + x + 1 = 0
and y – 1 = (– 1) (x – 2)
y – 1 = – x + 2 y + x – 3 = 0.
Question 60:
Answer:
The given curve is :
Question 61:
Answer:
The given curve is :
Question 62:
Answer:
The given curve is :
Question 63:
Find the equations of the tangents and normals to the given curve at the indicated points :
y = x4 – 6x3 + 13x2 – 10x + 5 at (0, 5)
Answer:
The given curve is :
y = x4 – 6x3 + 13x2 – 10x + 5.
Question 64:
Find the equations of the tangents and normals to the given curve at the indicated points :
y = x4 – 6x3 + 13x2 – 10x + 5 at (1, 3)
Answer:
Question 65:
Find the equations of the tangents and normals to the given curve at the indicated points :
y = x3 at (1, 1)
Answer:
Question 66:
Find the equations of the tangents and normals to the given curve at the indicated points :
y = x3 at (0, 0)
Answer:
Question 67:
Find the equations of the tangents and normals to the given curve at the indicated points :
Answer:
Question 68:
Find the equation of the tangent line to the curve y = x2 – 2x + 7, which is :
parallel to the line 2x – y + 9 = 0
Answer:
The given curve is :
y = x2 – 2x + 7 ...(1)
Slope of the tangent = 2 (x – 1).
Slope of the line 2x – y + 9 = 0 is 2.
Since the tangent is parallel to the given line,
2 (x – 1) = 2 [ m1 = m2 ]
2x = 4 x = 2.
Putting in (1),y = 4 – 4 + 7 = 7.
The equation of the tangent at (2, 7) parallel to
2x – y + 9 = 0 is :
y – 7 = 2 (x – 2) 2x – y + 3 = 0
y – 2x – 3 = 0.
Question 69:
Find the equation of the tangent line to the curve y = x2 – 2x + 7, which is :
perpendicular to the line 5y – 15x = 13.
Answer:
Slope of the tangent = 2 (x – 1).
Slope of the line 5y – 15x = 13 is 3.
Since the tangent is perp. to the given line,
(2(x – 1)) (3)= – 1 [m1 m2 =−1]
Question 70:
Show that the tangents to the curve y = 7x3 + 11 at the points x = 2 and x = – 2 are parallel.
Answer:
The given curve is y = 7x3 + 11.
Hence, the tangents at the points where x = 2 and x = – 2 are parallel.
Question 71:
Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-co-ordiante of the point.
Answer:
Let P (x1, y1) be any point on the curve y = x3 ...(1)
x1 = 0 or 3.
When x1 = 0, then y1 = (0)3 = 0.
When x1 = 3, then y1 = 33 = 27.
Hence, the reqd. points are (0, 0) and (3, 27).
Question 72:
For the curve y = 4x3 – 2x5, find all the points at which the tangent passes through the origin.
Answer:
Let (x1, y1) be the reqd. point on the given curve :
y = 4x3 – 2x5 ...(1)
x1 = 0, x1 = ± 1.
When x1 = 0, then from (2),
y1 = 0.
When x1 = 1, then from (2),
y1 = (1) – 2 (1) = 2.
When x1 = – 1, then from (2),
y1 = 4 (– 1)3 – 2 (– 1)5
= – 4 + 2 = – 2.
Hence, the reqd. points are (0, 0), (1, 2) and (– 1, – 2).
Question 73:
Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to x-axis.
Answer:
The given curve is x2 + y2 – 2x – 3 = 0 ...(1)
1 – x = 0 x = 1.
Putting in (1), 1 + y2 – 2 (1) – 3 = 0
y2 = 4 y = ± 2.
Hence, the reqd. points are (1, ± 2).
Question 74:
Find the equation of the normal to the curve ay2 = x3 at (am2, am3).
Answer:
The given curve is ay2 = x3
Question 75:
Find the equations of the normals to the curve y = x3+ 2x + 6, which are parallel to the line x + 14y + 4 = 0.
Answer:
The given curve is :
y = x3 + 2x + 6 ...(1)
When x = 2, then from (1),
y = 8 + 4 + 6 = 18.
When x = – 2, then from (1),
y = – 8 – 4 + 6 = – 6.
Thus the co-ordinates of the points are (2, 18) and
(– 2, – 6).
The equations of the normals are :
14y – 252 = – x + 2 and 14y + 8y = – x – 2
x + 14y – 254 = 0 and x + 14y + 86 = 0.
Question 76:
Find the equations of the tangent and normal to the parabola y2 = 4ax at (at2, 2at).
Answer:
The given parabola is y2 = 4ax.
Question 77:
Prove that the curves x = y2 and xy = k cut at right angles if 8k2 = 1.
Answer:
The given curves are :
x = y2 ...(1)
and xy = k ...(2)
From (2), using (1), we get :
y2y = k y3 = k y = k1/3.
Putting in (1), x = k2/3.
Thus the given curves intersect at P (k2/3, k1/3).
Diff. (1) w.r.t. x,
Since the given curves cut at right angles at P,
m1m2 = – 1
Question 78:
Answer:
Question 79:
Answer:
The given curve is :
Question 80:
The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is :
- 3
- -3
Answer:
Question 81:
The line y = x + 1 is a tangent to the curve y2 = 4x at the point :
- (1, 2)
- (2, 1)
- (1, – 2)
- (– 1, 2)
Answer:
(1, 2)
Question 82:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
Answer:
Let y = x1/2, x = 25 and dx = 0·3.
Question 83:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
Answer:
Let y = x1/2, x = 49 and dx = 0·5.
Question 84:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
Answer:
Let y = x1/2, x = 0·64 and dx = – 0·04.
Question 85:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(0·009)1/3
Answer:
Let y = x1/3, x = 0·008
and dx = 0·001 so that x + dx = 0·009.
We require (x + dx)1/3.
Now y = (x + x)1/3 – x1/3
= (0·008 + 0·001)1/3 – (0·008)1/3
= (0·009)1/3 – 0·2
(0·009)1/3 = 0·2 + y.
Now y is approximately equal to :
Question 86:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(0·999)1/10
Answer:
Question 87:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(15)1/4
Answer:
Let y = x1/4 , x = 16,
dx = – 1 so that x + dx = 15.
We require (x + dx)1/4.
Now y = (x + )1/4 – x 1/4
= (16 − 1)1/4 – (16)1/4
= (15 )−1/4 – 2
(15)1/4 = 2 + y.
Now y is approximately equal to :
Question 88:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(26)1/3
Answer:
y = x1/3, x = 27
and dx = – 1 so that x + dx = 26.
We require (x + dx)1/3.
Now y = (x + y)1/3 – x1/3
= (27 – 1)1/3 – 3 = (26)1/3 – 3
(26)1/3 = 3 + y.
Now y is approximately equal to :
Question 89:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(255)1/4
Answer:
y = x1/4, x = 256, dx = – 1 so that x + dx = 255.
We require (x + dx)1/4.
Now y = (x +x)1/4 – x1/4
= (256 − 1)1/4 – 4 = (255)1/4 −4
(255)1/4 = 4 + y.
Now y, approximately equal to dy and
Question 90:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(82)1/4
Answer:
y = x1/4, x = 81, dx = 1
Question 91:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(401)1/2
Answer:
y = x1/2, x = 400 and dx = 1.
Question 92:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(0·0037)1/2
Answer:
Question 93:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(26·57)1/3
Answer:
Question 94:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(81·5)1/4
Answer:
Let y = x1/4, x = 81, dx = ·5
so that x + dx = 81·5.
We require (x + dx)1/4
Now y = (x + x)1/4 − x1/4
Question 95:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(3.968)3/2
Answer:
Question 96:
Using differentials, find the approximate value of each of the following up to 3 places of decimal :
(32.15)1/5
Answer:
Question 97:
Find the approximate value of f (2·01), where :
f (x) = 4x2 + 5x + 2.
Answer:
Let x = 2 and x = 0·01 ...(1)
Then f (2·01) = f (x + x)
= 4 (x + x)2 + 5 (x + x) + 2.
Now y = f (x + x) – f (x)
f (x + x) = f (x) + y
= f (x) + f′ (x) x [ dx = x]
f (2·01) = (4x2 + 5x + 2) + (8x + 5) x
= (4 (2)2 + 5 (2) + 2) + (8 (2) + 5) (0·01)
[Using (1)]
= (16 + 10 + 2) + (16 + 5) (0·01)
= 28 + 0·21 = 28·21.
Hence, approximate value of f (2·01) = 28·21.
Question 98:
Find the approximate value of f (5·001), where :
f (x) = x3 – 7x2 + 15.
Answer:
We have : f (x) = x3 – 7x2 + 15.
f′ (x) = 3x2 – 14x.
Now f (x + x) = f(x) + x f′ (x)
= (x3 – 7x2 + 15) + x (3x2 – 14x).
Taking x = 5 and x = 0·001, we get :
f (5·001) = (5)3 – 7 (5)2 + 15) + (0·001) (3 (5)2 – 14 (5))
= (125 – 175 + 15) + (0·001) (75 –70)
= – 35 + (0·001) (5)
= – 35 + 0·005 = – 34·995.
Question 100:
Find the approximate change in the volume ‘V’ of a cube of side ‘X’ metres caused by increasing the side by 1%.
Answer:
V, the volume of the cube = x3.
= (3x2) x
= (3x2) [0·01x] [ 1% 0f x = 0⋅01x]
= 0·03 x3 m3.
Hence, the approximate change in the volume
= 0·03 x3 m3.
Question 101:
Find the approximate change in the surface area of a cube of side ‘x’ metres caused by decreasing the side by 1%.
Answer:
Question 102:
If the radius of a sphere is measured as 7 m with an error 0·02 m, find the approximate error in calculating the volume.
Answer:
Question 103:
If the radius of a sphere is measured as 9 m with error of 0·03 cm, then find the approximate error in calculating its surface area.
Answer:
Let ‘r’ be the radius of the sphere and r be the error in measuring the radius.
Then r = 9 m and r = 0·03 m.
Now S, the surface area of the sphere is given by :
S = 4r2
= (8 (9)) (0·03) = 2·16 m2.
Hence, the approximate error in calculating the surface area is 2·16 m2.
Question 104:
If f (x) = 3x2 + 15x + 5, then the approximate value of f (3·02) is :
- 47·66
- 57·66
- 67·66
- 77·66
Answer:
77·66
Question 105:
The approximate change in the volume of a cube of side ‘x’ metres caused by increasing the side by 3% is :
- 0·06 x3 m3
- 0·6 x3 m3
- 0·09 x3 m3
- 0·9 x3m3.
Answer:
0·09 x3 m3
Question 106:
Find the maximum and minimum values, if any, of the following functions given by :
f (x) = (2x – 1)2 + 3
Answer:
We have : f (x) = (2x – 1)2 + 3.
Since (2x – 1)2 0,
Min. Value of (2x – 1)2 = 0.
Min. Value of f (x) = 3.
Max. value of f (x) does not exist.
Question 107:
Find the maximum and minimum values, if any, of the following functions given by :
f (x) = 9x2 + 12x + 2
Answer:
We have : f (x) = 9x2 + 12x + 2
= (3x + 2)2 – 2.
Min. value of (3x + 2)2 = 0
Min. value of f (x) = – 2.
Max. value of f (x) does not exist.
Question 108:
Find the maximum and minimum values, if any, of the following functions given by :
f (x) = – (x – 1)2 + 10
Answer:
We have : f (x) = – (x – 1)2 + 10.
Max. value of – (x – 1)2 = 0.
Max. value of f (x) = 10.
Min. value of f (x) does not exist.
Question 109:
Find the maximum and minimum values, if any, of the following functions given by :
f (x) = x3 + 1.
Answer:
Question 110:
f (x) = | x + 2 | – 1
Answer:
Question 111:
g (x) = – | x + 1 | + 3
Answer:
Question 112:
h (x) = sin 2x + 5
Answer:
We have : f (x) = sin 2x + 5.
Max. value of sin 2x =1
Max. value of sin 2x + 5 =1 + 5 = 6.
Min. value of sin 2x =– 1
Min. value of sin 2x + 5 = – 1 + 5 = 4.
Question 113:
f (x) =| sin 4x + 3 |
Answer:
We have : f (x) = | sin 4x + 3 |.
Max. value of sin 4x= 1
Max. value of | sin 4x + 3 | = | 1 + 3 | = | 4 | = 4.
Min. value of sin 4x= – 1
Min. value of | sin 4x + 3 | = | – 1 + 3 | = | 2 | = 2.
Question 114:
h (x) = x + 1, x (– 1, 1).
Answer:
We have :h (x) = x + 1.
As x , h (x) .
As x – , h (x) – .
Thus there is no max. and min. value.
However, when x = 1, h (x) = 2
when x = – 1, h (x) = 0.
Hence, max. value is 2 and min. value is 0.
Question 115:
Find the local maxima and local minima, if any, of the following functions. Find also the local
maximum and the local minimum value, as the case may be :
f (x) = x2
Answer:
We have : f (x) = x2.
f′ (x) = 2x, f ″ (x) = 2.
Now f′ (x) = 0 2x = 0 x = 0.
And f″ (0) = 2 (+ ve)
Hence, local minimum value at x = 0,
local min. value = f(0) = 0.
Question 116:
Find the local maxima and local minima, if any, of the following functions. Find also the local
maximum and the local minimum value, as the case may be :
g (x) = x3 – 3x
Answer:
We have : g (x) = x3 – 3x.
g′ (x) = 3x2 – 3, g″ (x) = 6x.
Now g′ (x)= 0 3x2 – 3 = 0 x2 = 1
x = ± 1.
And g″ (1) = 6 (1) = 6 ( + ve) and
g″ (– 1) = 6 (– 1) = – 6 ( – ve)
Hence, local minimum value is, at x = 1, local min. value =
g (1) = 1 – 3 (1) = – 2.
Local maximum value is, at x = – 1, local max. value
= g (– 1) = (– 1)3 – 3 (– 1) = – 1 + 3 = 2.
Question 117:
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum value, as the case may be :
Answer:
We have h (x) = sin x + cos x.
h′ (x) = cos x – sin x and
h′′ (x) = – sin x – cos x.
Now h′(x) = 0 cos x – sin x = 0
sin x = cos x tan x = 1
Question 118:
Find the local maxima and local minima, if any, of the following functions. Find also the local
maximum and the local minimum value, as the case may be :
f (x) = sin x – cos x, 0 < x < 2
Answer:
We have : f (x) = sin x – cos x.
f′ (x) = cos x + sin x
and f″ (x) = – sin x + cos x.
Now f′ (x) = 0
cos x + sin x= 0 sin x = – cos x
Question 119:
Find the local maxima and local minima, if any, of the following functions. Find also the local
maximum and the local minimum value, as the case may be :
f (x) = x3 – 6x2 + 9x + 15
Answer:
We have : f(x) = x3 – 6x2 + 9x + 15.
f′ (x) = 3x2 – 12x + 9
and f ″ (x) = 6x – 12.
Now f ′ (x) = 0 3x2 – 12x + 9 = 0
x2 – 4x + 3 = 0
(x – 1) (x – 3) = 0 x = 1, 3.
And f ″ (1) = 6 (1) – 12 = – 6 (– ve),
f ″ (3) = 18 – 12 = 6 (+ ve)
Hence, local max. is at x = 1, local max. value
= 1 – 6 + 9 + 15 = 19.
Local min is at x = 3, local min. value
= 27 – 6 (9) + 9 (3) + 15
= 27 – 54 + 27 + 15 = 15.
Question 120:
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum value, as the case may be :
Answer:
Question 121:
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum value, as the case may be :
Answer:
Question 122:
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum value, as the case may be :
Answer:
Question 123:
Prove that the following functions do not have maxima or minima :
f (x) = ex
Answer:
We have : f (x) = ex.
f ′ (x) = ex.
Now f ′ (x) = 0
ex= 0,
which gives no real value of x.
Hence, f (x) does not have maximum or minimum values.
Question 124:
Prove that the following functions do not have maxima or minima :
f (x) = log x
Answer:
We have f (x) = log x.
which gives no real value of x.
Hence, f (x) does not have maximum or minimum values.
Question 125:
Prove that the following functions do not have maxima or minima :
f (x) = x3 + x2 + x + 1.
Answer:
We have : f (x) = x3 + x2 + x + 1.
f′ (x) = 3x2 + 2x + 1.
Now f′ (x) = 0
3x2 + 2x + 1 = 0
which are non-real.
Hence, f (x) does not have maximum and minimum values.
Question 126:
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals :
f (x) = x3, x [– 2, 2]
Answer:
We have : f (x) = x3, x [– 2, 2].
f′ (x) = 3x2.
For extreme values,
f′ (x) = 0 3x2 = 0
x = 0 [– 2, 2].
Now f (– 2) = (– 2)3 = – 8
f (0) = (0)3 = 0
and f (2) = 23 = 8.
Hence, absolute max. value is 8,which is attained at x = 2
and absolute min. value is – 8, which is attained at
x = – 2.
Question 127:
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals :
f (x) = sin x + cos x, x [0, ]
Answer:
We have : f (x) = sin x + cos x, x [0, ].
f′ (x) = cos x – sin x.
For extreme values,
f′ (x) = 0
cos x – sin x= 1
sin x = cos x
Question 128:
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals :
Answer:
We have :
Question 129:
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals :
f (x) = (x – 1)2 + 3, x [– 3, 1].
Answer:
We have :
f (x) = (x – 1)2 + 3, x [– 3, 1].
f′ (x) = 2 (x – 1).
For extreme values, f ′ (x) = 0
2 (x – 1) = 0
x – 1 = 0 x = 1 [– 3, 1].
Now f (– 3) = (– 4)2 + 3 = 16 + 3 = 19
and f (1) = (0)2 + 3 = 0 + 3 = 3.
Hence, absolute max. value is 19, which is attained at
x = – 3.
and absolute min. value is 3, which is attained at x = 1.
Question 130:
Find the maximum profit that a company can make,
if the profit function is given by :
p (x) = 41 – 24x – 18x2
Answer:
p (x) = 41 – 24x – 18x2.
p′ (x) = – 24 – 36x and p″ (x) = – 36.
Now p′ (x) = 0
– 24 – 36x = 0 3x = – 2
Question 131:
Find both maximum value and minimum value of 3x4 – 8x3 + 12x2 – 48x + 25 in the interval [0, 3].
Answer:
We have :
f (x) = 3x4 – 8x3 + 12x2 – 48x + 25.
f′ (x) = 12x3 – 24x2 + 24x – 48.
Now f′ (x) = 0
12x3 – 24x2 + 24x – 48 = 0
x3 – 2x2 + 2x – 4 = 0
x2 (x – 2) + 2 (x – 2) = 0
(x2 + 2) (x – 2) = 0
x = 2.
f (0) = 25
f (2) = 3 (16) – 8 (8) + 12 (4) – 48 (2) + 25
= 48 – 64 + 48 – 96 + 25
= 121 – 160 = – 39.
f (3) = 3 (81) – 8 (27) + 12 (9) – 48 (3) + 25
= 243 – 216 + 108 – 144 + 25
= 376 – 360 = 16.
Hence, max. value is 25 and min value is – 39.
Question 132:
At what point in the interval [0, 2] does the function sin 2x attain its maximum value ?
Answer:
We have :
f (x) = sin 2x, 0 ≤ x ≤ 2
so that f′ (x) = 2 cos 2x, 0 < x < 2.
Now f′ (x)= 0
2 cos 2x= 0, 0 < x < 2
cos 2x = 0, 0 < x < 2
Question 133:
What is the maximum value of the function sin x + cos x ?
Answer:
We have :
f (x) = sin x + cos x ; x [0, 2] (say)
f ′ (x) = cos x – sin x.
For extreme values, f ′ (x) = 0
cos x – sin x= 0
sin x = cos x tan x = 1
Question 134:
Find the maximum value of 2x3 – 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [– 3, – 1].
Answer:
We have :
f (x) = 2x3 – 24x + 107, x [1, 3].
f′ (x) = 6x2 – 24.
(i) For extreme values, f′ (x) = 0
6x2 – 24 = 0
x2 = 4 x = ± 2
x = 2 [1, 3].
Now f (1) = 2 (1) – 24 (1) + 107
= 2 – 24 + 107 = 85
f (2) = 2 (8) – 24 (2) + 107
= 16 – 48 + 107 = 75
and f (3) = 2 (27) – 24 (3) + 107
= 54 – 72 + 107 = 89.
Hence, max. value = 89, which is attained at x = 3.
(ii) We have :
f (x) = 2x3 – 24x + 107,x [– 3, – 1].
f′ (x) = 6x2 – 24.
For extreme values,
f ′ (x) = 0
6x2 – 24 = 0 x2 – 4 = 0 x2 = 4
x = ± 2 x = – 2 [– 3, – 1].
Now f (– 3) = 2 (– 27) – 24 (– 3) + 107
= – 54 + 72 + 107 = 125
f (– 2) = 2 (– 8) – 24 (– 2) + 107
= – 16 + 48 + 107 = 139
f (– 1) = 2 (– 1) – 24 (– 1) + 107
= – 2 + 24 + 107 = 129.
Hence, max. value = 139,
which is attained at x = – 2.
Question 135:
It is given that at x = 1, the function x4 – 62x2 + ax + 9 attains its maximum value in the interval [0, 2]. Find the value of ‘a’.
Answer:
We have : f (x) = x4 – 62x2 + ax + 9.
f′ (x) = 4x3 – 124x + a
and f″ (x) = 12x2 – 124.
Now f′ (1) = 0 [Given]
4 (1) – 124 (1) + a = 0
a = 120.
Now f ″(1) = 12 (1) – 124 = – 112 < 0.
Thus f (x) attains its maximum value at x = 1, where a = 120.
Hence, a = 120.
Question 136:
Find the maximum and minimum values of :
x + sin 2x on [0, 2].
Answer:
We have : f (x)= x + sin 2x.
f′ (x) = 1 + 2 cos 2x.
Now f′ (x) = 0
1 + 2 cos 2x = 0
Question 137:
Find two numbers whose sum is 24 and whose product is as large as possible.
Answer:
Let x and y be two numbers.
By the question, x + y = 24 ...(1)
Let the product, P = xy
P = x (24 – x)
P = 24 – x2.
Question 138:
Find the positive numbers x and y such that x + y = 60 and xy3 is maximum.
Answer:
We have :
x + y = 60 ...(1)
Let P = xy3
= x (60 – x)3 [Using (1)]
Question 139:
Find the positive numbers x and y such that their sum is 35 and the product x2y5 is maximum.
Answer:
We have : x + y = 35 ...(1)
Let P = x2y5
= x2 (35 – x)5.
Question 140:
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Answer:
Let ‘x’, and ‘y’ be the two positive numbers.
By the question, x + y = 16
y = 16 – x ...(1)
Let S = x3
+ y3 = x3 + (16 – x)3.
Question 141:
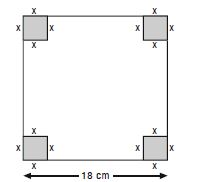
A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum ?
Answer:
Let ‘x’ cm, be the side of the square cut from each corner.
Length of the resulting box = 18 – 2x ;
Breadth of the resulting box = 18 – 2x ;
Height of the resulting box = x.
Volume = (18 – 2x)2. x
Let V (x) = x (18 – 2x)2.
V′ (x) = x.2 (18 – 2x) (– 2) + (18 – 2x)2 (1)
= (18 – 2x) [– 4x + 18 – 2x]
= (18 – 2x) (18 – 6x).
For max./min. volume, V′ (x) = 0
(18 – 2x) (18 – 6x) = 0
x = 9 or x = 3.
But x = 9 is impossible.
[ The whole of thin sheet will be cut off]
Thus x = 3.
Now V″ (x) = (18 – 2x) (– 6) + (18 – 6x) (– 2)
= – 108 + 12x – 36 + 12x
= 24x – 144.
V″ (x = 3) = 24 (3) – 144
= 72 – 144 = – 72,
which is – ve.
V (x) is max. when x = 3.
Hence, the length of the side of the square cut off from
each corner = 3 cm.
Question 142:
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?
Answer:
Let ‘x’ cm. be the side of the square cut off from each corner.
Length of the resulting box = 45 – 2x.
Breadth of the resulting box = 24 – 2x.
Height of the resulting box = x.
Volume, V = (45 – 2x) (24 – 2x) x
= 2x (45 – 2x) (12 – x).
V (x) = 2 (2x3 – 69x2 + 540x).
V′ (x) = 2 (6x2 – 138x + 540)
= 12 (x2 – 23x + 90).
For max. / min., V′= 0
12 (x2 – 23x + 90) = 0
(x – 5) (x – 18) = 0
x = 5, 18.
But x =18 is impossible.
x = 5.
Also V″ (x) = 12 (2x – 23).
V″ (5) = 12 (10 – 23)
= (12) (– 13) = – 156 < 0
Thus x = 5 for max. value.
Hence, length of the side of the square cut off for each
corner is 5 cm.
Question 143:
Show that of all rectangles inscribed in a given fixed circle the square has the maximum area.
Answer:
Let ‘x’ and ‘y’ be the length and breadth of the rectangle, which is inscribed in a fixed circle of radius ‘a’.
Then x2 + y2 = (2a)2
x2 + y2 = 4a2 ...(1)
Now A, the area of the rectangle = xy
Question 144:
Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.
Answer:
Let ‘S’ and ‘V’ be the surface area and volume
of the cylinder, whose radius is ‘r’ and height ‘h’.
Surface area, S = 2r2 + 2rh
Question 145:
Of all closed cylindrical cans (right circular) of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area.
Answer:
Let ‘r’ be the radius and ‘h’, the height of cylindrical can.
Volume = r2h = 100
Question 146:
A wire of length 28 cm is to be cut into two pieces. One of the pieces is to be made into a square and other into a circle. What could be the lengths of the two pieces so that the combined area of the square and the circle is minimum ?
Answer:
Let one piece be x m.
Other piece is (28 – x) m.
Let ‘x’ metres be made into a circle and (28 – x) metres be
made into a square.
2r = x
Question 147:
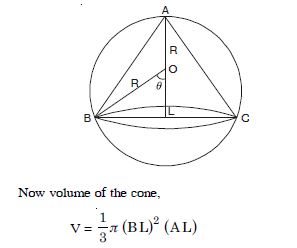
Answer:
Let the cone ABC be inscribed in a sphere of radius R.
Let ∠BOL = .
BL, radius of the base of the cone = R sin
and AL height of the cone = AO + OL
= R + R cos .
Question 148:
Answer:
Let ‘r’ and ‘h’ be the radius and height respectively of the cone ABC.
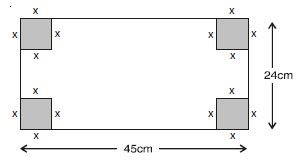
Question 149:
Answer:
Let ‘l’ be the given slant height and ‘’ be the
semi-vertical angle.
r, radius of the base = l sin
and h, height of the cone = l cos .
Question 150:
Answer:
Let ‘S’ be the given surface of the cone whose
radius is ‘r’, ‘h’ the height and ‘l’, the slant height.
S = r2 + rl ...(1)
Question 151:
Choose the correct answer in
The point on the curve x2 = 2y, which is nearest to the point (0, 5) is :
- (0, 0)
- (2, 2)
Answer:
Question 152:
- 0
- 1
- 3
Answer:
Question 153:
- 1
- 0
Answer:
1
Question 154:
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is :
- 10
- 12
- 8
- 11
Answer:
12
Question 155:
The total revenue received from the sale of x units of a product is given by R (x) = 3x2 + 36 + 5. The marginal revenue, when x = 15 is:
- 116
- 96
- 90
- 126
Answer:
126
Question 156:
The interval, in which y = x2e–x is increasing is :
- (–,)
- (– 2, 0)
- (2,)
- (0, 2)
Answer:
The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is :
- 2
- –3
Question 157:
The line y = x + 1 is a tangent to the curve y2 = 4x at the point :
- (1, 2)
- (2, 1)
- (1, –2)
- (–1, 2)
Answer:
(1, 2)
Question 158:
If f (x) = 3x2 + 15x + 5, then the approximate value of f (3.02) is :
- 47.66
- 57.66
- 67.66
- 77.66.
Answer:
77.66.
Question 159:
The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is:
- 0.06 x3 m3
- 0.6 x3 m3
- 0.09 x3 m3
- 0.9 x3 m3
Answer:
0.09 x3 m3
Question 160:
The point on the curve x2 = 2y, which is nearest to the point (0, 5), is :
- (0, 0)
- (2, 2)
Answer:
Question 161:
For all real values of x, the minimum value of
- 0
- 1
- 3
Answer:
Question 162:
The maximum value of [x(x – 1) + ]1/3, 0 ≤ x ≤ 1 is :
- 1
- 0
Answer:
1
Question 163:
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic m per metre. Then the depth of the wheat is increasing at the rate of :
- 1 m3/minute
- 0.1 m3/minute
- 1.1 m3/minute
- 0.5 m3/minute.
Answer:
1 m3/minute
Question 164:
The slope of the tangent to the curve x = t2 + 3t – 8, y = 2 t2 – 2t + 5 at the point (2, –1) is :
Answer:
Question 165:
The line y = mx + 1 is a tangent to the curve y2 = 4x if the value of m is :
- 1
- 2
- 3
Answer:
1
Question 166:
The normal at the point (1, 1) on the curve 2y + x2 = 3 is :
- x + y = 0
- x – y = 0
- x + y + 1 = 0
- x – y + 1 = 0
Answer:
x – y = 0
Question 167:
The normal to the curve x2 = 4y passing through (1, 2) is :
- x + y = 3
- x – y = 3
- x + y = 1
- x – y = 1
Answer:
x + y = 3
Question 168:
The point on the curve 9y2 = x3, where the normal to the curve makes equal intercepts with the axes are :