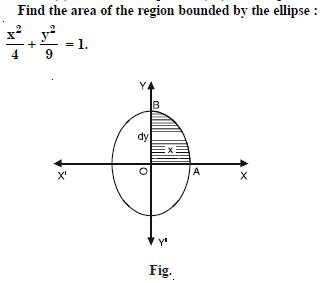
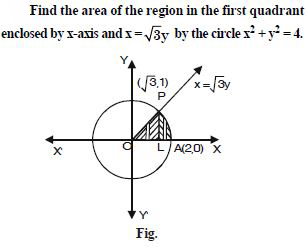
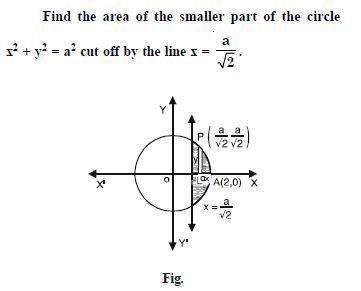
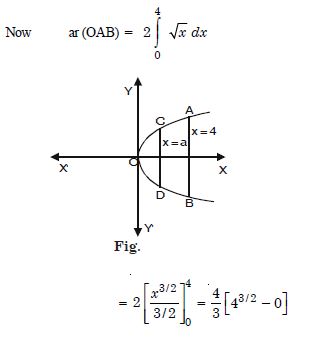
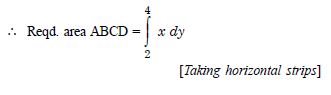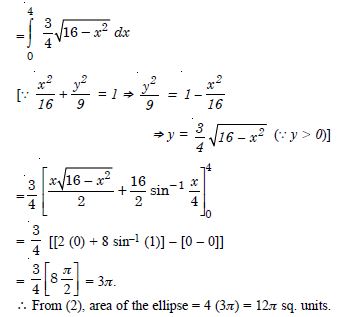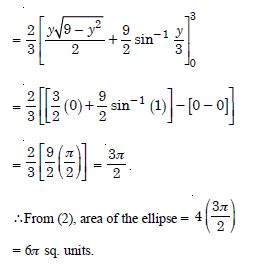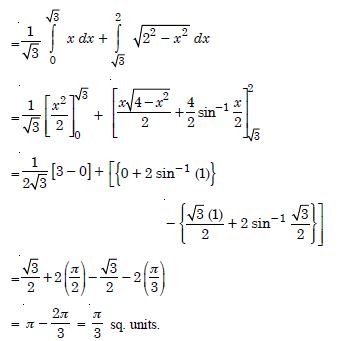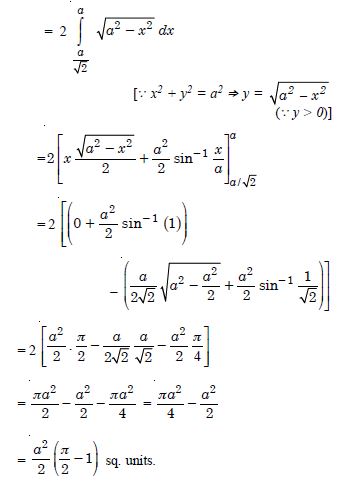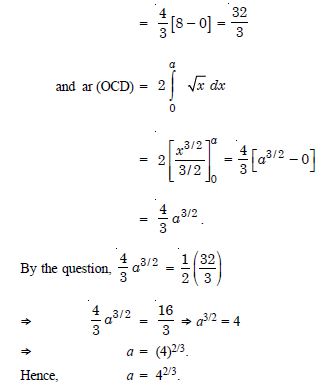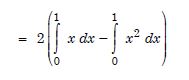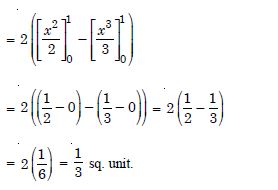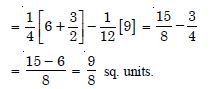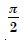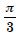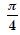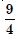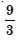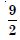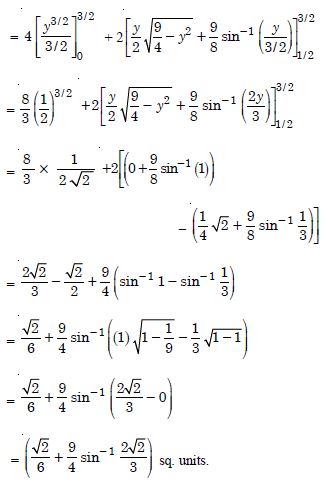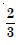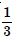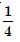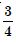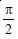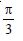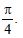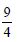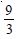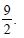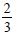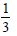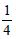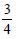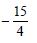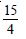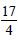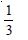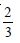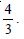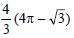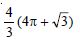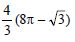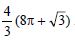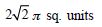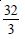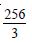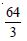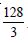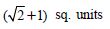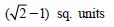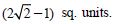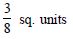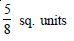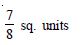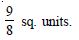Question 1:
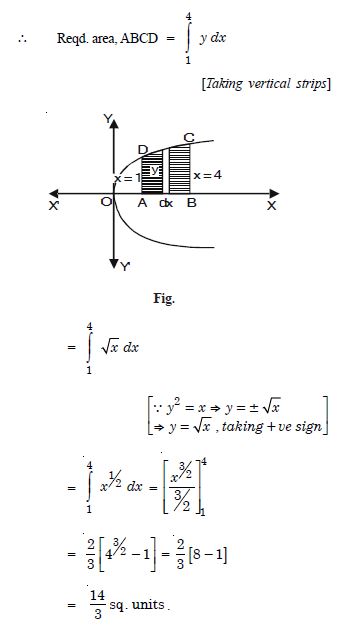
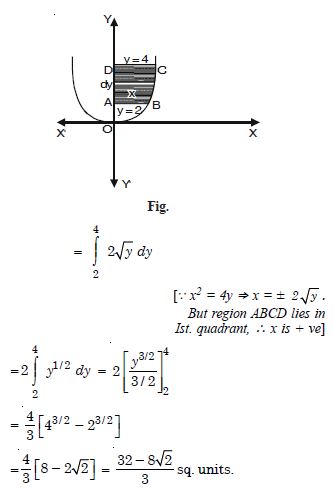
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Answer:
y2 = x is right-handed parabola.
Question 2:
Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Answer:
The given parabola is y2 = 9x ..(1)
Question 3:
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Answer:
x2 = 4y dx is an upward parabola.
Question 4:
Answer:
Question 5:
Answer:
Question 6:
Answer:
Question 7:
Answer:
Question 8:
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Answer:
We have : x = y2 ....(1)
and x = 4 ...(2)
Question 9:
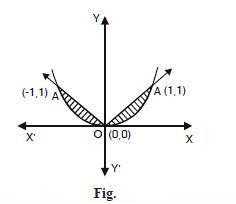
Find the area of the region bounded by the parabola y = x2 and y = | x |.
Answer:
The given parabola is x2 = y ...(1)
This is an upward parabola with vertex (0, 0).
y = | x | represents the st. lines :
y = x and y = –x ...(2)
y = x meets (1) at O (0, 0) and A (1, 1)
y = – x meets (1) at O (0, 0) and A¢ (– 1, 1).
\ Reqd. area = 2 (Shaded area in first quadrant)
Question 10:
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2.
Answer:
The given curve is x2 = 4y ...(1),
which is an upward parabola with vertex (0, 0).
The given line is x = 4y – 2 ...(2)
Solving (1) and (2) :
Question 11:
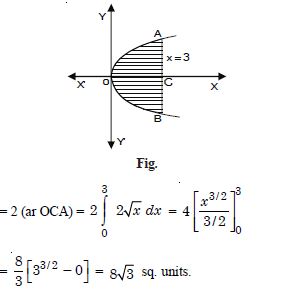
Find the area of the region bounded by the curve y2 = 4x and the line x = 3.
Answer:
The given curve is y2 = 4x ...(1)
and the given line is x = 3 ...(2)
Reqd. area = Shaded area
Question 12:
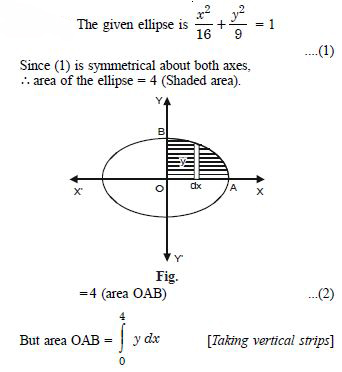
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is :
Answer:
Question 13:
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is :
- 2
Answer:
Question 14:
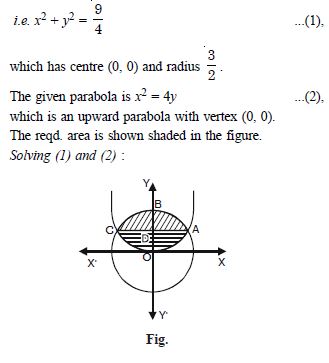
Find the area of the circle 4x2 + 4y2 = 9, which is interior to the parabola x2 = 4y.
Answer:
The given circle is 4x2 + 4y2 = 9
Question 15:
Find the area bounded by curves :
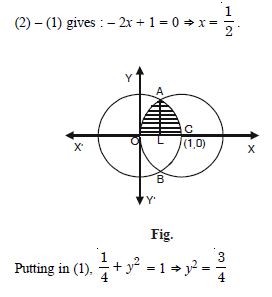
(x – 1)2 + y2 = 1 and x2 + y2 = 1.Answer:
The given circles are :
x2 + y2 = 1 ....(1)
and (x – 1)2 + y2 = 1 ....(2)
(1) is a circle with centre (0, 0) and radius 1.
(2) is a circle with centre (1, 0) and radius 1.
Solving (1) and (2) :
Question 16:
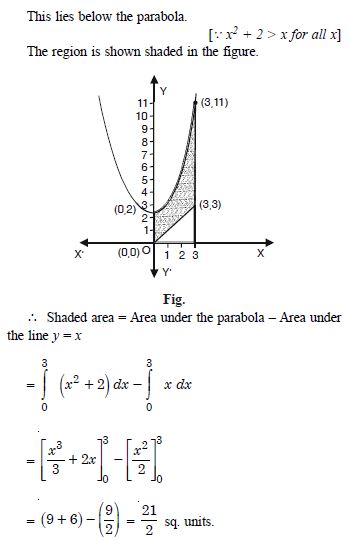
Find the area bounded by the curves :
y = x2 + 2, y = x, x = 0 and x = 3.
Answer:
y = x2 + 2 is a parabola.
For tracing, we have the table :
Question 17:
Using integration, find the area of the region bounded by the triangle whose vertices are :
(– 1, 0), (1, 3) and (3, 2).
Answer:
Let A (– 1, 0), B (1, 3) and C (3, 2) be the
vertices of the triangle as shown in the figure.
Question 18:
Using integration, find the area of the triangular region whose sides have the equations :
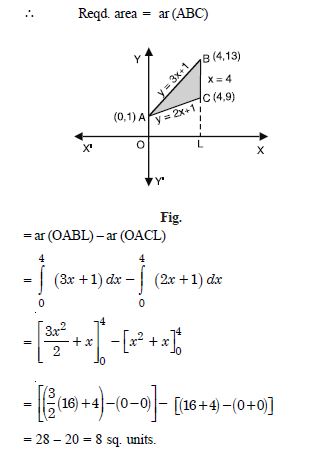
y = 2x + 1, y = 3x + 1 and x = 4.
Answer:
The given lines are :
y = 2x + 1 ...(1)
y = 3x + 1 ...(2)
and x = 4 ...(3)
Solving (1) and (2) : we get x = 0, y = 1.
Thus lines (1) and (2) intersect at A (0, 1).
Similarly lines (2) and (3) intersect at B (4, 13)
and lines (3) and (1) intersect at C (4, 9). [Do it]
Question 19:
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is :
- 2 ( – 2)
- – 2
- 2 – 1
- 2 ( + 2)
Answer:
– 2
Question 20:
Area lying between the curves y2 = 4x and y = 2x is :
Answer:
Question 21:
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is :
Answer:
Question 22:
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is :
- 2
Answer:
Question 23:
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is :
- 2 ( – 2)
- – 2
- 2 – 1
- 2 ( + 2)
Answer:
– 2
Question 24:
Area lying between the curves y2 = 4x and y = 2 is :
Answer:
Question 25:
Area bounded by the curve y = x3, the x-axis and the ordinates x = – 2 and x = 1 is :
- – 9
Answer:
Question 26:
The area bounded by the curve y = x | x |, x-axis and the ordinates x = – 1 and x = 1 is given by :
- 0
Answer:
Question 27:
The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is :
Answer:
Question 28:
The area enclosed by the circle x2 + y2 = 2 is equal to :
- 4 sq. units
- 42 sq. units
- 2 sq. units.
Answer:
2 sq. units.
Question 29:
The area enclosed by the circle x2 + y2 = 2 is equal to :
- 4 sq. units
- 42 sq. units
- 2 sq. units.
Answer:
2 sq. units.
Question 30:
- 2ab
- ab
- a2b
- ab2
Answer:
ab
Question 31:
The area of the region bounded by the curve y = x2 and the line y = 16 is :
Answer:
Question 32:
Answer:
Question 33:
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is :