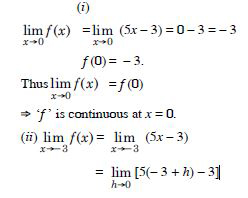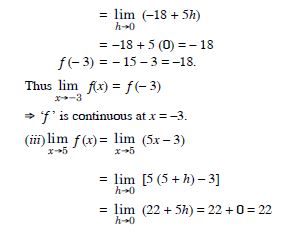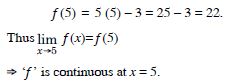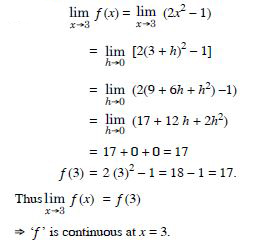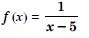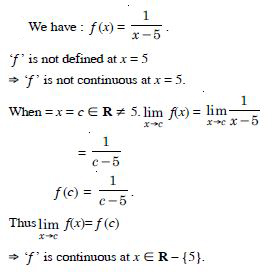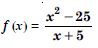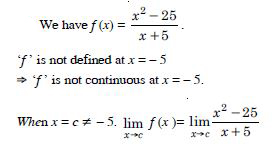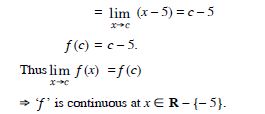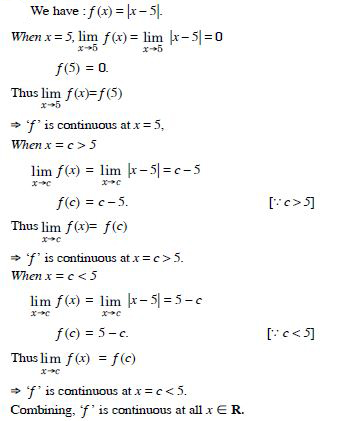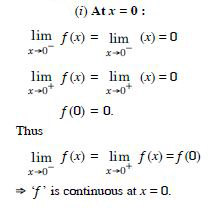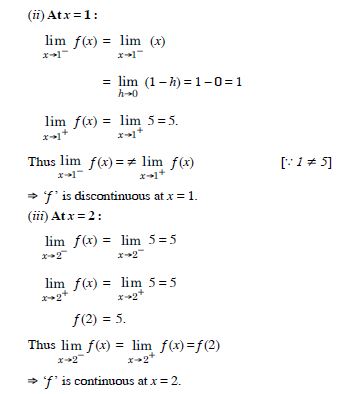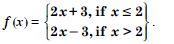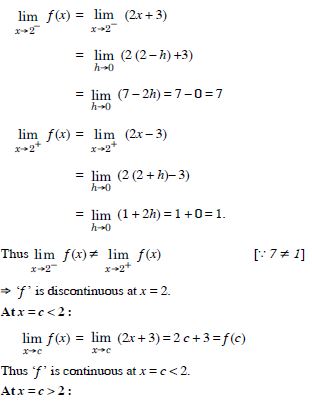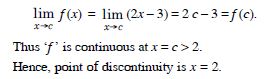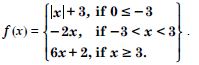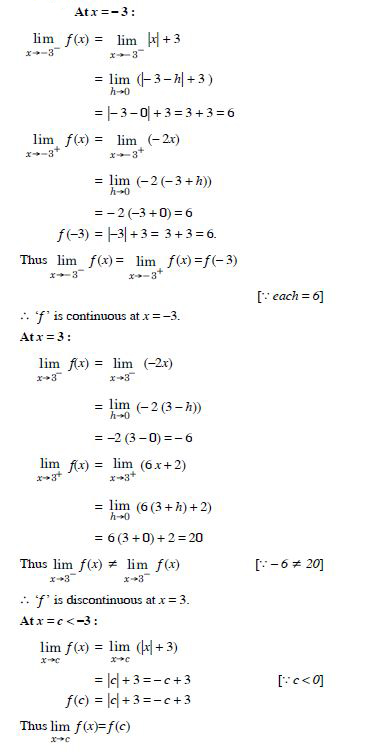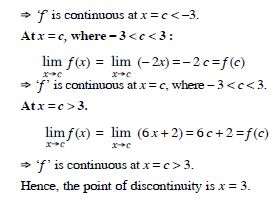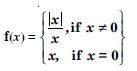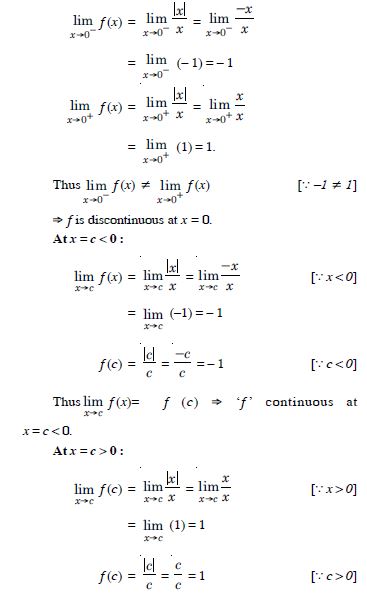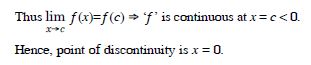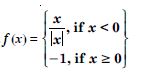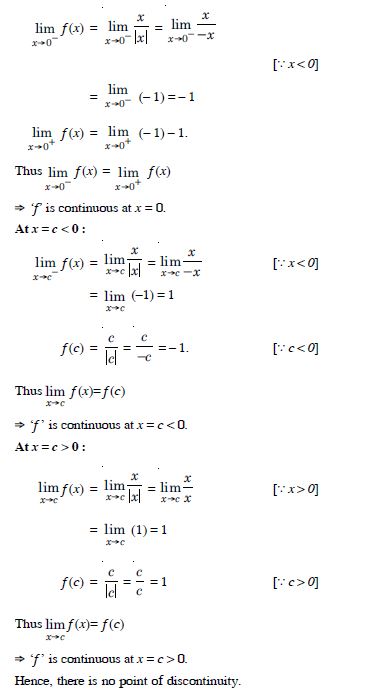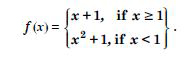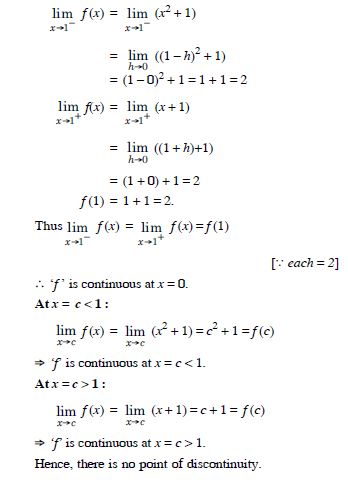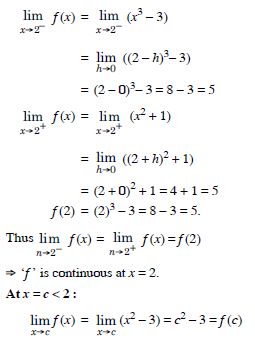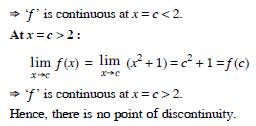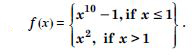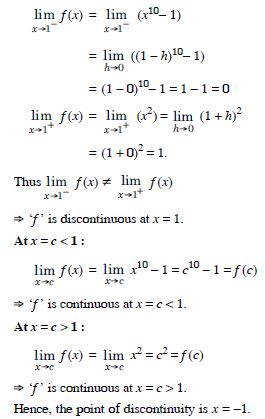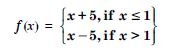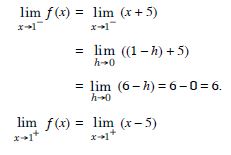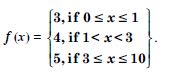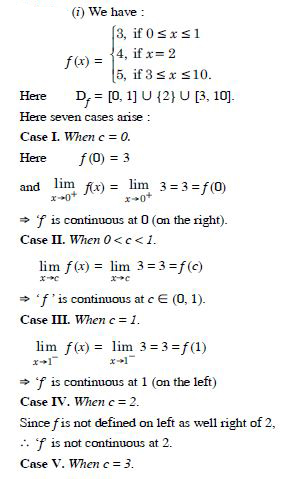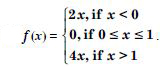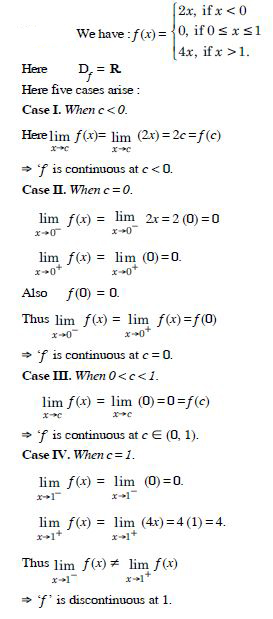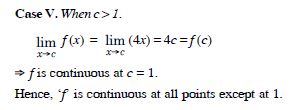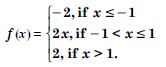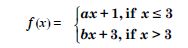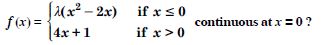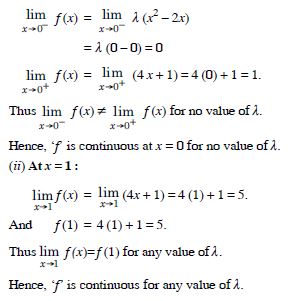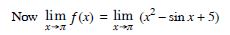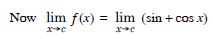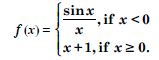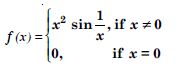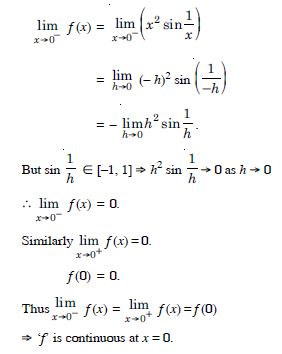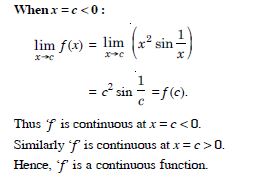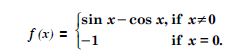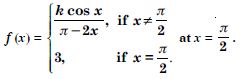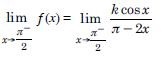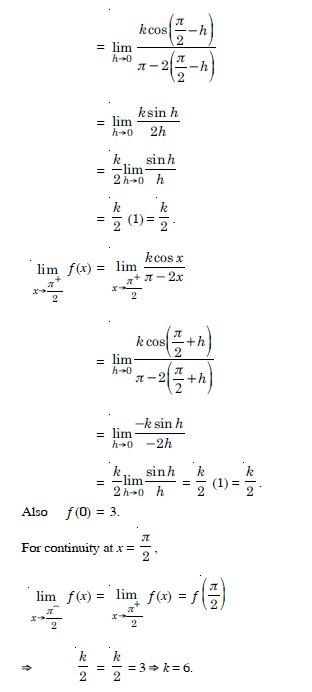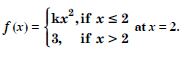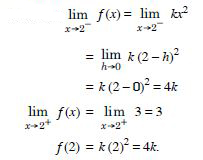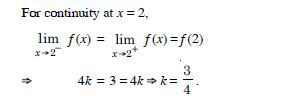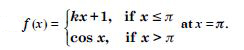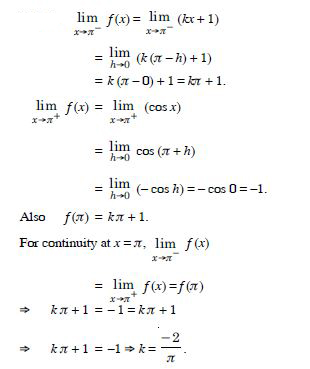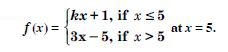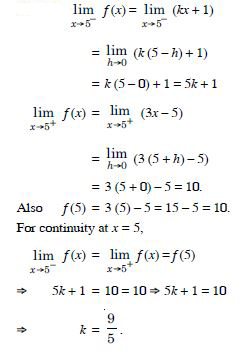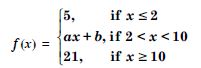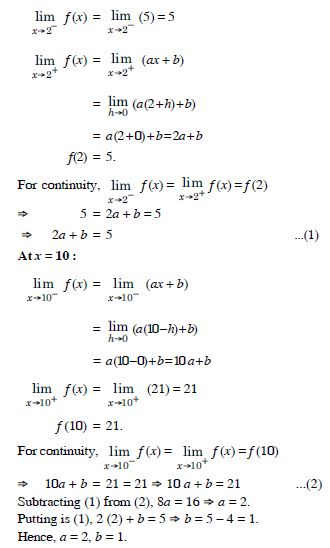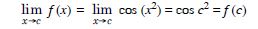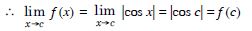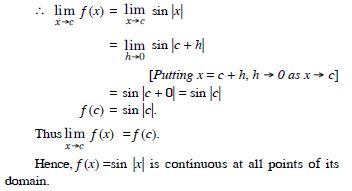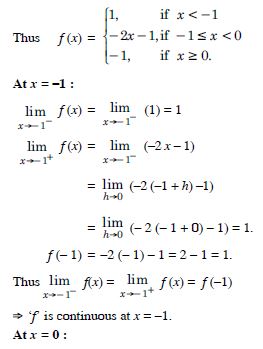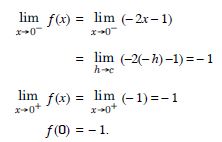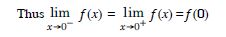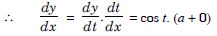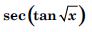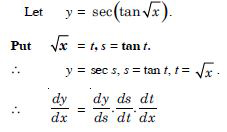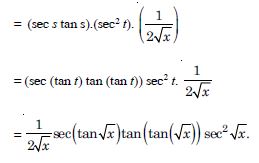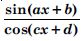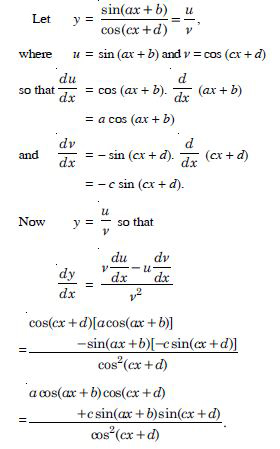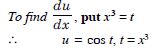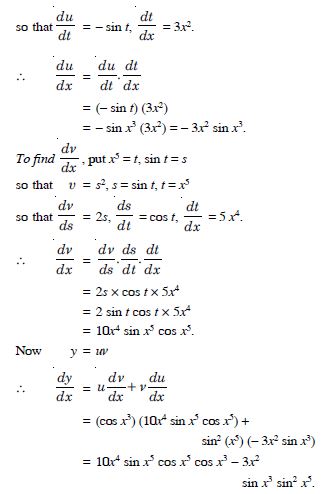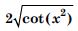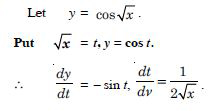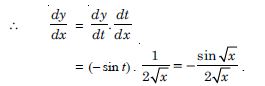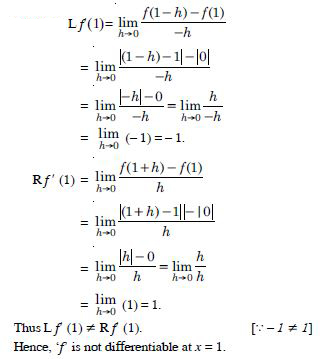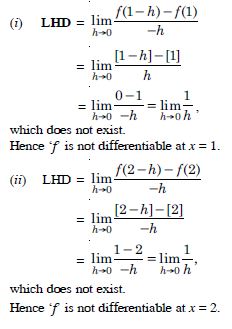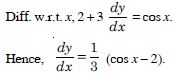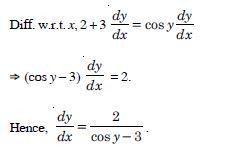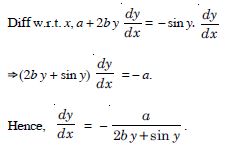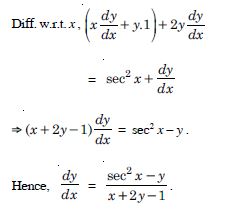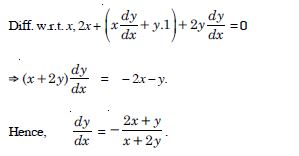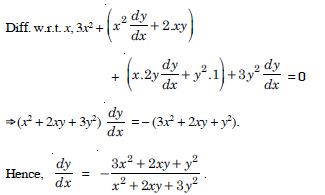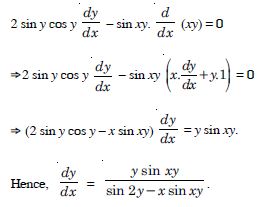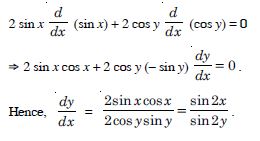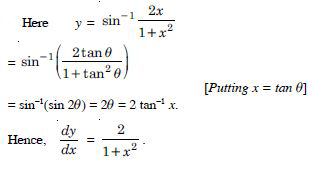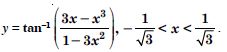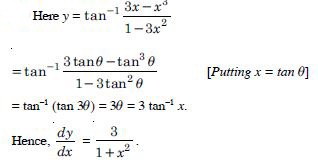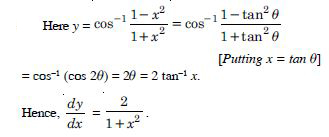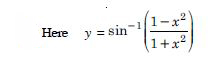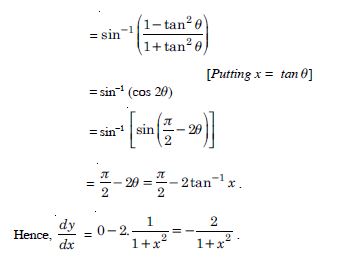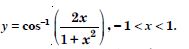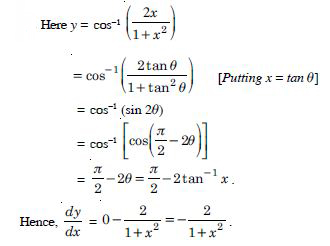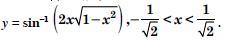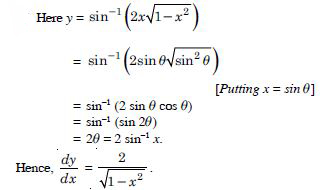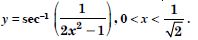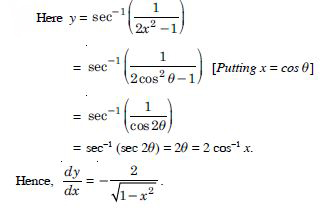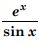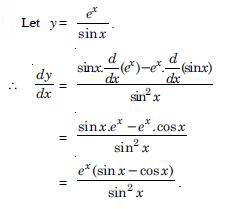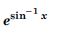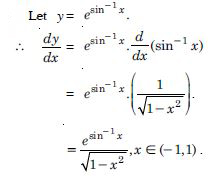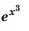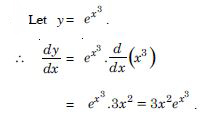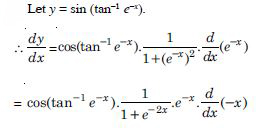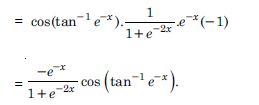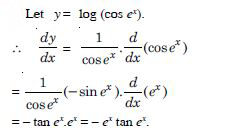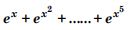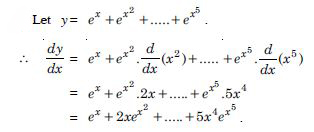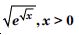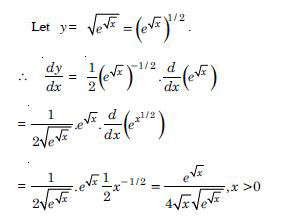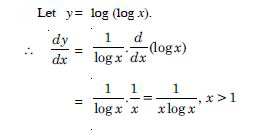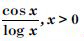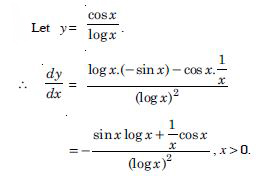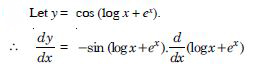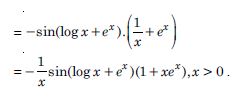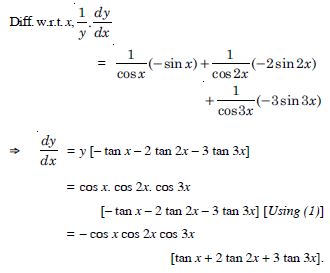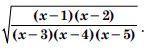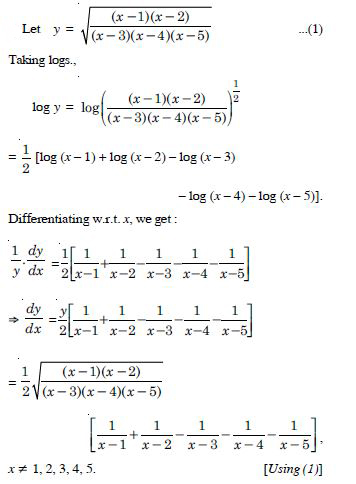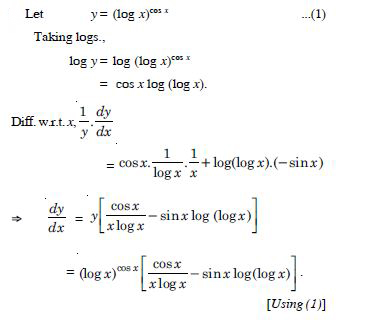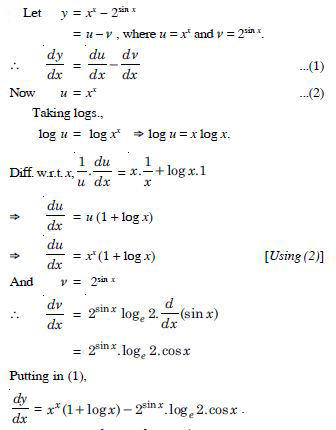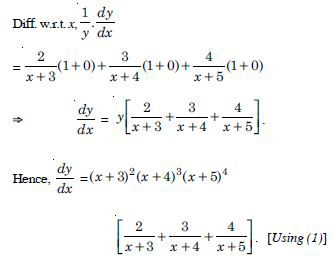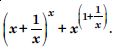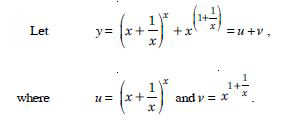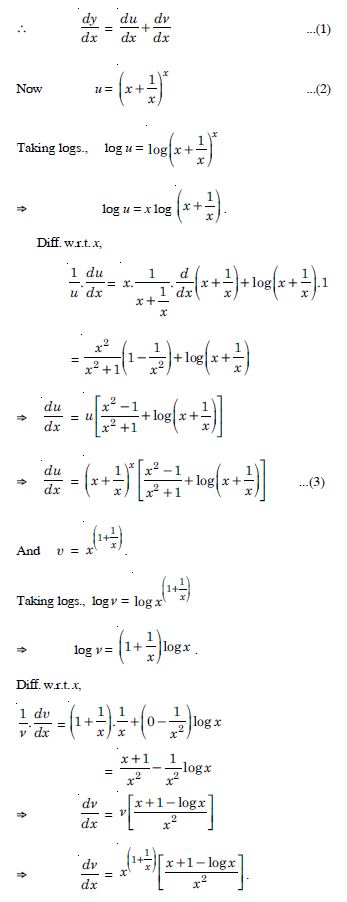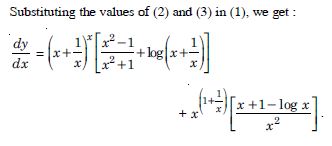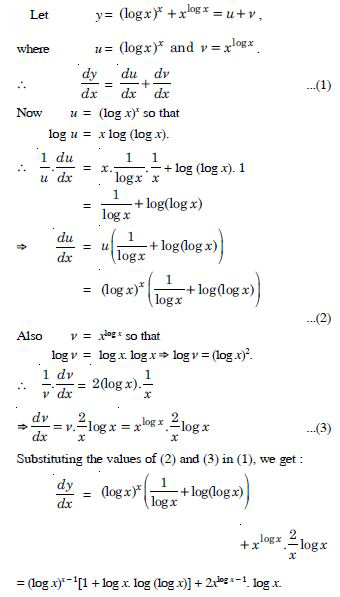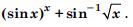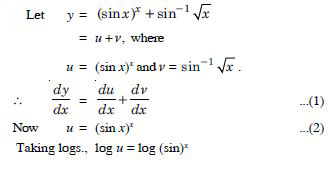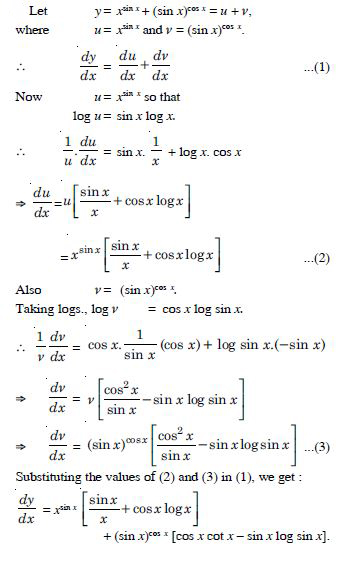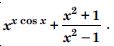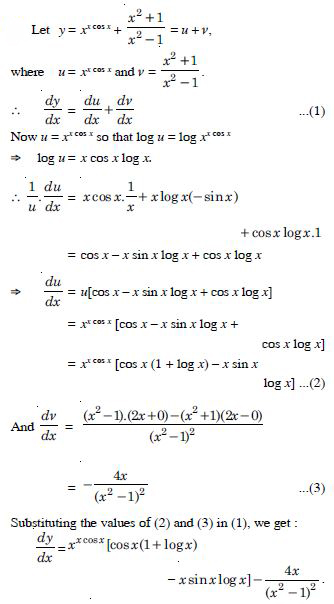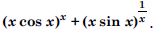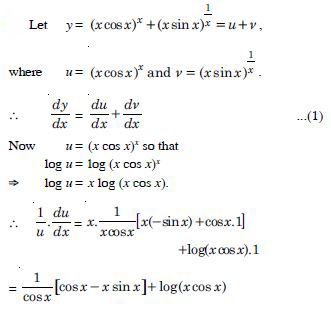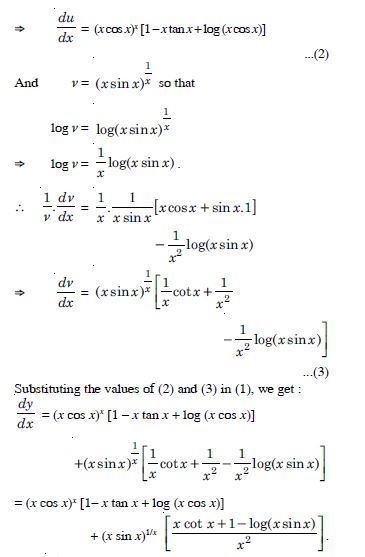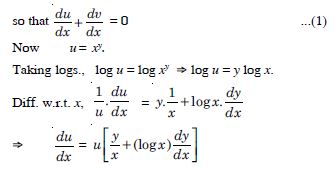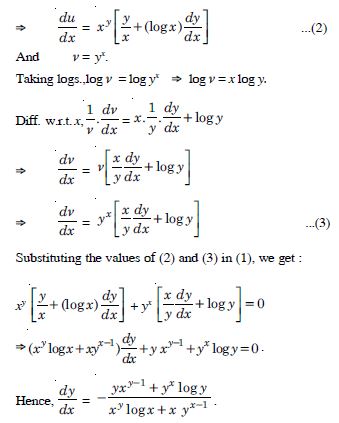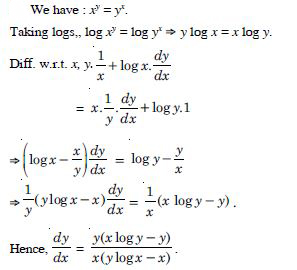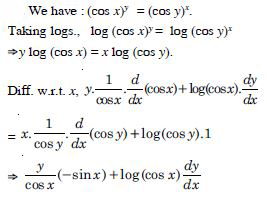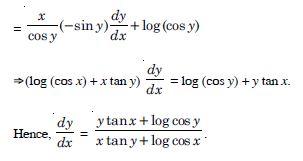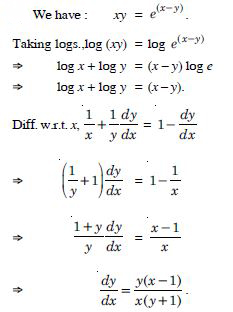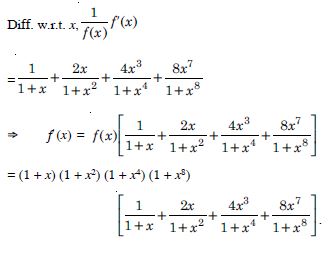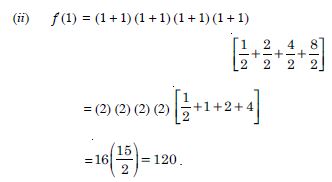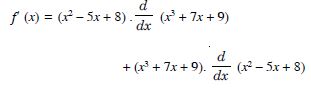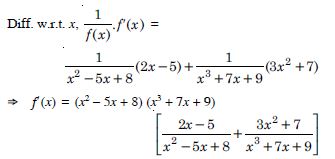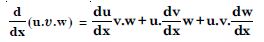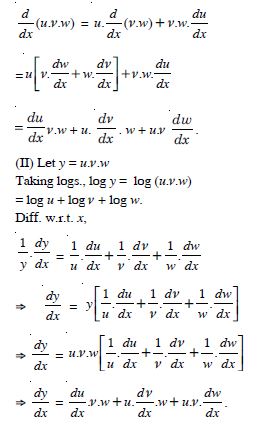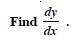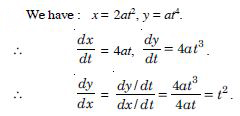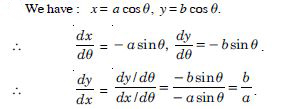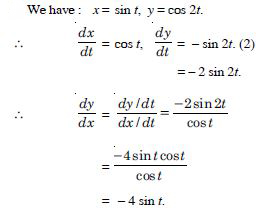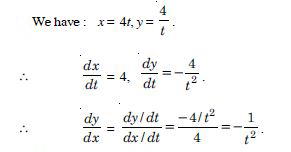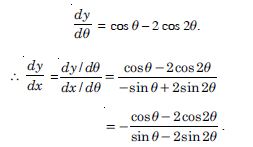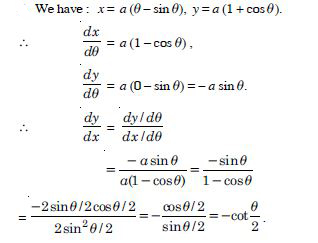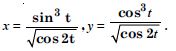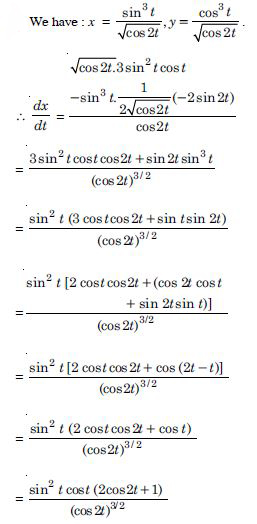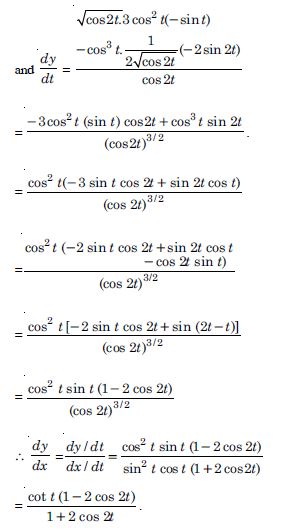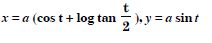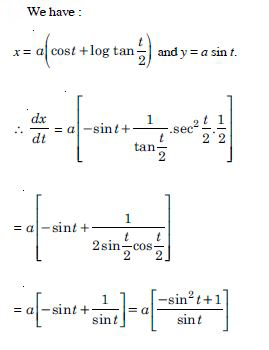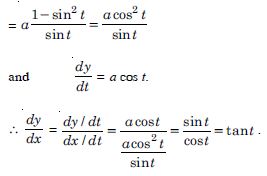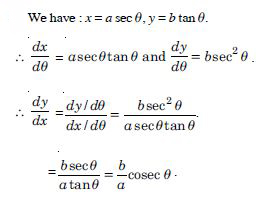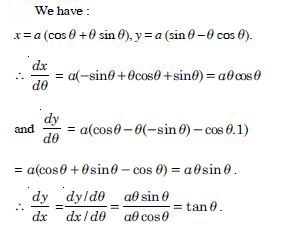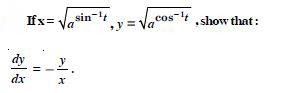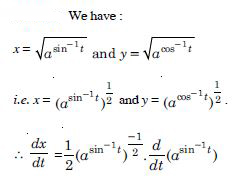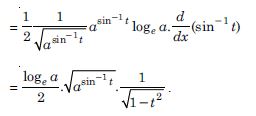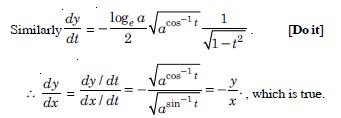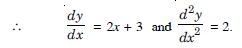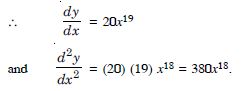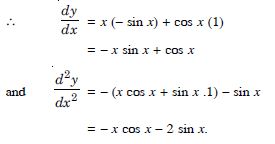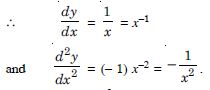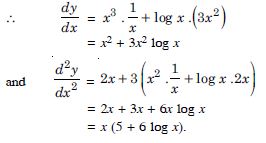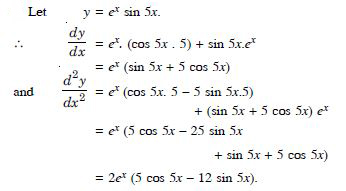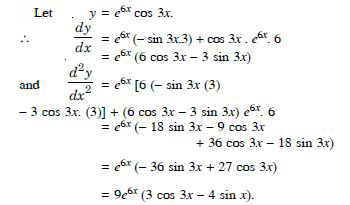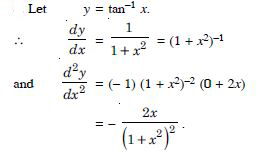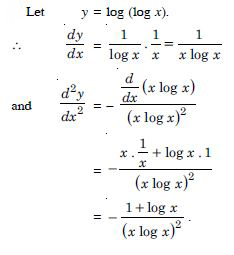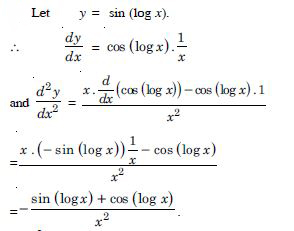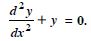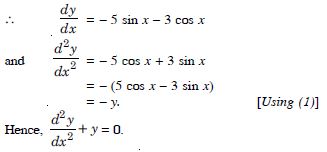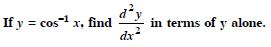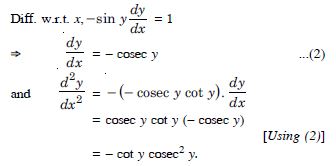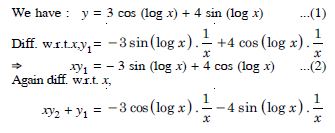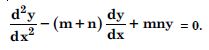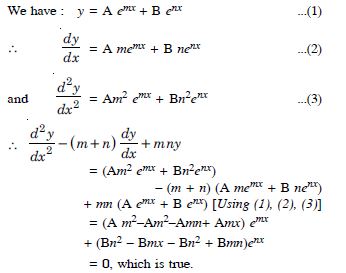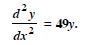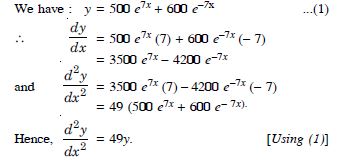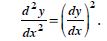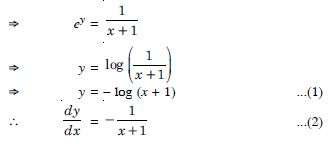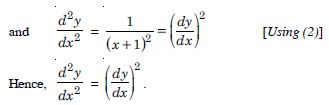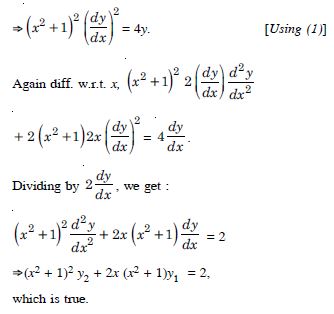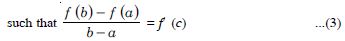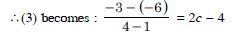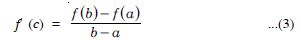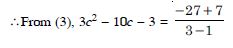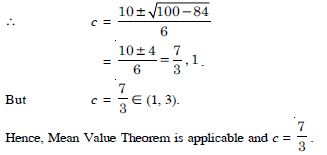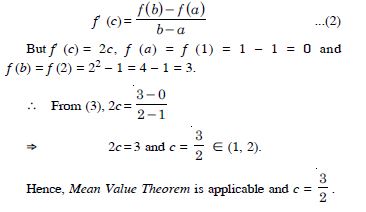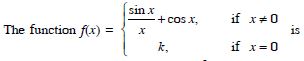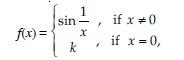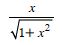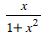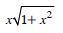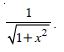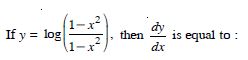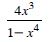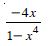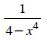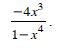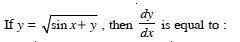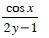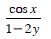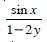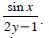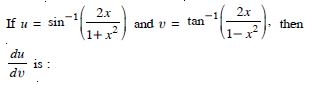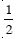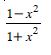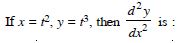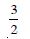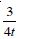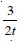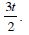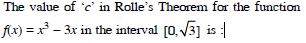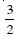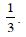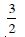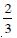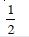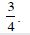NCERT Solutions for Class 12 Mathemetics Chapter 5 - Continuity and Differentiability

Question 1:

Prove that the function f (x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.

Question 2:

Examine the continuity of the function f (x) = 2x² – 1 at x = 3.

Question 3:

Examine the following functions for continuity :
f (x) = x – 5

Question 4:

Examine the following functions for continuity :

Question 5:

Examine the following functions for continuity :

Question 6:

Examine the following functions for continuity :
f (x) = | x – 5|.

Question 7:

Prove that the function f (x) = xⁿ is continuous at x = n, where n is a positive integer.

Question 8:

Is the function ‘f ’ defined by :

continuous at x = 0 ? At x = 1 ? At x = 2 ?

Question 9:

Find all points of discontinuity of ‘f ’, where ‘f ’ is defined by

Question 10:

Find all points of discontinuity of ‘f ’, where ‘f ’ is defined by

Question 11:

Find all points of discontinuity of ‘f ’, where ‘f ’ is defined by

Question 12:

Find all points of discontinuity of ‘f ’, where ‘f ’ is defined by

Question 13:

Find all points of discontinuity of ‘f ’, where ‘f ’ is defined by

Question 14:

Find all points of discontinuity of ‘f ’, where ‘f ’ is defined by

Question 15:

Find all points of discontinuity of ‘f ’, where ‘f ’ is defined by

Question 16:

Is the function defined by :

a continuous function ?

Question 17:

Discuss the continuity of the function ‘f ’, where ‘f ’ is defined by

Question 18:

Discuss the continuity of the function ‘f ’, where ‘f ’ is defined by

Question 19:

Discuss the continuity of the function ‘f ’, where ‘f ’ is defined by

Question 20:

Find the relationship between ‘a’ and ‘b’ so that the function ‘f ’ defined by :

is continuous at x = 3.

Question 21:

For what value of $\mathrm{\lambda }$ is the function :

What about continuity at x = 1 ?

Question 22:

Show that the function defined by g (x) = x – [x] is discontinuous at all integral points.

Question 22:

Is the function defined by
f (x) = x² – sin x + 5 continuous at x = $\mathrm{\pi }$ ?

Question 24:

Discuss the continuity of the following functions :
(a) f (x) = sin x + cos x
(b) f (x) = sin x – cos x
(c) f (x) = sin x . cos x.

Question 25:

Discuss the continuity of the cosine, cosecant, secant and cotangent functions.

Question 26:

Find all points of discontinuity of f, where :

Question 27:

Determine if ‘f’ defined by :

is a continuous function.

Question 28:

Examine the continuity of ‘f ’, where ‘f ’ is defined by :

Question 29:

Find the values of k so that the function ‘f’ is continuous at the indicated point in

Question 30:

Find the values of k so that the function ‘f’ is continuous at the indicated point in

Question 31:

Find the values of k so that the function ‘f’ is continuous at the indicated point in

Question 32:

Find the values of k so that the function ‘f’ is continuous at the indicated point in

Question 33:

Find the values of a and b such that the function defined by :

is a continuous function.

Question 34:

Show that the function defined by f (x) = cos (x²) is a continuous function.

Question 35:

Show that the function defined by f (x) = |cos x| is a continuous function.

Question 36:

Show that sin |x| is a continuous function.

Question 37:

Find all the points of discontinuity of ‘f’ defined by f (x) = |x| – |x + 1|.

Question 38:

Differentiate the following functions with respect to x sin (x² + 5)

Question 39:

Differentiate the following functions with respect to x cos (sin x)

Question 40:

Differentiate the following functions with respect to x sin (ax + b)

Question 41:

Differentiate the following functions with respect to x

Question 42:

Differentiate the following functions with respect to x

Question 43:

Differentiate the following functions with respect to x cos x³. sin² (x⁵)

Question 44:

Differentiate the following functions with respect to x

Question 45:

Differentiate the following functions with respect to x

Question 46:

Prove the function ‘f’ given by :
f (x) = |x – 1|, x $\in$ R
is not differentiable at x = 1.

Question 47:

Prove that the greatest integer function defined by [x], 0 < x < 3 is not differentiable at x = 1 and x = 2.

Question 48:

2x + 3y = sin x

Question 49:

2x + 3y = sin y

Question 50:

ax + by² = cos y

Question 51:

xy + y² = tan x + y

Question 52:

x² + xy + y^{2 = 100}

Question 53:

x³ + x²y + xy² + y³ = 81

Question 54:

sin² y + cos xy = $\mathrm{\pi }$

Question 55:

sin² x + cos² y = 1.

Question 56:

Question 57:

Question 58:

Question 59:

Question 60:

Question 61:

Question 62:

Question 63:

Differentiate the following w.r.t. x :

Question 64:

Differentiate the following w.r.t. x :

Question 65:

Differentiate the following w.r.t. x :

Question 66:

Differentiate the following w.r.t. x :
sin (tan^–1 e^–x

Question 67:

Differentiate the following w.r.t. x :
log (cos e^x)

Question 68:

Differentiate the following w.r.t. x :

Question 69:

Differentiate the following w.r.t. x :

Question 70:

Differentiate the following w.r.t. x :
log (log x), x > 1

Question 71:

Differentiate the following w.r.t. x :

Question 72:

Differentiate the following w.r.t. x :
cos (log x + e^x), x > 0.

Question 73:

Differentiate the functions given in w.r.t. x :
cos x. cos 2x. cos 3x.

Question 74:

Differentiate the functions given in w.r.t. x :

Question 75:

Differentiate the functions given in w.r.t. x :
(log x)cos x.

Question 76:

Differentiate the functions given in w.r.t. x :
xx – 2sin x

Question 77:

Differentiate the functions given in w.r.t. x :
(x + 3)2.(x + 4)3.(x + 5)4.

Question 78:

Differentiate the functions given in w.r.t. x :

Question 79:

Differentiate the functions given in w.r.t. x :
(log x )^x + xlog x

Question 80:

Differentiate the functions given in w.r.t. x :

Question 81:

Differentiate the functions given in w.r.t. x :
xsin x + (sin x)cosx

Question 82:

Differentiate the functions given in w.r.t. x :

Question 83:

Differentiate the functions given in w.r.t. x :

Question 84:

x^y + y^x = 1.

Question 85:

y^x = x^y.

Question 86:

(cos x)^y = (cos y)^x.

Question 87:

xy = e^{(x – y)}.

Question 88:

Find the derivative of the function given by :
f (x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸) and hence find f ′ (1).

Question 89:

Differentiate (x² – 5x + 8) (x³ + 7x + 9) in three ways
mentioned below :
(i) by using product rule
(ii) by expanding the product to obtain a single polynomial
(iii) by logarithmic differentiation.
Do they give the same answer ?

Question 90:

If u, ν, w are differentiable functions of x, then show that :

in two ways by repeated application of product rule, second by logarithmic differentiation.

Question 91:

If x and y are connected parametrically by the equations given below without eliminating the parameters.

x = 2at², y = at⁴.

Question 92:

If x and y are connected parametrically by the equations given below without eliminating the parameters.

x = a cos $\mathrm{\theta }$, y = b cos $\mathrm{\theta }$.

Question 93:

If x and y are connected parametrically by the equations given below without eliminating the parameters.

x = sin t, y = cos 2t.

Question 94:

If x and y are connected parametrically by the equations given below without eliminating the parameters.

Question 95:

If x and y are connected parametrically by the equations given below without eliminating the parameters.

x = cos $\mathrm{\theta }$ – cos 2$\mathrm{\theta }$, y = sin $\mathrm{\theta }$ – sin 2$\mathrm{\theta }$.

Question 96:

If x and y are connected parametrically by the equations given below without eliminating the parameters.

x = a ($\mathrm{\theta }$ – sin $\mathrm{\theta }$), y = a (1 + cos $\mathrm{\theta }$).

Question 97:

If x and y are connected parametrically by the equations given below without eliminating the parameters.

Question 98:

If x and y are connected parametrically by the equations given in without eliminating the parameters.

Question 99:

If x and y are connected parametrically by the equations given in without eliminating the parameters.

x = a sec $\mathrm{\theta }$ , y = b tan $\mathrm{\theta }$.

Question 100:

If x and y are connected parametrically by the equations given in without eliminating the parameters.

x = a (cos $\mathrm{\theta }$ + $\mathrm{\theta }$ sin $\mathrm{\theta }$), y = a (sin $\mathrm{\theta }$ – $\mathrm{\theta }$ cos $\mathrm{\theta }$).

Question 101:

Question 102:

Find the second order derivative of the functions given in x² + 3x + 2

Question 103:

Find the second order derivative of the functions given in x²⁰

Question 104:

Find the second order derivative of the functions given in x cos x

Question 105:

Find the second order derivative of the functions given in log x

Question 106:

Find the second order derivative of the functions given in x³ log x

Question 107:

Find the second order derivative of the functions given in e^x sin 5x

Question 108:

Find the second order derivative of the functions given in e^6x cos 3x

Question 109:

Find the second order derivative of the functions given in tan–¹ x

Question 110:

Find the second order derivative of the functions given in log (log x)

Question 111:

Find the second order derivative of the functions given in sin (log x).

Question 112:

If = 5 cos x – 3 sin x, prove that :

Question 113:

Question 114:

If y = 3 cos (log x) + 4 sin (log x), show that :
x₂y₂ + y₁ + y = 0.

Question 115:

If y = A emx + B enx, show that :

Question 116:

If y = 500 e7x + 600 e–7xm, show that :

Question 117:

If ey (x + 1) = 1, show that :

Question 118:

If y = (tan^–1 x)², show that :
(x² + 1)² y₂ + 2x (x² + 1) y₁ = 2.

Question 119:

Verify Rolle’s theorem for the function :
f (x) = x2 ^{+ 2x – 8, x $\in$ [– 4, 2].}

Question 120:

Examine if Rolle’s theorem is applicable to any of the following functions. Can you say something about the converse of Rolle’s theorem from these examples ?
(i) f (x) = [x] for x $\in$ [5, 9]
(ii) f (x) = [x] for x $\in$ [– 2, 2]
(iii) f (x) = x2 – 1 for x $\in$ [1, 2].

Question 121:

If f : [– 5, 5] $\to$ R is differentiable function and if f′ (x) does not vanish anywhere, then prove that f (– 5) $\ne$ f (5).

Question 122:

Verify Mean Value Theorem. if f (x) = x² – 4x – 3 in the interval [a, b], where a = 1 and b = 4.

Question 123:

Verify Mean Value Theorem if :
f (x) = x³ – 5x² – 3x in the interval [a, b], where
a = 1 and b = 3. Find all c $\in$ (1, 3) for which f ′(c) = 0.

Question 124:

Examine the applicability of Mean Value Theorem for the following functions :
(i) f (x) = [x] for x $\in$ [5, 9]
(ii) f (x) = [x] for x $\in$ [– 2, 2]
(iii) f (x) = x² – 1 for x $\in$ [1, 2].

Question 125:

continuous at x = 0, then the value of ‘k’ is:

1. 3
2. 2
3. 1
4. 1.5

Question 126:

The function f(x) = [x], where [x] denotes the greatest integer function, is continuous at :

1. 4
2. –2
3. 1
4. 1.5

Question 127:

The value of ‘k’ which makes the function defined by :

continuous at x = 0 is :

1. 8
2. 3
3. –1
4. None of these

Question 128:

Differential coefficient of sec (tan^–1 x) w.r.t. x is :

Question 129:

Question 130:

Question 131:

1. 

2. x

3. 

4. 1

Question 132:

Question 133:

1. 1
2. -1

3. 

4. 

Question 134:

The value of ‘c’ in Mean Value Theorem for the function f(x) = x (x – 2), x $\in$ [1, 2] is :