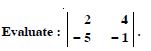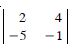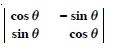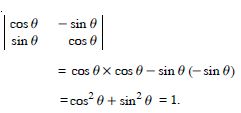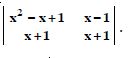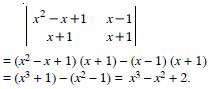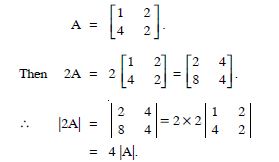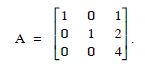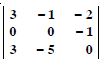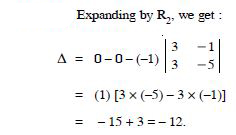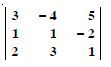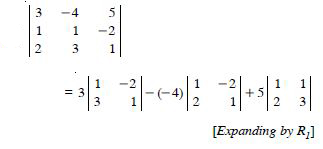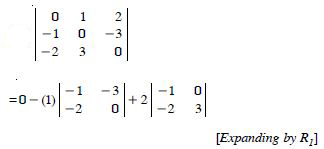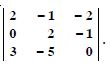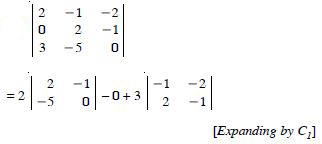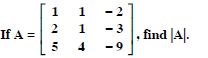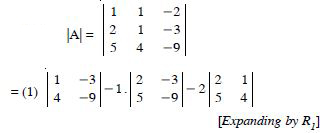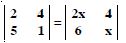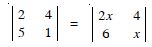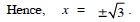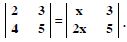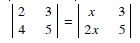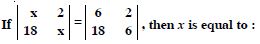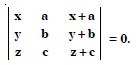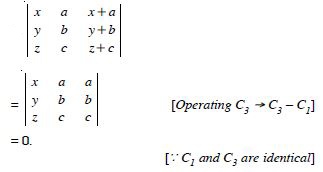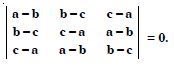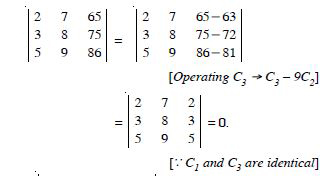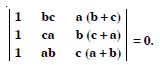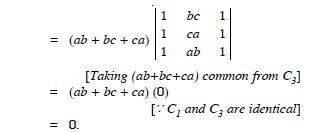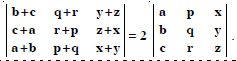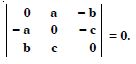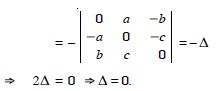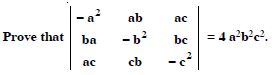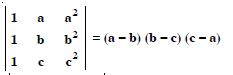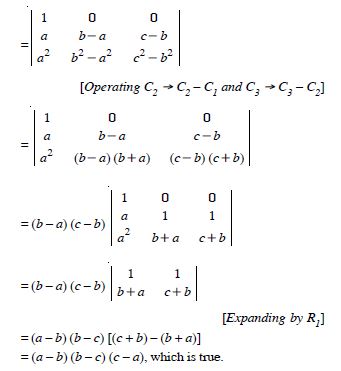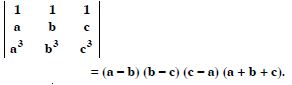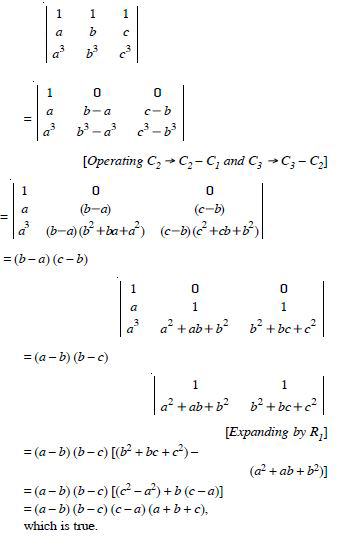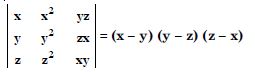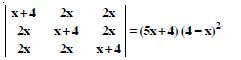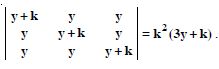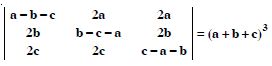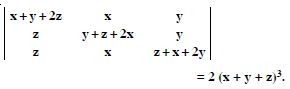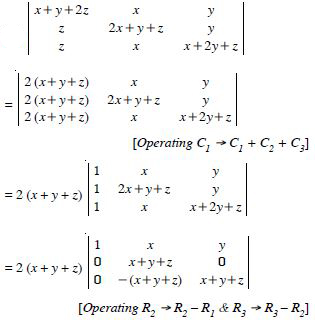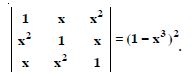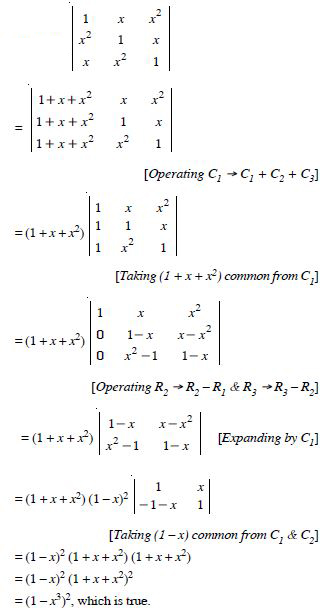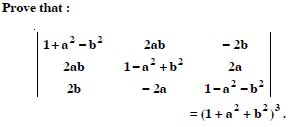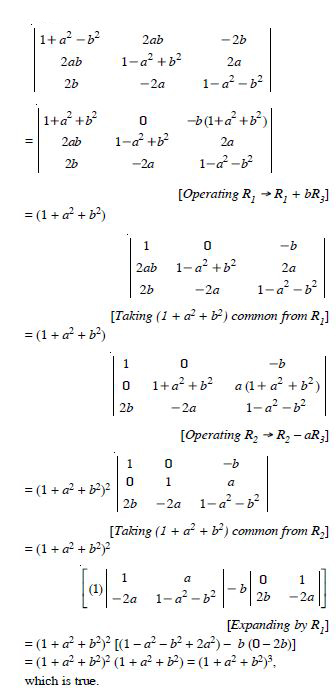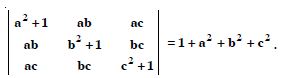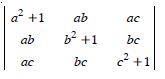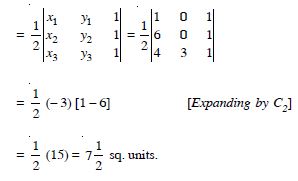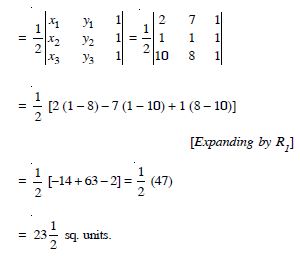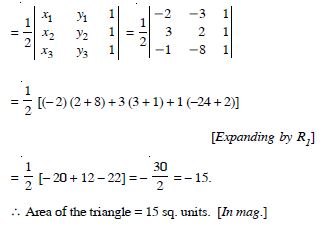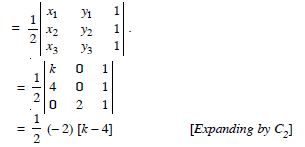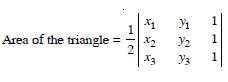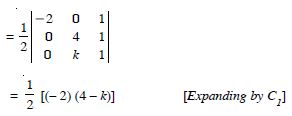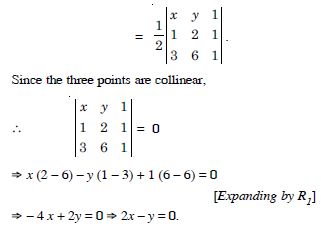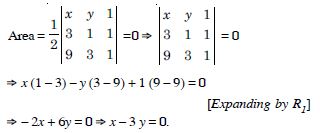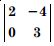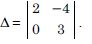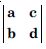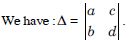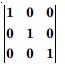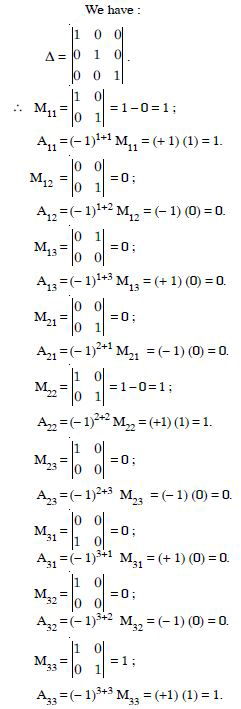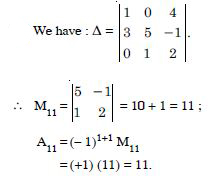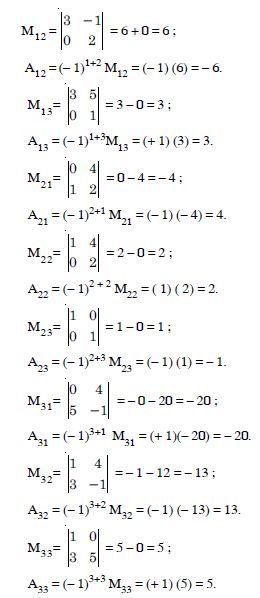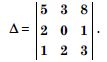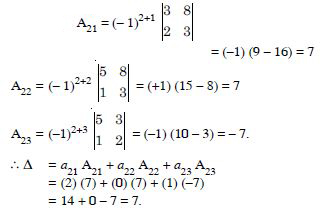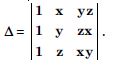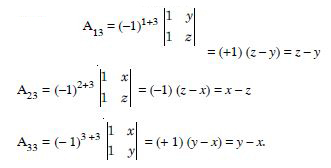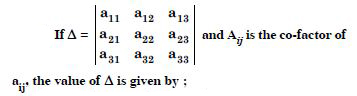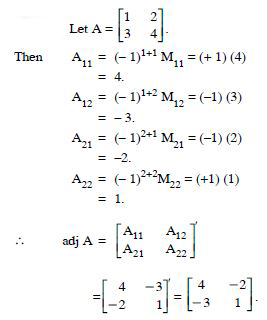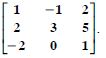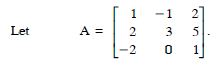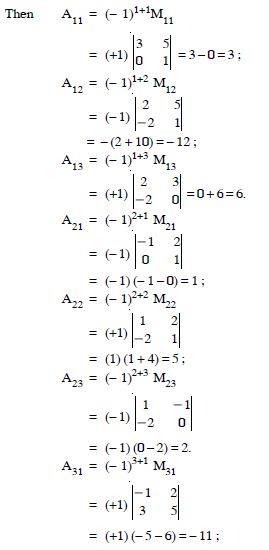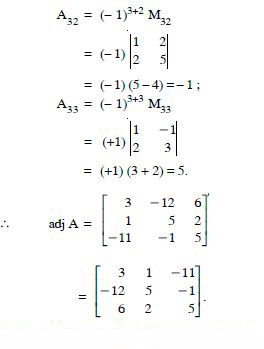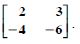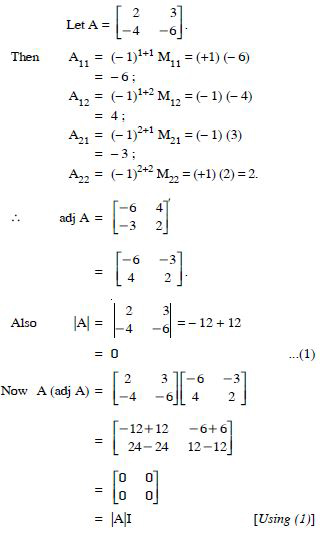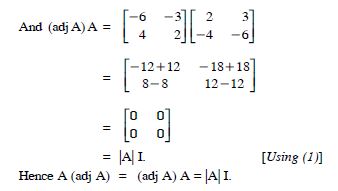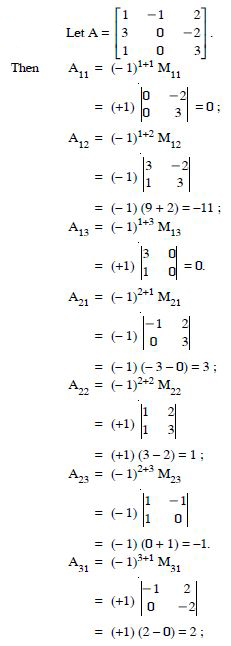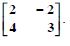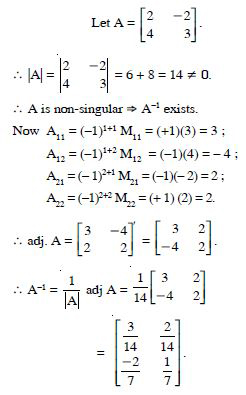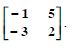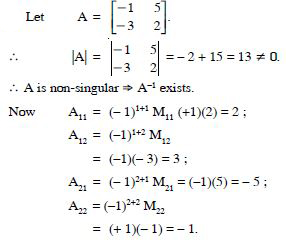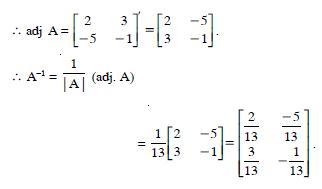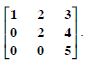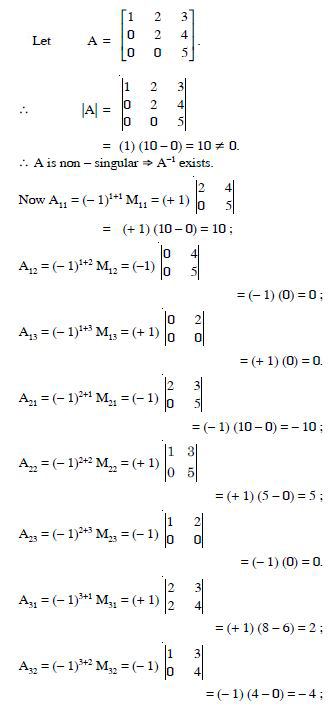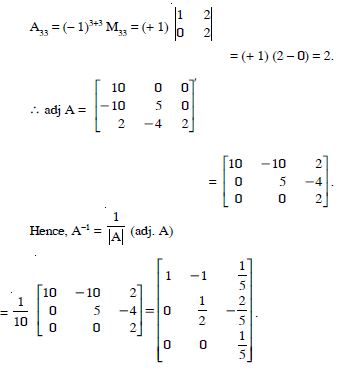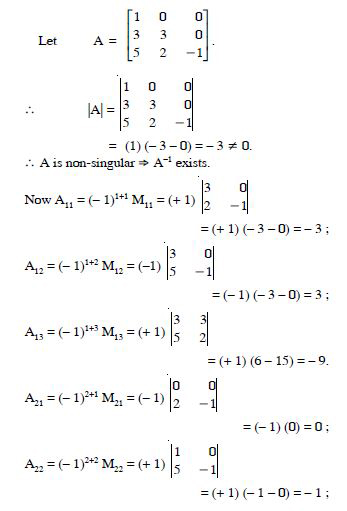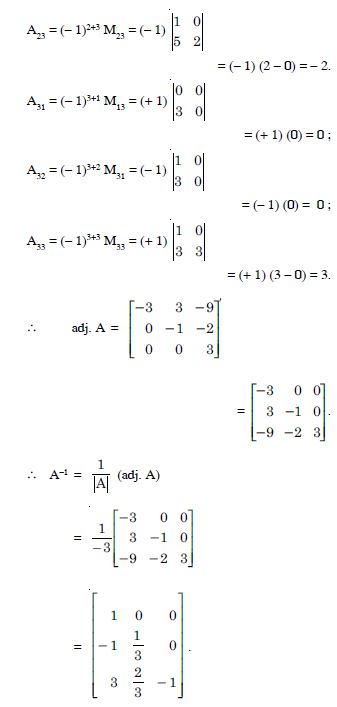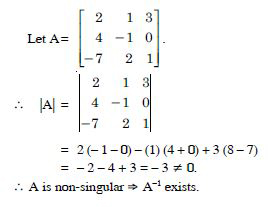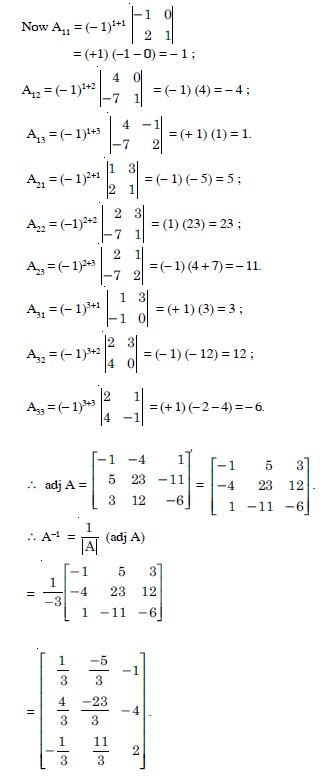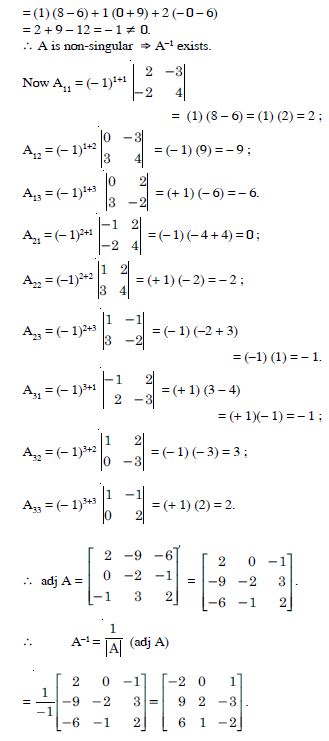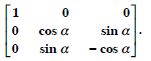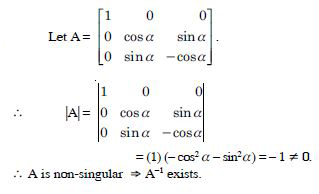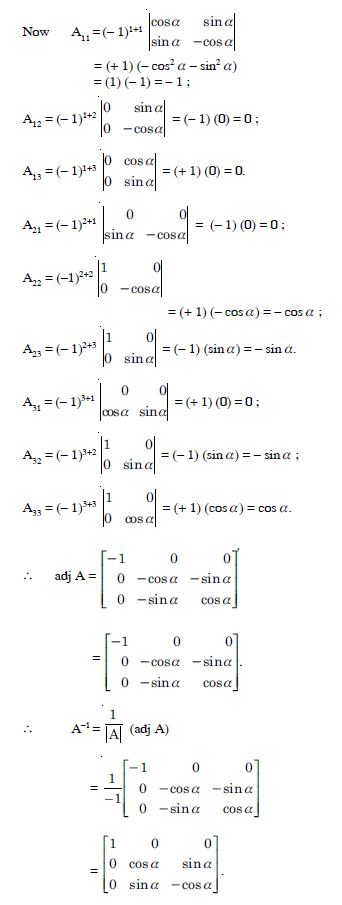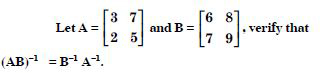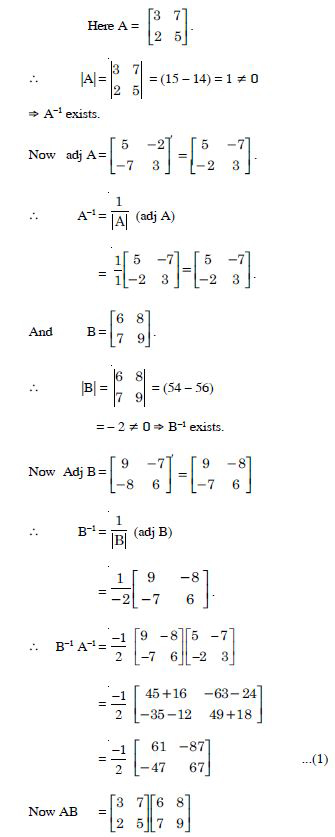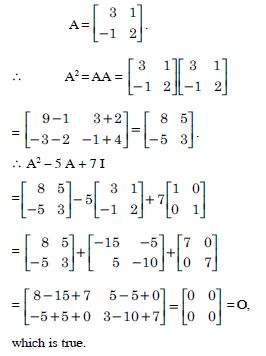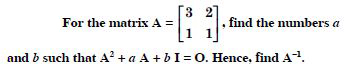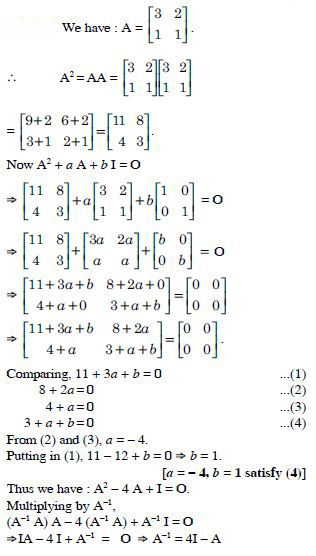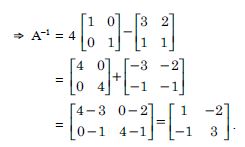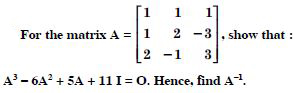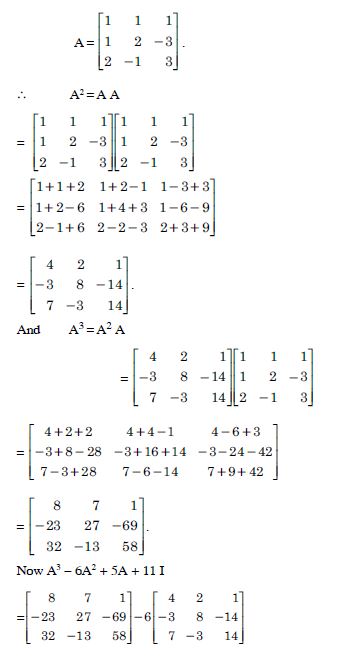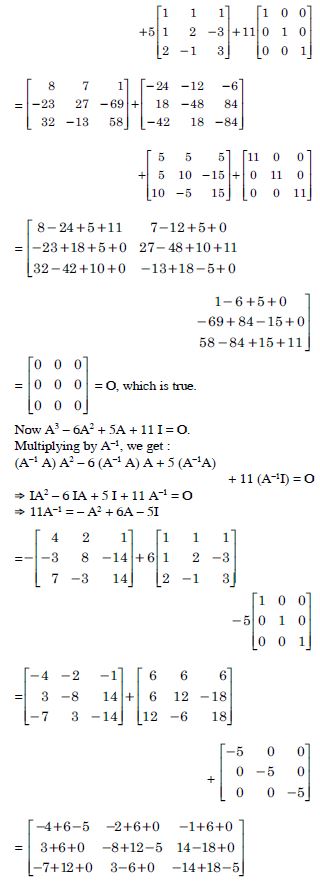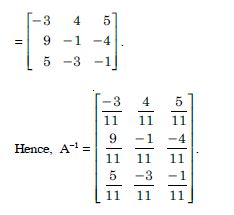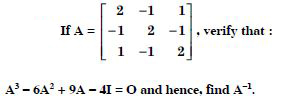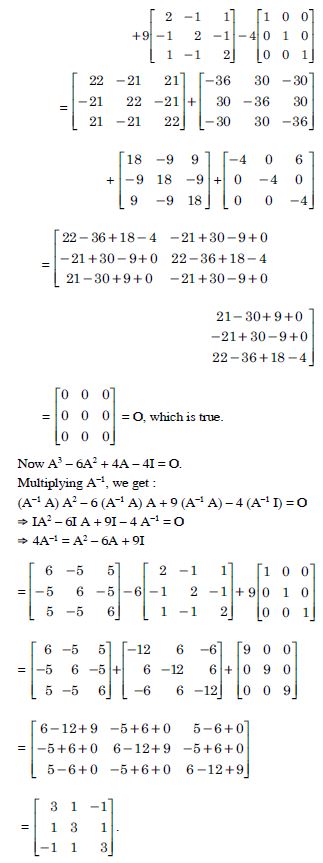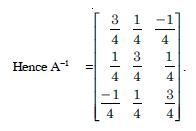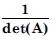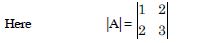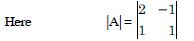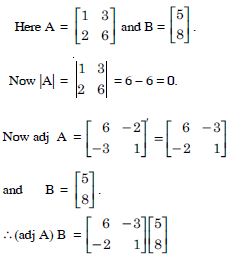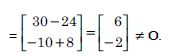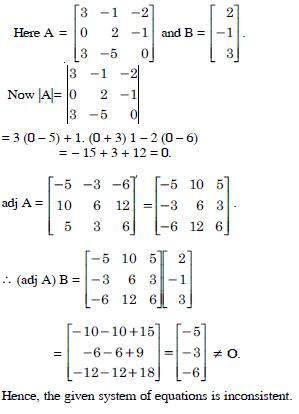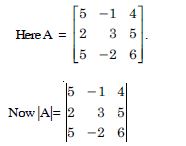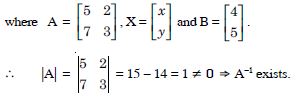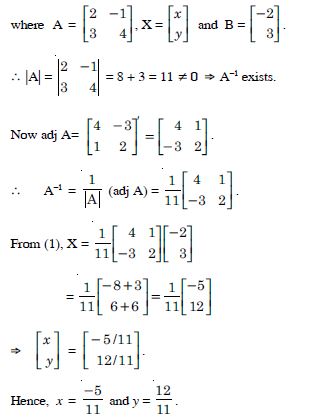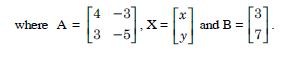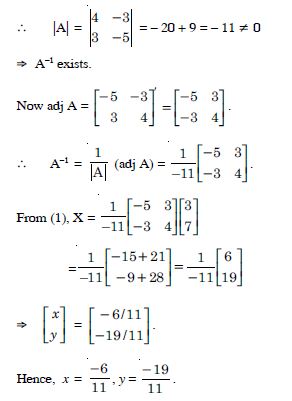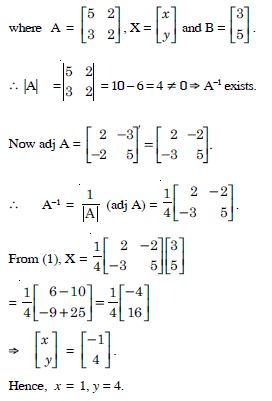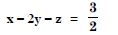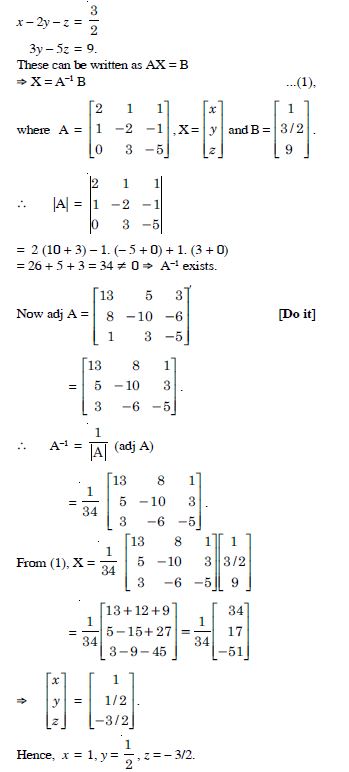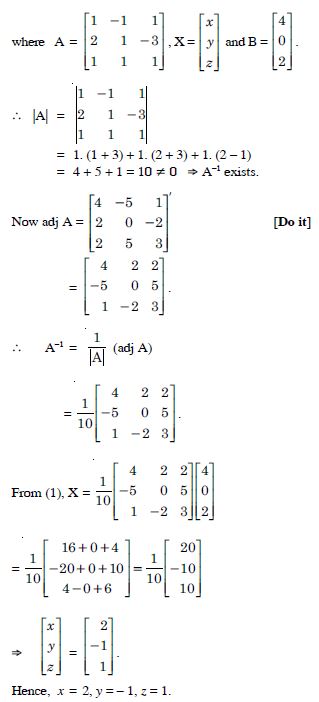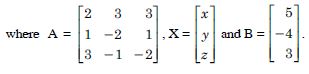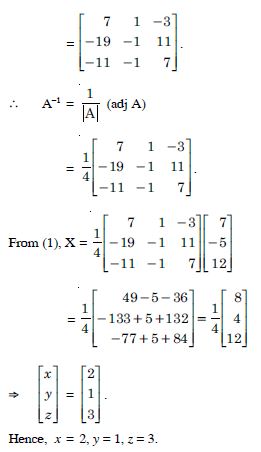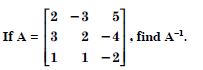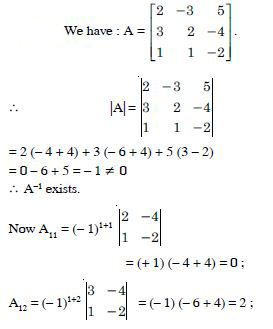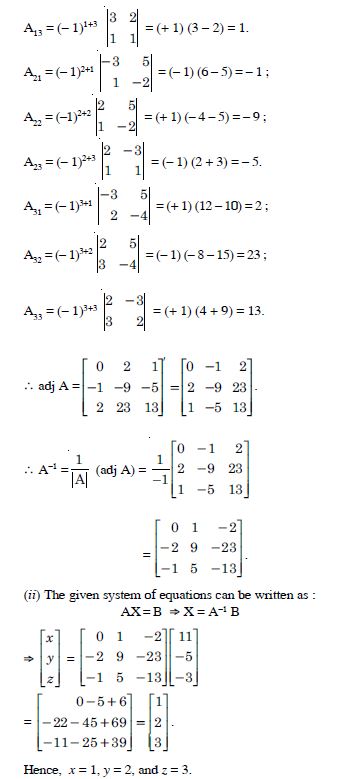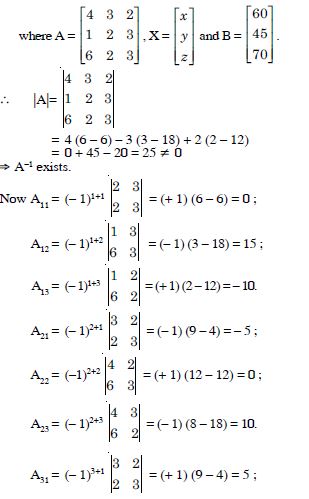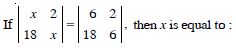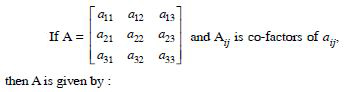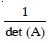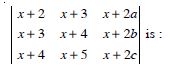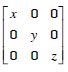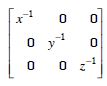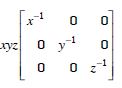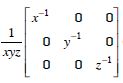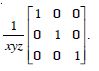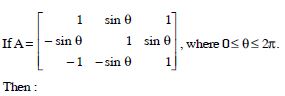NCERT Solutions for Class 12 Mathemetics Chapter 4 - Determinants

Question 1:

Question 2:

Evaluate

Question 3:

Evaluate

Question 4:

Question 5:

Question 6:

Evaluate the determinants :

Question 7:

Evaluate the determinants :

Question 8:

Evaluate the determinants :

Question 9:

Evaluate the determinants :

Question 10:

Question 11:

Find values of x, if :

Question 12:

Find values of x, if :

Question 13:

1. 6
2. $\pm$ 6
3. - 6
4. 0

Question 14:

Using the property of determinants and without expanding prove that :

Question 15:

Using the property of determinants and without expanding prove that :

Question 16:

Using the property of determinants and without expanding prove that :

Question 17:

Using the property of determinants and without expanding prove that :

Question 18:

Using the property of determinants and without expanding prove that :

Question 19:

Using the property of determinants and without expanding prove that :

Question 20:

Using properties of determinants, prove the following

Question 21:

Prove that :

Question 22:

Prove that :

Question 23:

Prove that :

(xy + yz + zx).

Question 24:

Prove that :

Question 25:

Prove that :

Question 26:

Prove that :

Question 27:

Prove that :

Question 28:

Prove that :

Question 29:

Question 30:

Prove that :

Question 31:

Choose the correct answer
Let A be a square matrix of order 3 × 3, then |k A| is equal to :

1. k |A|
2. k²
3. |A|
4. 3k |A|

Question 32:

Choose the correct answer Which of the following is correct :

1. Determinant is a square matrix.
2. Determinant is a number associated to a matrix.
3. Determinant is a number associated to a square matrix.
4. None of these.

Question 33:

Find area of the triangle with vertices at the points given in each of the following :
(1, 0), (6, 0), (4, 3)

Question 34:

Find area of the triangle with vertices at the points given in each of the following :
(2, 7), (1,1), (10, 8)

Question 35:

Find area of the triangle with vertices at the points given in each of the following :
(-2, -3), (3, 2), (-1, -8).

Question 36:

Show that the points :
A (a, b + c), B (b, c + a), C (c, a + b) are collinear.

Question 37:

Find the values of ‘k’ if area of triangle is 4 sq. units and vertices are :
(k, 0), (4, 0), (0, 2)

Question 38:

Find the values of ‘k’ if area of triangle is 4 sq. units and vertices are :
(-2, 0), (0, 4), (0, k)

Question 39:

Find the equation of line joining (1, 2) and (3, 6), using determinants.

Question 40:

Find the equation of line joining (3, 1) and (9, 3) using determinants.

Question 41:

If area of triangle is 35 sq. units with vertices (2, - 6), (5, 4) and (k, 4), then k is :

1. 12
2. - 2
3. - 12, - 2
4. 12, - 2.

Question 42:

Write minors and co-factors of the elements of the following determinants :

Question 43:

Write minors and co-factors of the elements of the following determinants :

Question 44:

Write minors and co-factors of the elements of the following determinants :

Question 45:

Write minors and co-factors of the elements of the following determinants :

Question 46:

Using co-factors of elements of second row, evaluate :

Question 47:

Using co-factors of third column, evaluate :

Question 48:

1. a₁₁ A₁₁ + a₁₂ A₃₂ + a₁₃ A₃₃
2. a₁₁ A₁₁ + a₁₂ A₂₁ + a₁₃ A₃₁
3. a₂₁ A₁₁ + a₂₂ A₁₂ + a₂₃ A₁₃
4. a₁₁ A₁₁ + a₂₁ A₂₁ + a₃₁ A₃₁

Question 49:

Find the adjoint of the matrices

Question 50:

Find the adjoint of the matrices

Question 51:

Verify A (Adj A) = (Adj A) A = |A| I

Question 52:

Verify A (Adj A) = (Adj A) A = |A| I

Question 53:

Find the inverse of each of the matrices (if it exists) given in

Question 54:

Find the inverse of each of the matrices (if it exists) given in

Question 55:

Find the inverse of each of the matrices (if it exists) given in

Question 56:

Find the inverse of each of the matrices (if it exists) given in

Question 57:

Find the inverse of each of the matrices (if it exists) given in

Question 58:

Find the inverse of each of the matrices (if it exists) given in

Question 59:

Find the inverse of each of the matrices (if it exists) given in

Question 60:

Question 61:

Question 62:

Question 63:

Question 64:

Question 65:

Let A be non-singular square matrix of order 3 × 3. Then |adj A| is equal to :

1. |A|
2. |A|²
3. |A|³
4. 3|A|

Question 66:

If A is an invertible matrix of order 2, then det. (A–¹) is equal to :

1. det (A)

2. 

3. 1
4. 0

Question 67:

Classify the following system of equations as consistent or inconsistent :
x + 2y = 2
2x + 3y = 3.

Question 68:

Classify the following system of equations as consistent or inconsistent :
2x – y = 5
x + y = 4.

Question 69:

Classify the following system of equations as consistent or inconsistent :
x + 3y = 5
2x + 6y = 8.

Question 70:

Classify the following system of equations as consistent or inconsistent :
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4.

Question 71:

Classify the following system of equations as consistent or inconsistent :
3x – y – 2z = 2
2y – z = – 1
3x – 5y = 3.

Question 72:

Classify the following system of equations as consistent or inconsistent :
5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = – 1.

Question 73:

Solve system of linear equations, using matrix method
5x + 2y = 4
7x + 3y = 5.

Question 74:

Solve system of linear equations, using matrix method
2x – y = – 2
3x + 4y = 3.

Question 75:

Solve system of linear equations, using matrix method
4x – 3y = 3
3x – 5y = 7.

Question 76:

Solve system of linear equations, using matrix method
5x + 2y = 3
3x + 2y = 5.

Question 77:

Solve system of linear equations, using matrix method
2x + y + z = 1

3y – 5z = 9.

Question 78:

Solve system of linear equations, using matrix method
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2.

Question 79:

Solve system of linear equations, using matrix method
2x + 3y + 3z = 5
x – 2y + z = – 4
3x – y – 2z = 3.

Question 80:

Solve system of linear equations, using matrix method
x – y + 2z = 7
3x + 4y – 5z = – 5
2x – y + 3z = 12.

Question 81:

Using A^–1, solve the system of equations :
2x – 3y + 5z=11
3x + 2y – 4z=– 5
x + y – 2z = – 3.

Question 82:

The cost of 4 kg onion, 3 kg wheat and 2 kg rice is ₹ 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is ₹ 90.
The cost of 6 kg onion, 2 kg. wheat and 3 kg rice is ₹ 70. Find cost of each item per kg by matrix method.

Question 83:

1. 6
2. ± 6
3. – 6
4. 6, 6

Question 84:

Let A be a square matrix of order 3 × 3. Then | kA | is equal to :

1. k | A |
2. k² | A |
3. k³ | A |
4. 3k | A |

Question 85:

Which of the following is correct?

1. Determinant is a square
2. Determinant is a number associated to a matrix
3. Determinant is a number associated to a square matrix
4. None of these

Question 86:

If area of triangle is 35 sq. units with vertices (2, – 6), (5, 4) and (k, 4). Then k is :

1. 12
2. – 2
3. – 12, – 2
4. 12, – 2

Question 87:

1. a₁₁A₃₁ + a₁₂A₃₂ + a₁₃A₃₃
2. a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₃
3. a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃
4. a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁

Question 88:

Let A be a non-singular matrix of order 3 × 3. Then | adj. A | is equal to :

1. | A |
2. | A |²
3. | A |³
4. 3 | A |

Question 89:

If A is an invertible matrix of order 2, then det (A^–1) is equal to :

1. det (A)

2. 

3. 1
4. 0

Question 90:

If a, b, c are in A.P., then determinant :

1. 0
2. 1
3. x
4. 2x

Question 91:

If x, y, z are non-zero real numbers, then the inverse of matrix A =

is :

Question 92:

1. Det (A) = 0
2. Det (A)$\in$ (2,$\infty$ )
3. Det (A) $\in$ (2, 4)
4. Det (A) $\in$ [2, 4].