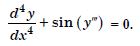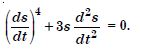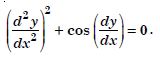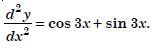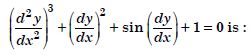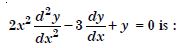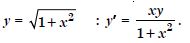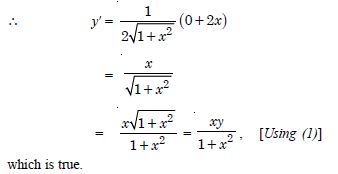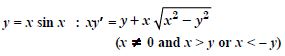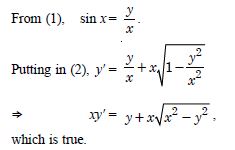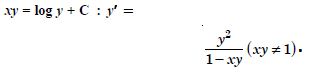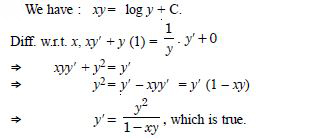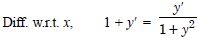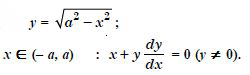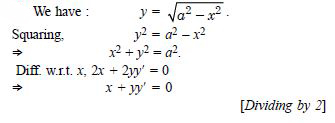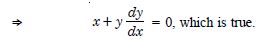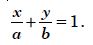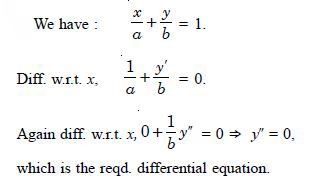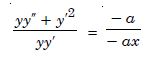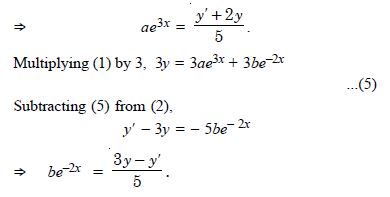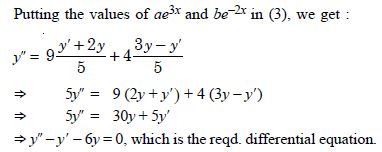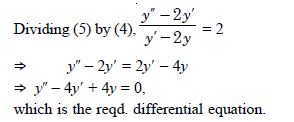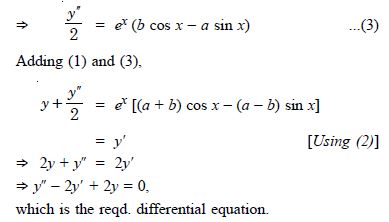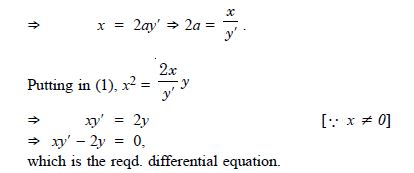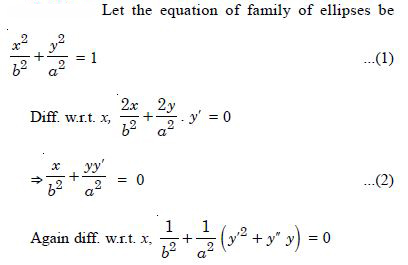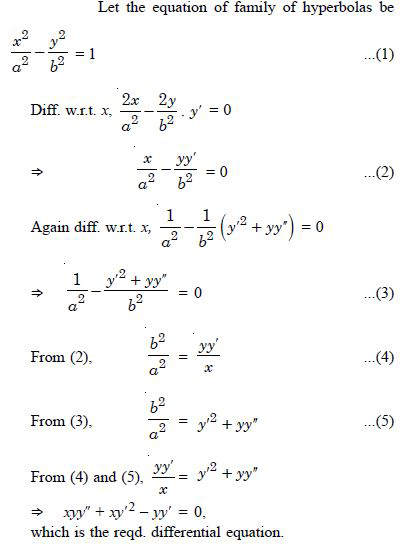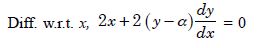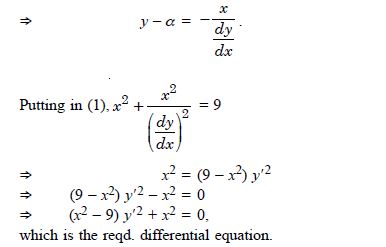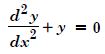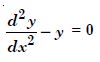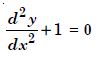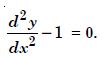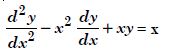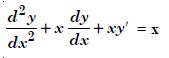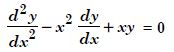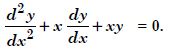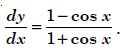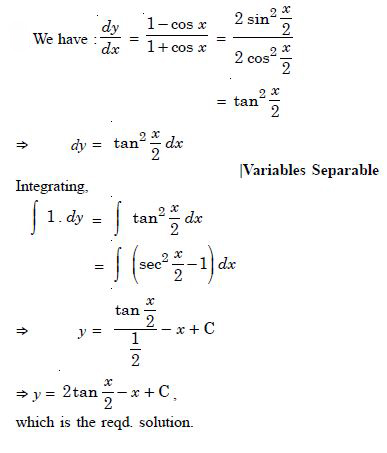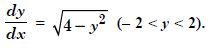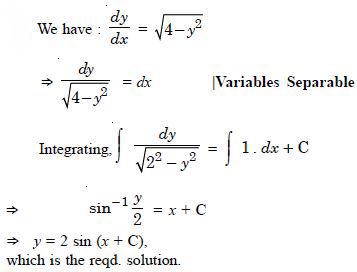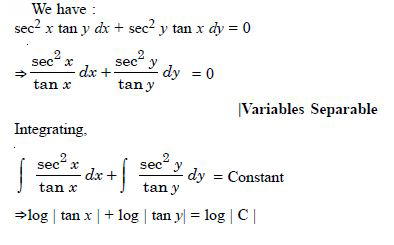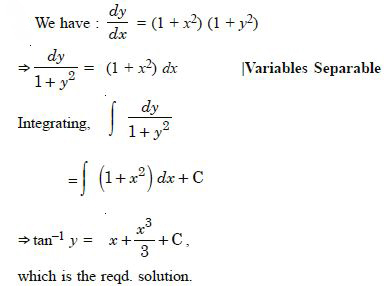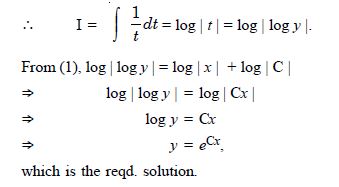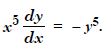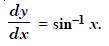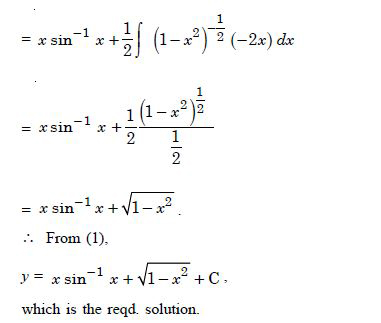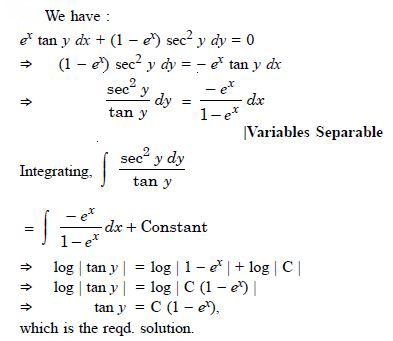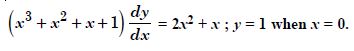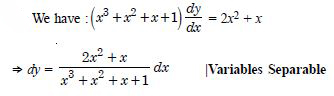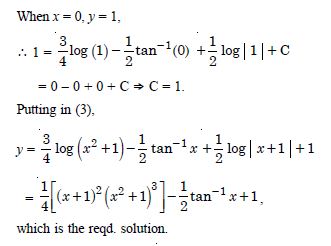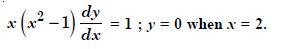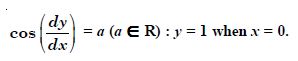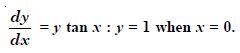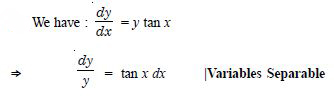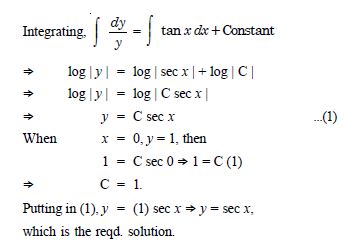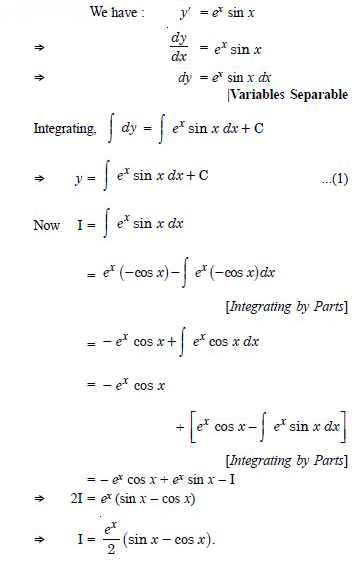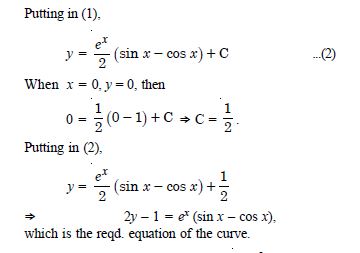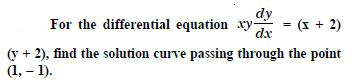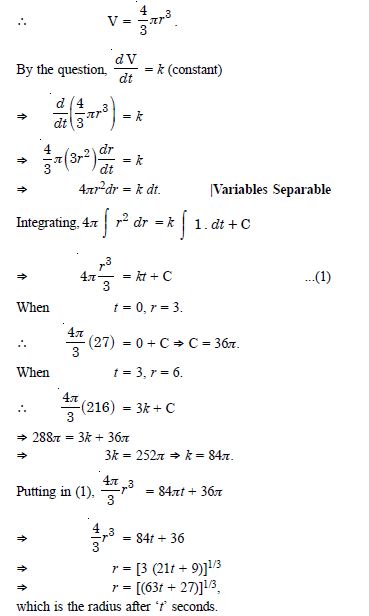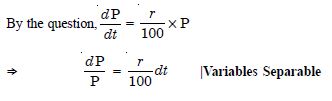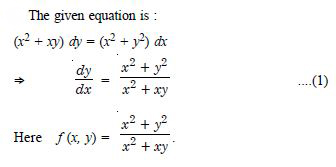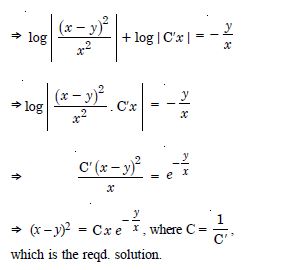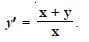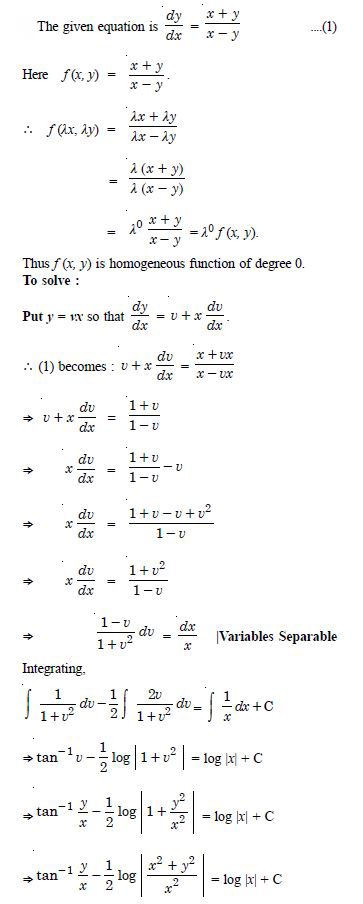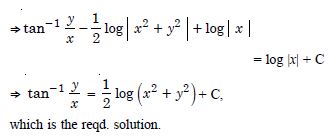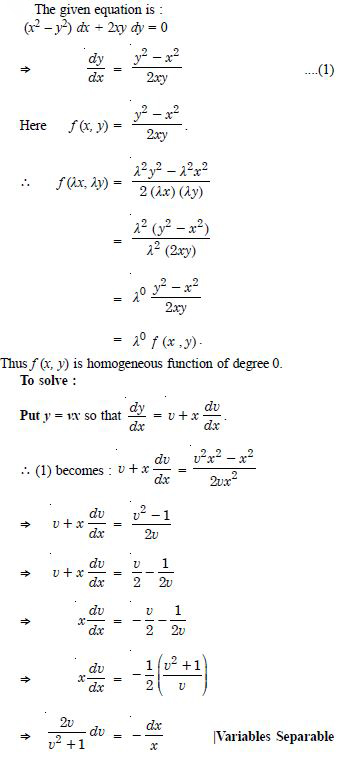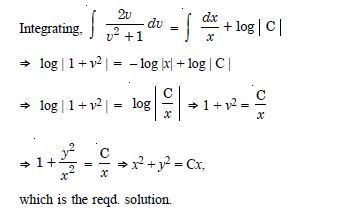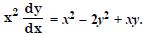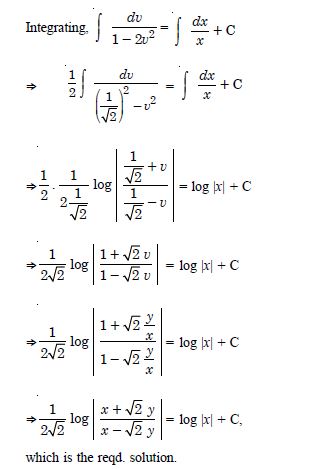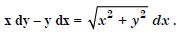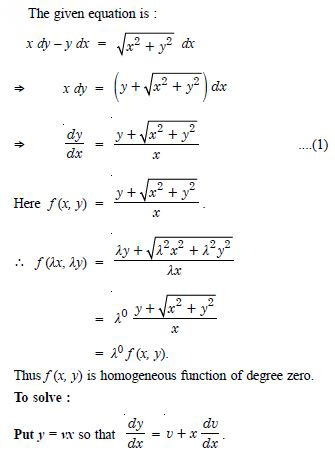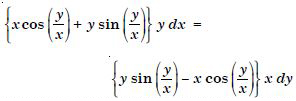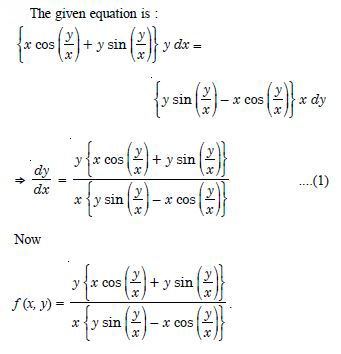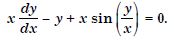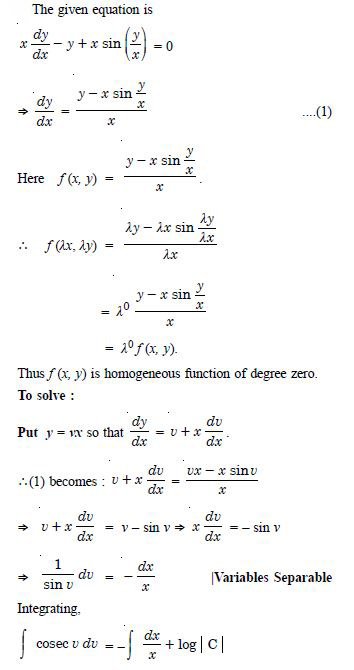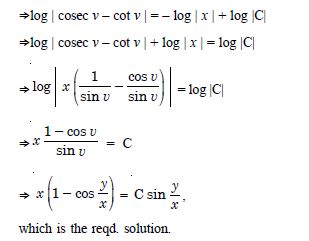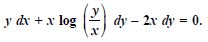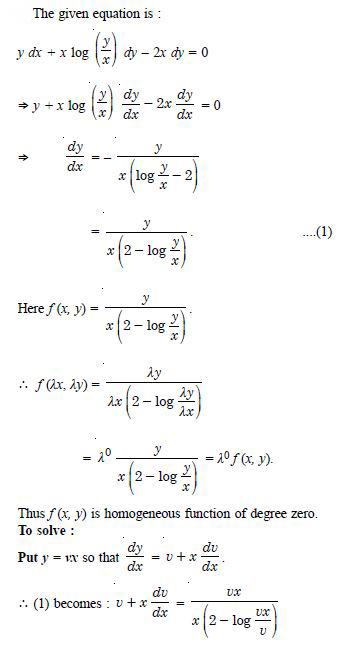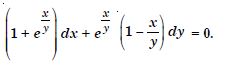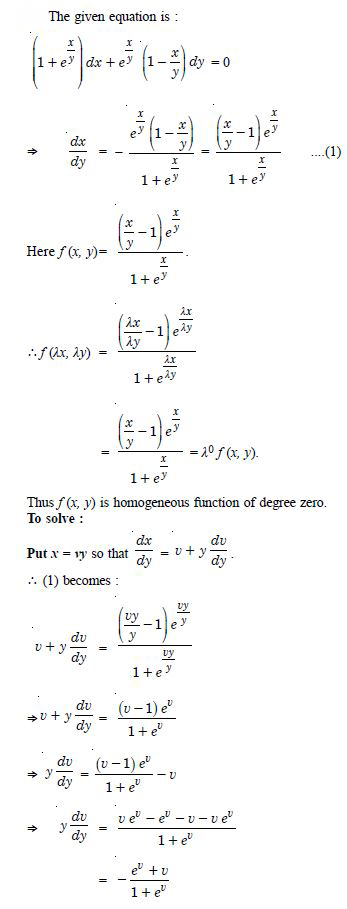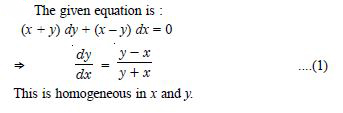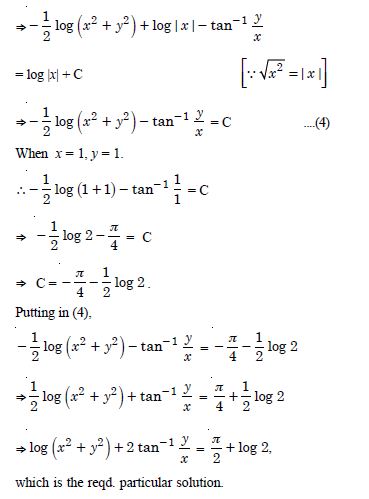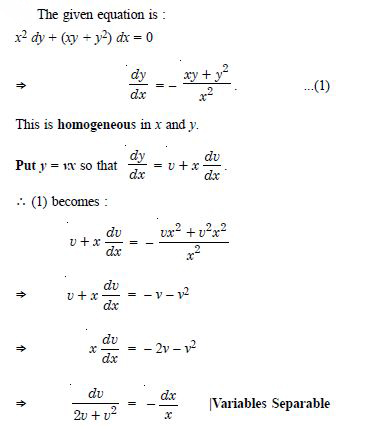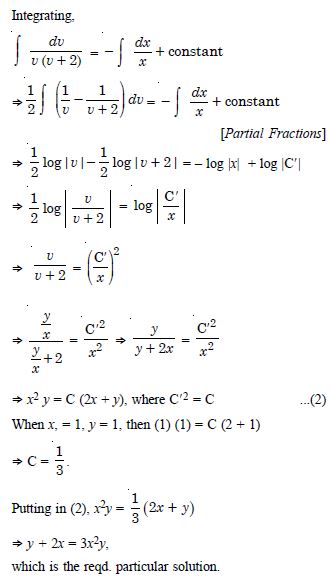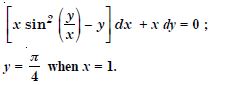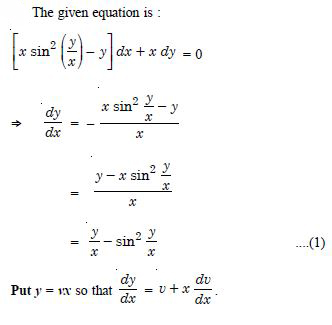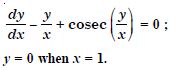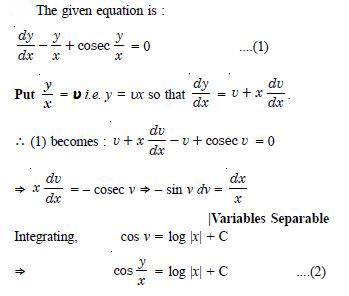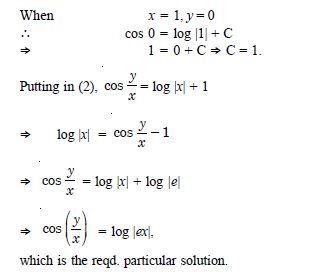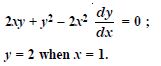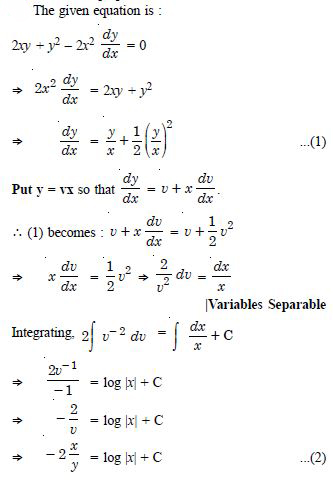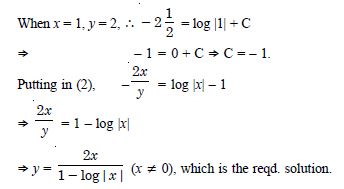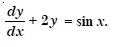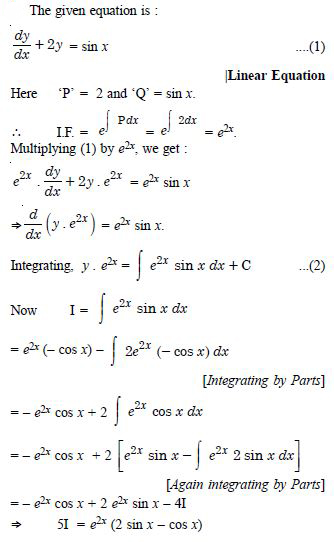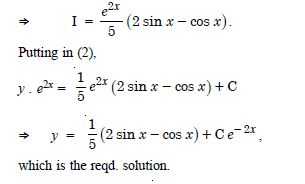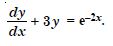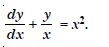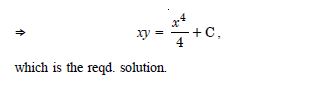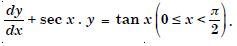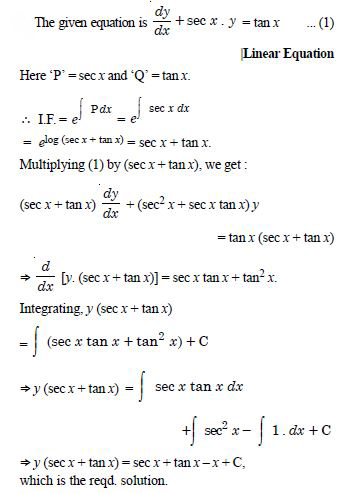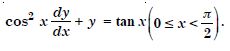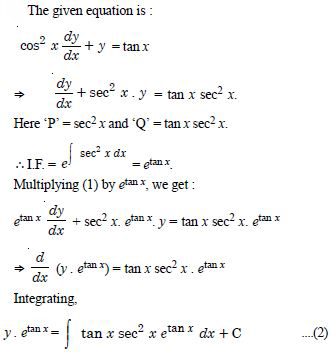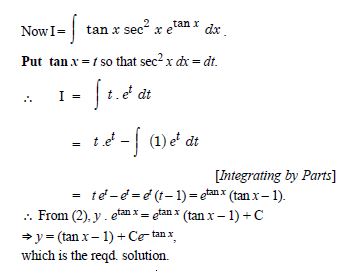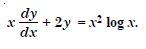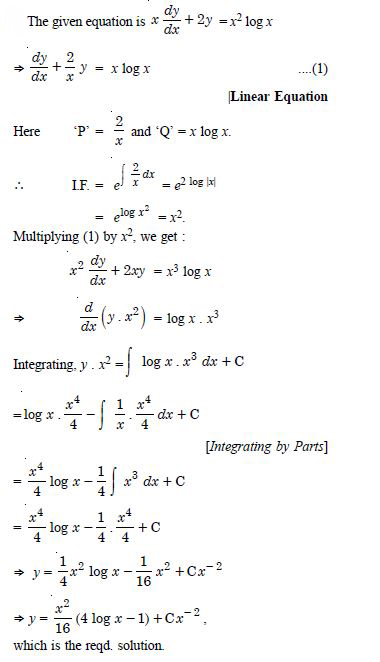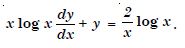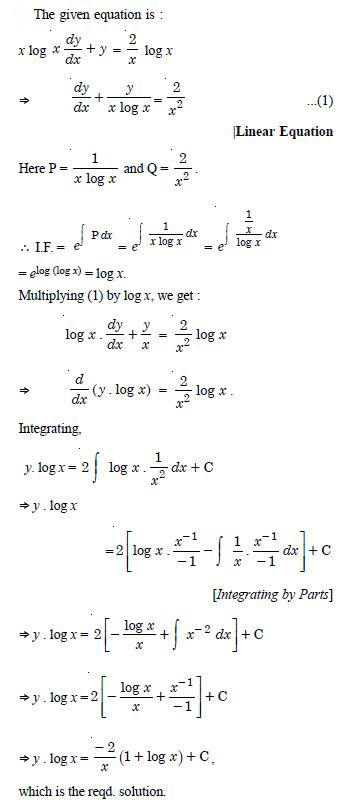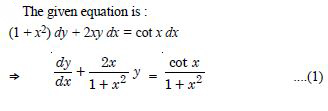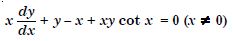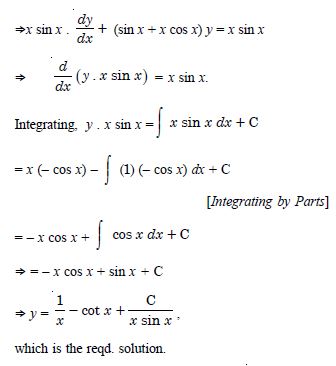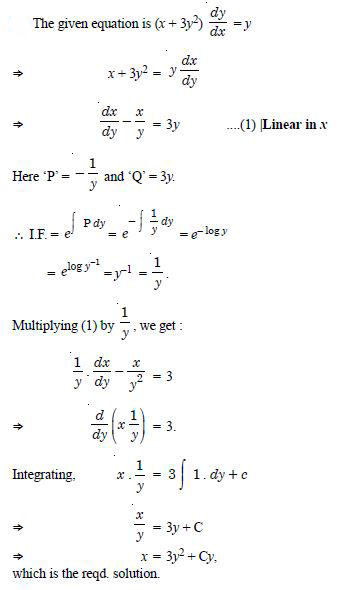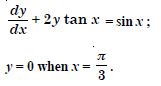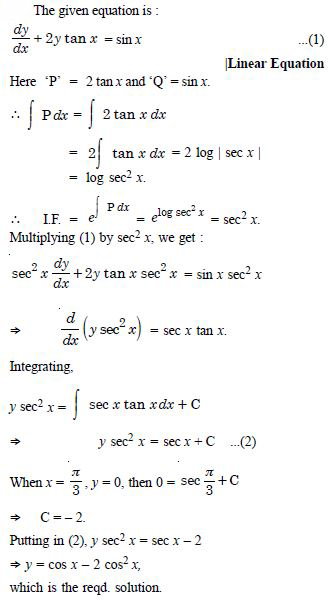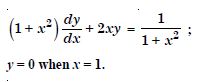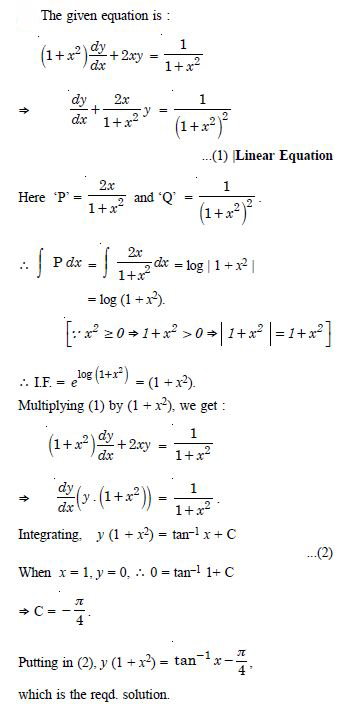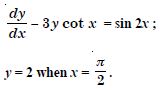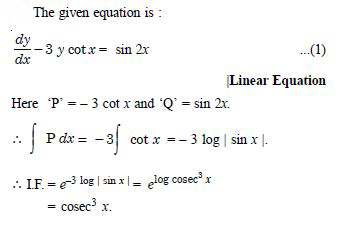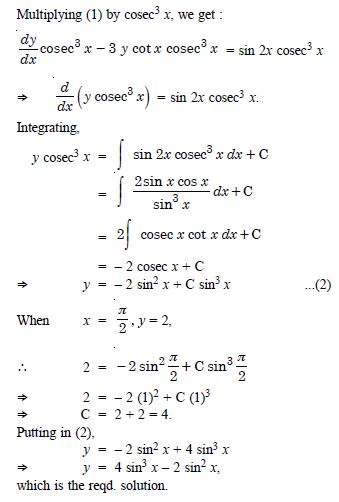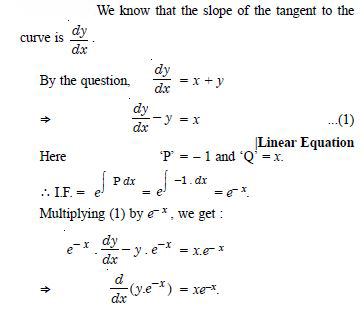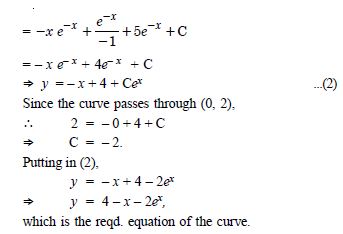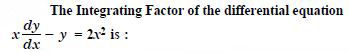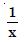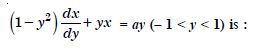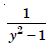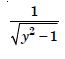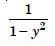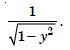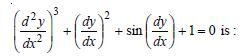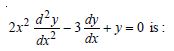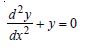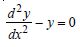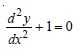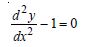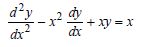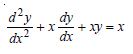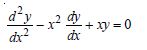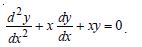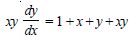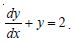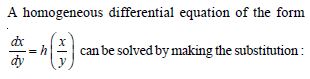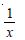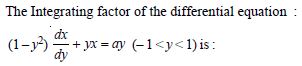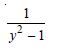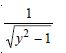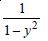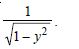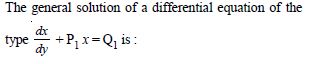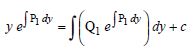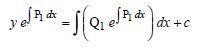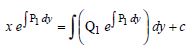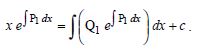NCERT Solutions for Class 12 Mathemetics Chapter 9 - Differential Equations

Question 1:

Determine order and degree (if defined) of differential equations given in

Question 2:

Determine order and degree (if defined) of differential equations given in y' + 5y = 0.

Question 3:

Determine order and degree (if defined) of differential equations given in

Question 4:

Determine order and degree (if defined) of differential equations given in

Question 5:

Determine order and degree (if defined) of differential equations given in

Question 6:

Determine order and degree (if defined) of differential equations given in
(y''')² + (y'')³ + (y')⁴ + y⁵ = 0.

Question 7:

Determine order and degree (if defined) of differential equations given in
y''' + 2y'' + y' = 0.

Question 8:

Determine order and degree (if defined) of differential equations given in
y'+ y = 0.

Question 9:

Determine order and degree (if defined) of differential equations given in
y''+ (y')² + 2y = 0.

Question 10:

Determine order and degree (if defined) of differential equations given in
y''+ 2y'+ sin y = 0.

Question 11:

The degree of the differential equation :

1. 3
2. 2
3. 1
4. not defined

Question 12:

The order of the differential equation :

1. 2
2. 1
3. 0
4. Not defined.

Question 13:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :
y = e^x + 1 : y''– y'= 0

Question 14:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :
y = x² + 2x + C : y'– 2x – 2 = 0.

Question 15:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :
y = cos x + C : y' sin x = 0

Question 16:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :

Question 17:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :
y = Ax : xy'= y (x $\ne$ 0)

Question 18:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :

Question 19:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :

Question 20:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :
y – cos x = x : (y sin y + cos y + x)y'= y.

Question 21:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :
x + y = tan^–1 y : y²y'+ y² + 1 = 0

Question 22:

Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation :

Question 23:

The number of arbitrary constants in the general solution of a differential equation of fourth order is :

1. 0
2. 2
3. 3
4. 4

Question 24:

The number of arbitrary constants in the particular solution of a differential equation of third order is :

1. 3
2. 2
3. 1
4. 0

Question 25:

Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b :

Question 26:

Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b :
y² = a (b² – x²)

Question 27:

Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b :
y = ae^3x + be^–2x

Question 28:

Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b :
y = e2x (a + bx)

Question 29:

Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b :
y = e^x (a cos x + b sin x).

Question 30:

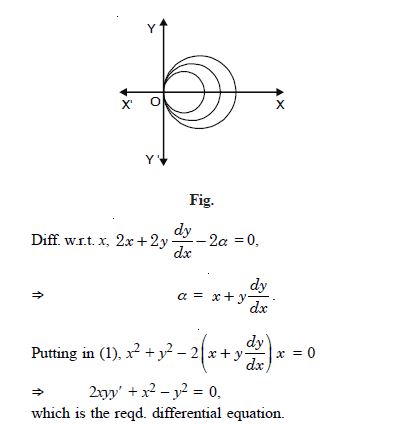
Form the differential equation of the family of circles touching the y-axis at origin.

Question 31:

Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.

Question 32:

Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.

Question 33:

Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.

Question 34:

Form the differential equation of the family of circles having centre on y-axis and radius 3 units.

Question 35:

Which of the following differential equation has y = C₁ e^x + C₂ e^–x as the general solution ?

Question 36:

Which of the following differential equations has y = x as one of its particular solution ?

Question 37:

For each of the differential equations, find the general solution :

Question 38:

For each of the differential equations, find the general solution :

Question 39:

For each of the differential equations, find the general solution :

Question 40:

For each of the differential equations, find the general solution :
sec² x tan y dx + sec² y tan x dy = 0.

Question 41:

For each of the differential equations, find the general solution :
(e^x + e^{– x}) dy – (e^x – e^{– x}) dx = 0.

Question 42:

For each of the differential equations, find the general solution :

Question 43:

For each of the differential equations, find the general solution :
y log y dx – x dy = 0.

Question 44:

For each of the differential equations, find the general solution :

Question 45:

For each of the differential equations, find the general solution :

Question 46:

For each of the differential equations, find the general solution :
e^x tan y dx + (1 – e^x) sec² y dy = 0.

Question 47:

For each of the differential equations find a particular solution satisfying the given condition :

Question 48:

For each of the differential equations find a particular solution satisfying the given condition :

Question 49:

For each of the differential equations find a particular solution satisfying the given condition :

Question 50:

For each of the differential equations find a particular solution satisfying the given condition :

Question 51:

Find the equation of a curve passing through the point (0, 0) and whose differential equation is :
y' = e^x sin x.

Question 52:

Question 53:

Find the equation of a curve passing through the point (0, – 2), given that at any point (x, y) on the curve the product of the slope of its tangent and y – co-ordinate of the point is equal to the x-co-ordinate of the point.

Question 54:

At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line joining the point of contact to the point (– 4, – 3). Find the equation of the curve, given that it passes through (– 2, 1).

Question 55:

The volume of a spherical balloon is being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units, find the radius of the balloon after ‘t’ seconds.

Question 56:

In a bank, principal increases at the rate of r% per year. Find the value of ‘r’ if ₹ 100 double itself in10 years (log_e 2 = 0·6931).

Question 57:

In a bank, principal, increases continuously at the rate of 5% per year. An amount of ₹ 1000 is deposited with this bank, how much will it worth after 10 years. (e^0·5 = 1·648)

Question 58:

In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the culture reach 2,00,000, if the rate of growth of bacteria is proportional to the number present ?

Question 59:

1. e^x + e^–y = C
2. e^x + e^y = C
3. e^–x + e^y = C
4. e^–x + e^–y = C

Question 60:

Show that the given differential equation is homogeneous and solve each of them :
(x² + xy) dy = (x² + y²) dx.

Question 61:

Show that the given differential equation is homogeneous and solve each of them :

Question 62:

Show that the given differential equation is homogeneous and solve each of them :
(x – y) dy – (x + y) dx = 0

Question 63:

Show that the given differential equation is homogeneous and solve each of them :
(x² – y²) dx + 2xy dy = 0.

Question 64:

Show that the given differential equation is homogeneous and solve each of them :

Question 65:

Show that the given differential equation is homogeneous and solve each of them :

Question 66:

Show that the given differential equation is homogeneous and solve each of them :

Question 67:

Show that the given differential equation is homogeneous and solve each of them :

Question 68:

Show that the given differential equation is homogeneous and solve each of them :

Question 69:

Show that the given differential equation is homogeneous and solve each of them :

Question 70:

For each of the differential equations find the particular solution satisfying the given condition :
(x + y) dy + (x – y) dx = 0 ;
y = 1 when x = 1.

Question 71:

For each of the differential equations find the particular solution satisfying the given condition :
x² dy + (xy + y²) dx = 0 ;
y = 1 when x = 1.

Question 72:

For each of the differential equations find the particular solution satisfying the given condition :

Question 73:

For each of the differential equations find the particular solution satisfying the given condition :

Question 74:

For each of the differential equations find the particular solution satisfying the given condition :

Question 75:

1. y = vx
2. y = yx
3. x = vy
4. x = y

Question 76:

Which of the following is a homogeneous differential equation ?

1. (4x + 6y + 5) dy – (3xy + 2x + 4) dx
2. (xy) dx – (x³ + y³) dy = 0
3. (x³ + 2y²) dx + 2xy dy = 0
4. y2dx + (x² – xy – y²) dy = 0.

Question 77:

For each of the differential equations find the general solutions :

Question 78:

For each of the differential equations find the general solutions :

Question 79:

For each of the differential equations find the general solutions :

Question 80:

For each of the differential equations find the general solutions :

Question 81:

For each of the differential equations find the general solutions :

Question 82:

For each of the differential equations find the general solutions :

Question 83:

For each of the differential equations find the general solutions :

Question 84:

For each of the differential equations find the general solutions :
(1 + x²) dy + 2xy dx = cot x dx (x $\ne$ 0).

Question 85:

For each of the differential equations find the general solutions :

Question 86:

For each of the differential equations find the general solutions :

Question 87:

For each of the differential equations find the general solutions :
y dx + (x – y²) dy = 0.

Question 88:

For each of the differential equations find the general solutions :

Question 89:

For each of the differential equations find a particular solution satisfying the given conditions :

Question 90:

For each of the differential equations find a particular solution satisfying the given conditions :

Question 91:

For each of the differential equations find a particular solution satisfying the given conditions :

Question 92:

Find the equation of a curve passing through the origin, given that the slope of the tangent to the curve at any point (x, y) is the equal to the sum of the co-ordinates of the point.

Question 93:

Find the equation of a curve passing through the point (0, 2), given that the sum of the co-ordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.

Question 94:

1. e^–x
2. e^–y

3. 

4. x

Question 95:

The Integrating Factor of the differential equation :

Question 96:

The degree of the differential equation :

1. 3
2. 2
3. 1
4. not defined

Question 97:

The order of the differential equation :

1. 2
2. 1
3. 0
4. not defined

Question 98:

The number of arbitrary constants in the general solution of a differential equation of fourth order is ;

1. 0
2. 2
3. 3
4. 4

Question 99:

The number of arbitrary constants in the particular solution of a differential equation of third order is :

1. 3
2. 2
3. 1
4. 0

Question 100:

Which of the following differential equations has y = c^{1 ex + c2 e–x as the general solution ?}

Question 101:

Which of the following differential equations has y = x as one of its particular solutions ?

Question 102:

1. e^x + e^–y = c
2. e^x + e^y = c
3. e^–x + e^y = c
4. e^–x + e^–y = c

Question 103:

Which of the following differential equations cannot be solved, using variable separable method ?

1. 

2. (y² – 2xy) dx = (x² – 2xy) dy

3. 

4. 

Question 104:

1. y = vx
2. v = yx
3. x = vy
4. x = v.

Question 105:

Which of the following is a homogeneous differential equation ?

1. (4x + 6y + 5) dy – (3y + 2x + 4) dx = 0
2. xy dx – (x³ + y³) dy = 0
3. (x³ + 2y²) dx + 2xy dy = 0
4. y² dx + (x² – xy – y²) dy = 0.

Question 106:

1. e^–x
2. e^–y

3. 

4. x

Question 107:

Question 108:

1. xy = c
2. x = cy²
3. y = cx
4. y = cx²

Question 109:

Question 110:

The general solution of the differential equation ex dy + (y e^x + 2x) dx = 0 is :

1. x e^y + x² = c
2. x e^y + y² = c
3. y e^x + x² = c
4. y e^y + x² = c.

Question 111:

The degree of the differential equation representing the family of curves (x – a)² + y² = 16 is :

1. 0
2. 2
3. 3
4. 1