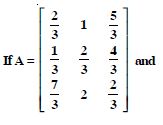
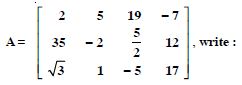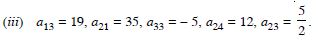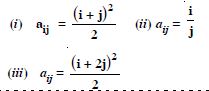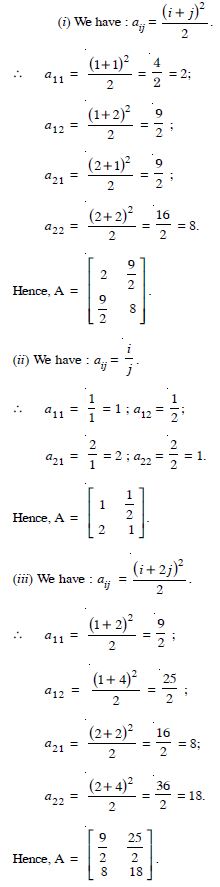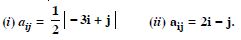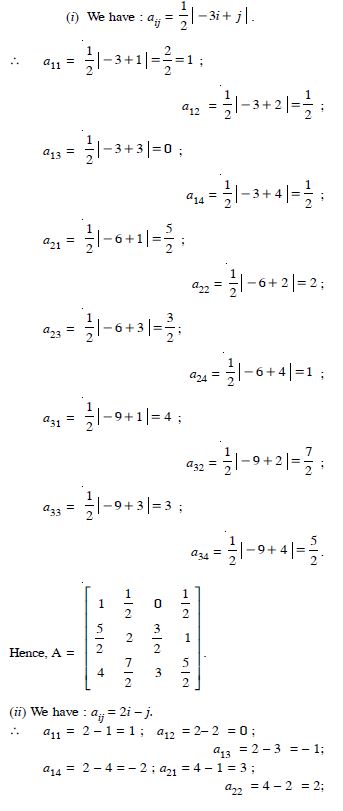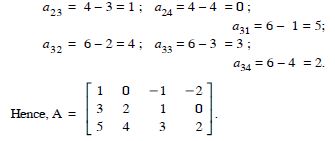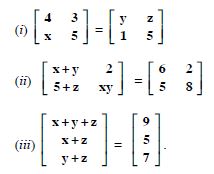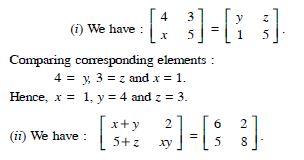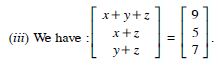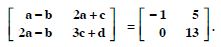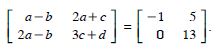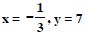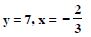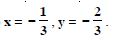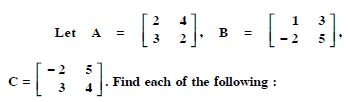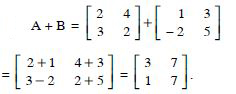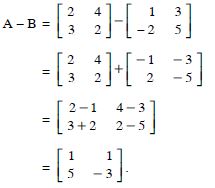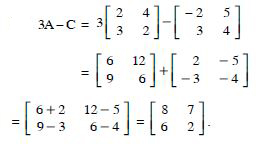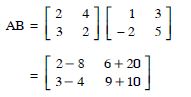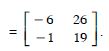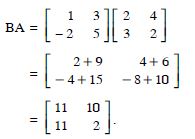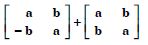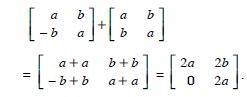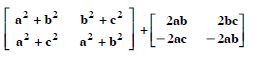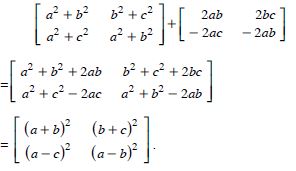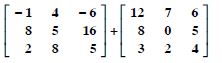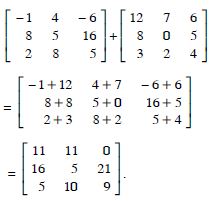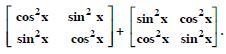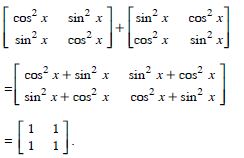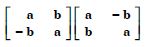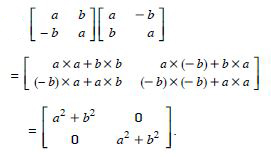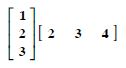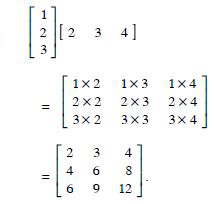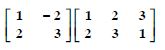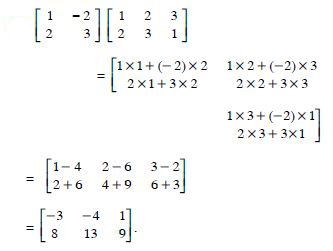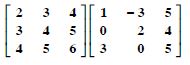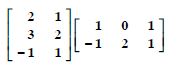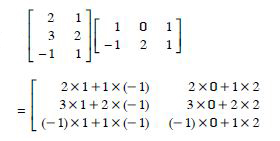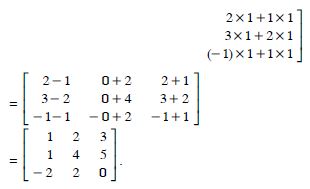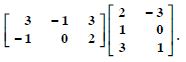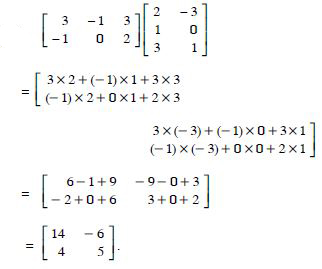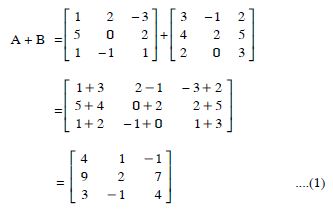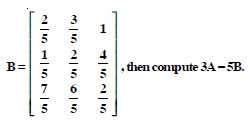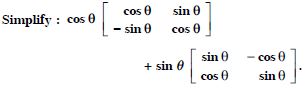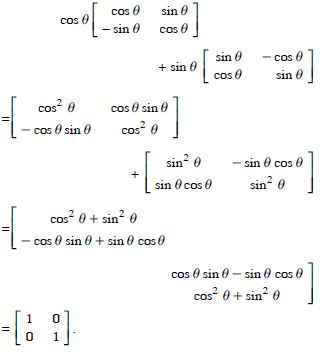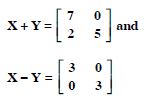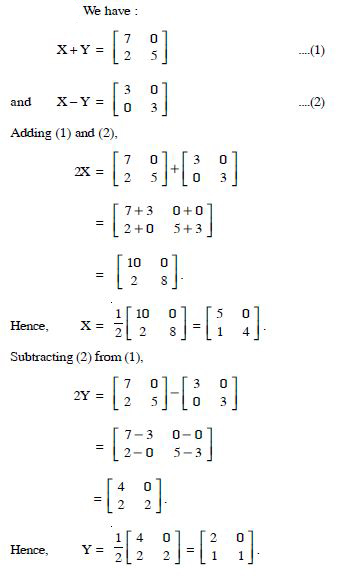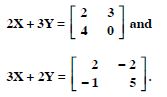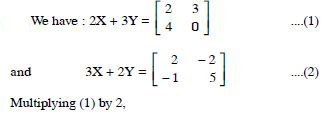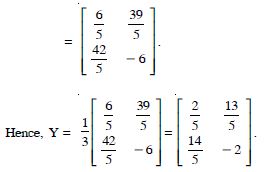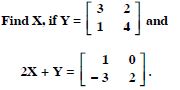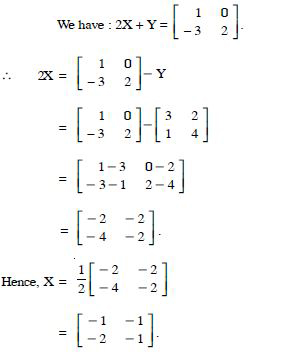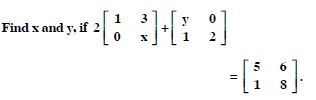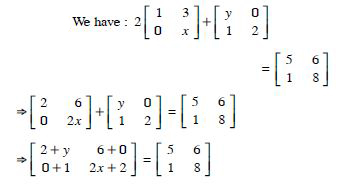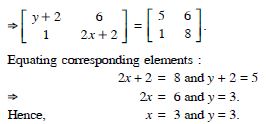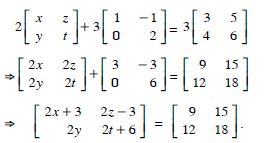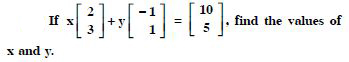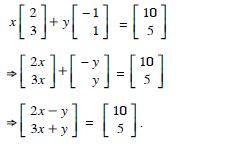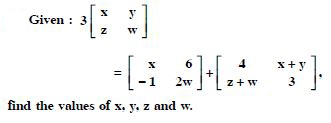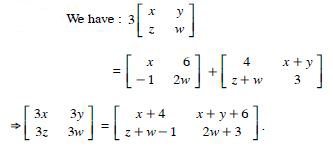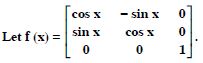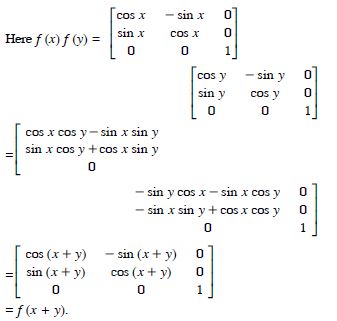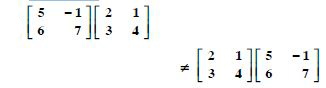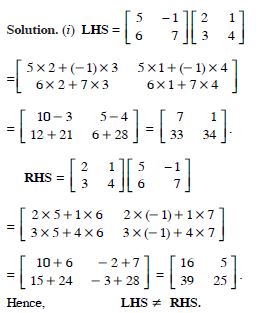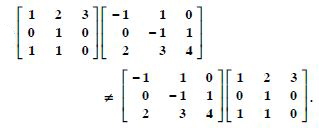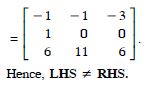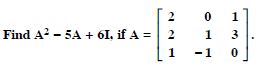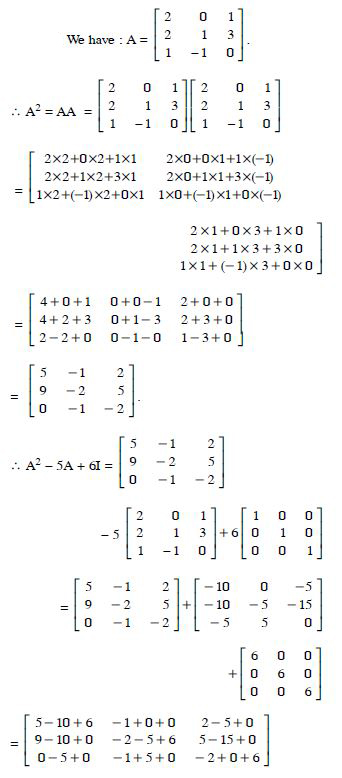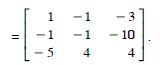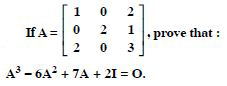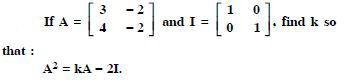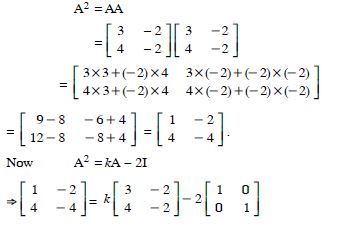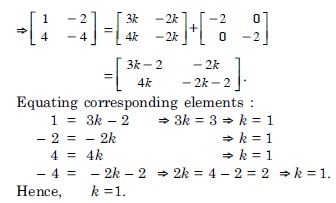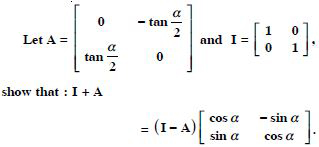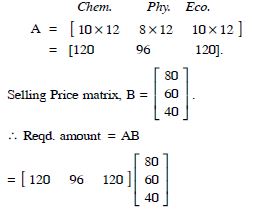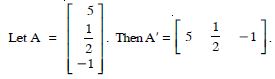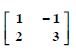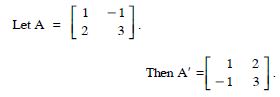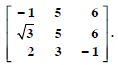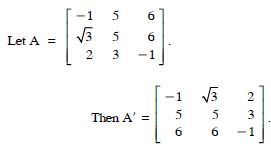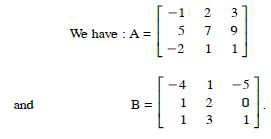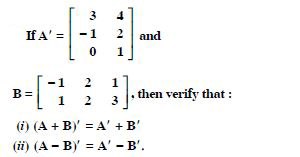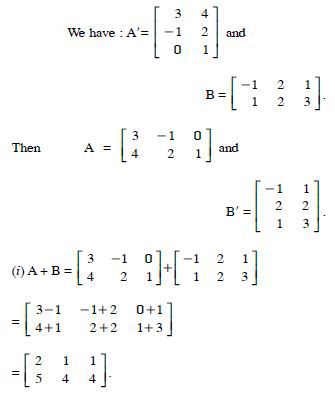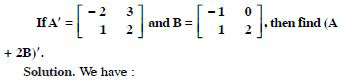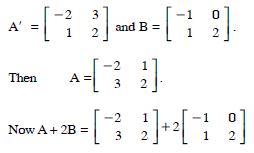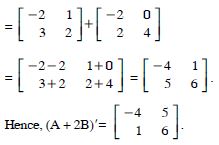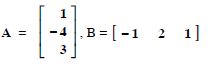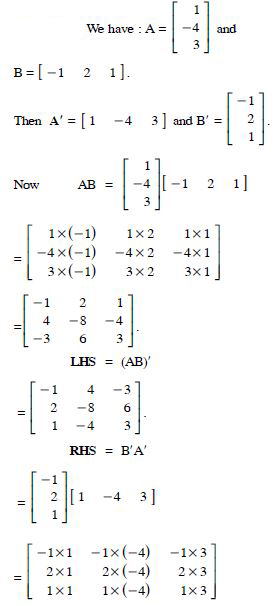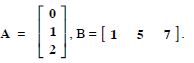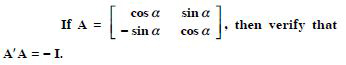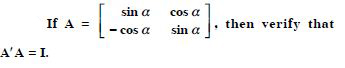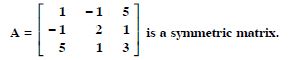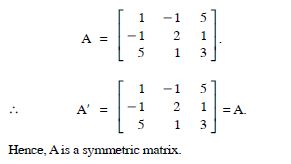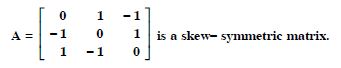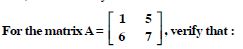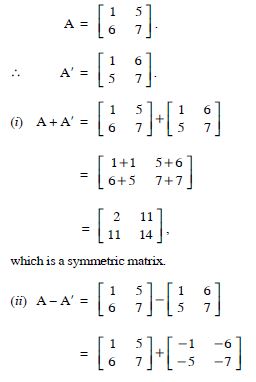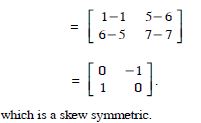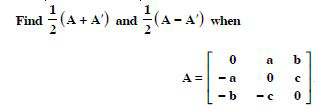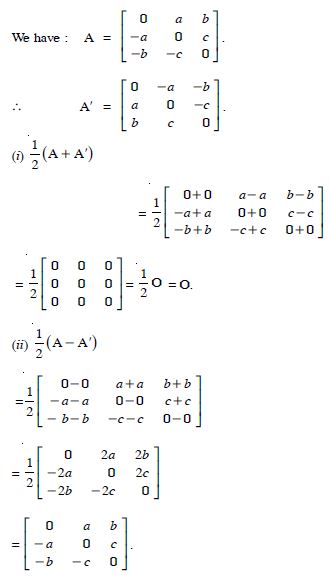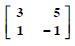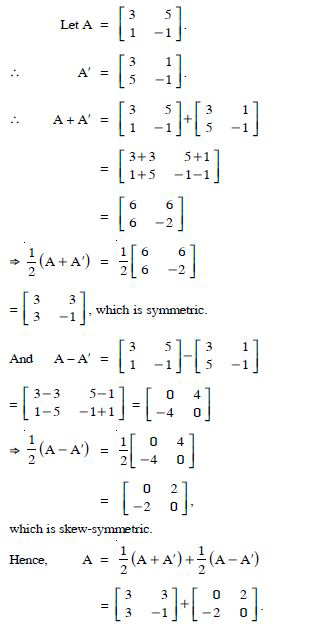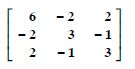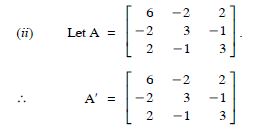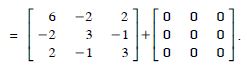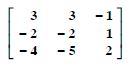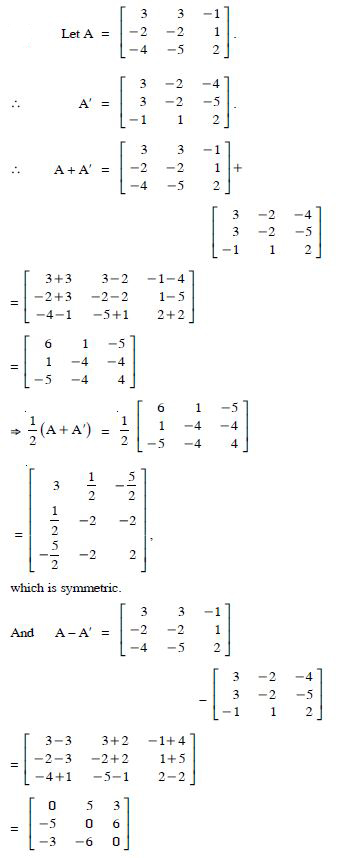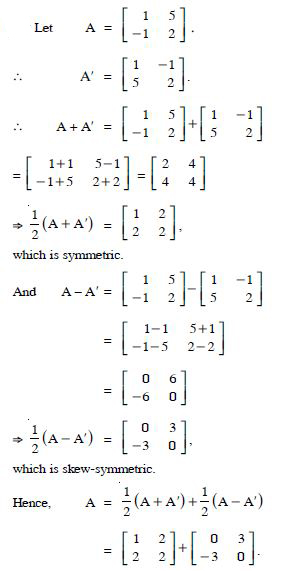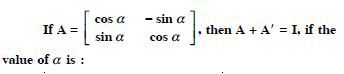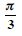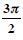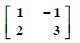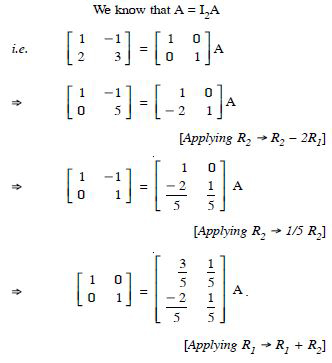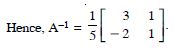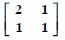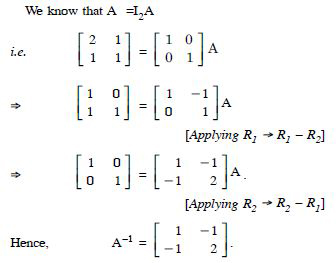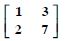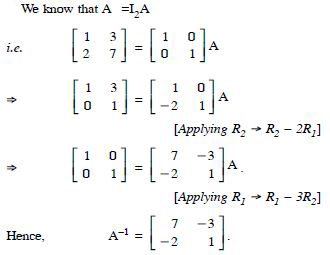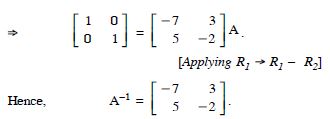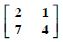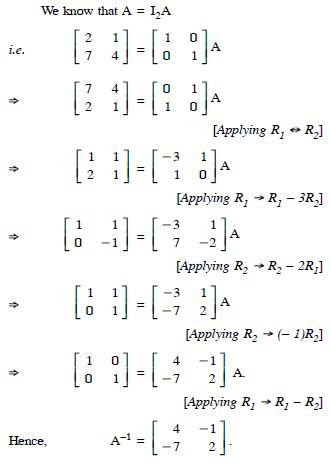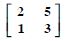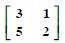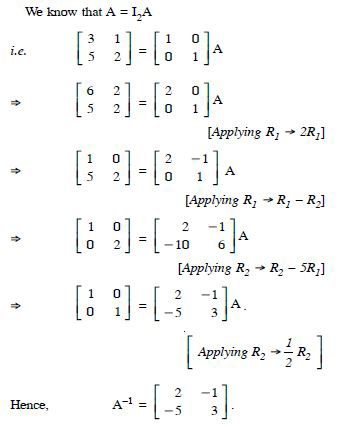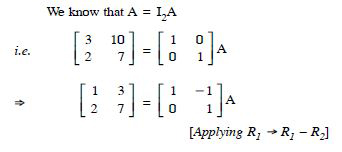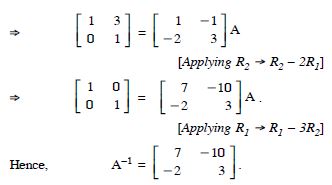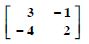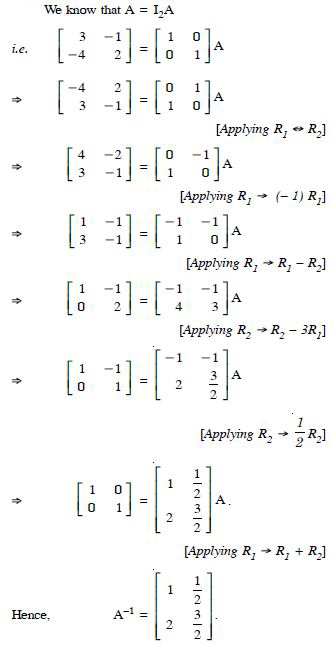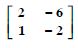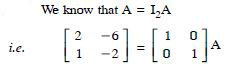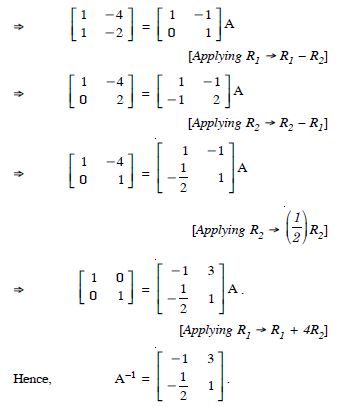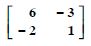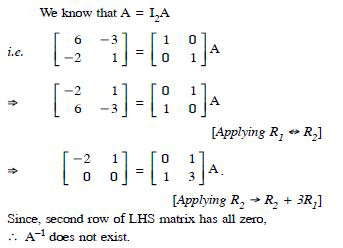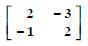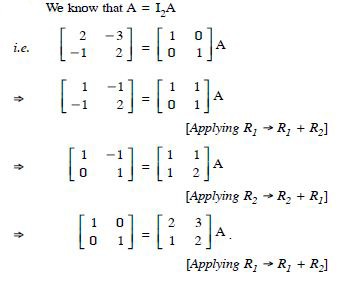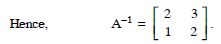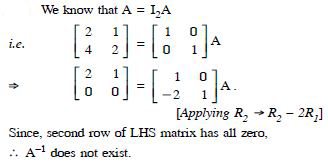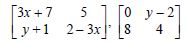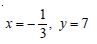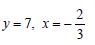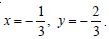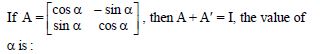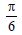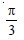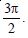Question 1:
In the matrix
(i) The order of the matrix.
(ii) The number of elements.
(iii) Write the elements a13, a21, a33, a24, a23.
Answer:
(i) The order of the matrix = 3 x 4.
(ii) The number elements = 3 x 4 = 12.
Question 2:
If a matrix has 24 elements, what are the possible orders it can have ? What, if it has 13 elements ?
Answer:
(i) Since
24 = 1 x 24 = 2 x 12 = 3 x 8 = 4 x 6,
there are 8 matrices having 24 elements.
Their orders are 1 x 24, 24 x 1, 2 x 12, 12 x 2, 3 x 8, 8 x 3, 4 x 6, 6 x 4.
(ii) Since 13 = 1 x 13,
there are 2 matrices having 13 elements.
Their orders are 1 x 13 and 13 x 1.
Question 3:
If a matrix has 18 elements, what are the possible orders it can have ? What, if it has 5 elements ?
Answer:
(i) Since 18 = 1 x 18 = 2 x 9 = 3 x 6,
there are 6 matrices having 18 elements.
Their oders are 1 x 18, 18 x 1, 2 x 9, 9 x 2, 3 x 6, 6 x 3.
(ii) Since 5 = 1 x 5,
there are 2 matrices having 5 elements.
Their orders are 1 x 5 and 5 x 1.
Question 4:
Construct a 2 x 2 matrix, A = [aij], whose elements are given by :
Answer:
Question 5:
Construct a 3 x 4 matrix whose elements are given by :
Answer:
Question 6:
Find the values of x, y and z from the following equations :
Answer:
Comparing corresponding elements :
x + y = 6 ...(1)
5 + z = 5 ...(2)
and xy = 8 ...(3)
From (1), y = 6 - x ...(4)
Putting in (3), x (6 - x) = 8
x2 - 6x + 8 = 0
(x - 2) (x - 4) = 0
x = 2, 4.
From (4), y = 6 - 2 = 4, 6 - 4 = 2.
Also from (2), z =0.
Hence, x = 2, y = 4, z = 0
or x = 4, y = 2, z = 0.
Comparing corresponding elements :
x + y + z = 9 ...(1)
x + z = 5 ...(2)
and y + z = 7 ...(3)
Subtracting (3) from (1),
x =2.
Subtracting (2) from (1),
y = 4.
Putting in (1), 2 + 4 + z = 9
z = 9 - 6 = 3.
Hence, x = 2, y = 4, and z = 3.
Question 7:
Find the values of a, b, c and d from the equation :
Answer:
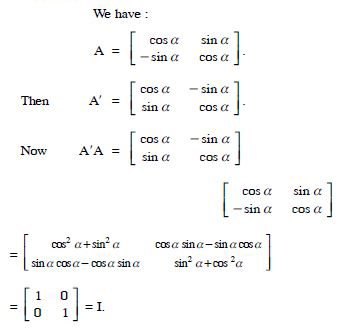
We have :
Comparing corresponding elements :
a - b = - 1 ...(1)
2a + c = 5 ...(2)
2a - b = 0 ...(3)
and 3c + d = 13 ...(4)
Subtracting (1) from (3),
a =1.
Putting in (3), 2(1) - b =0
b =2.
Putting in (2),2 (1) + c =5
c = 5 - 2 = 3.
Putting in (4),3 (3) + d =13
d = 13 - 9 = 4.
Hence, a = 1, b = 2, c = 3 and d = 4.
Question 8:
A = [aij]m x n is a square matrix, if :
- m < n
- m > n
- m = n
- None of these
Answer:
m = n
Question 9:
Which of the given values of x and y make the following pair of matrices equal ?
- Not possible to find
Answer:
Not possible to find
Reason : Comparing coresponding elements :
3x + 7 = 0 ...(1)
y - 2 = 5 ...(2)
y + 1 = 8 ...(3)
and 2 - 3x = 4 ...(4)
Thus x has two values.
Hence, it is not possible to find the values of x and y.
Question 10:
The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is :
- 27
- 18
- 81
- 512
Answer:
512
Question 11:
A + B
Answer:
Question 12:
A - B
Answer:
Question 13:
3A - C
Answer:
Question 14:
AB
Answer:
Question 15:
BA.
Answer:
Question 16:
Compute the following :
Answer:
Question 17:
Compute the following :
Answer:
Question 18:
Compute the following :
Answer:
Question 19:
Compute the following :
Answer:
Question 20:
Compute the indicated products :
Answer:
Question 21:
Compute the indicated products :
Answer:
Question 22:
Compute the indicated products :
Answer:
Question 23:
Compute the indicated products :
Answer:
Question 24:
Compute the indicated products :
Answer:
Question 25:
Compute the indicated products :
Answer:
Question 26:
Answer:
Question 27:
Answer:
Question 28:
Answer:
Question 29:
Find X and Y, if :
Answer:
Question 30:
Find X and Y, if :
Answer:
Question 31:
Answer:
Question 32:
Answer:
Question 33:
Solve the equation for x, y, z and t, if :
Answer:
We have :
Equating corresponding elements :
2x + 3 = 9 2x = 9 - 3 = 6 x = 3
2y = 12 y = 6
2z - 3 = 15 2z = 3 + 15 = 18 z = 9
and 2t + 6 = 18 2t = 18 - 6 = 12 t = 6.
Hence, x = 3, y = 6, z = 9 and t = 6.
Question 34:
Answer:
We have :
Equating corresponding elements :
2x - y = 10 ....(1)
and 3x + y = 5 ....(2)
Adding (1) and (2), 5x = 15 x = 3.
Putting in (1), 2 (3) - y = 10 y = 6 - 10 = - 4.
Hence, x = 3 and y = - 4.
Question 35:
Answer:
Equating corresponding elements :
3x = x + 4 2x = 4 x = 2
3y = x + y + 6 2y = 2 + 6 2y = 8 y = 4
3w =2w + 3 w = 3
and 3z = z + w - 1 2z = 3 - 1 = 2 z = 1.
Hence, x = 2, y = 4, z = 1 and w = 3.
Question 36:
Show that f (x) f (y) = f (x + y).
Answer:
Question 37:
Show that :
Answer:
Question 38:
Show that :
Answer:
Question 39:
Answer:
Question 40:
Answer:
Question 41:
Answer:
Question 42:
Answer:
Question 43:
A trust fund has ₹30,000 that must be invested in two different types of bonds. The first bond pays 5% and second 7% interest per year. Using matrix multiplication, determine how to divide ₹30,000 among the two types of bonds if the trust fund must obtain an annual total interest of :
(a) ₹1800 (b) ₹2000.
Answer:
Let ₹30,000 be divided into two parts :
₹ x invested in 1st type and ₹(30,000 - x) in 2nd type.
The values of the bonds are represented by 1 x 2 row matrix as :
A = [ x 30,000 − x ] .
The amount received as interest per ₹ annually are represented by 2 x 1 column matrix as :
Question 44:
The book shop of a particular school has 10 dozen Chemistry books, 8 dozen Physics books, 10 dozen Economics books. The selling prices are ₹80, ₹60 and ₹40 each respectively. Find the total amount, the book-shop will receive from selling all the books, using matrix algebra.
Answer:
Inventory,
= [9600 + 5760 + 4800] = [20160].
Hence, the book-shop will receive ₹ 20,160 by selling all the books.
Assume X, Y, Z, W and P are matrices of order 2 x n, 3 x k, 2 x p, n x 3 and p x k respectively. Choose the correct answer in (21 - 22) :
Question 45:
The restriction on n, k and p so that PY + WY will be defined as :
- k = 3, p = n
- k is arbitrary, p = 2
- p is arbitrary, k = 3
- k = 2, p = 3.
Answer:
k = 3, p = n
Question 46:
If n = p, then the order of 7X - 5Z is :
- p x 2
- 2 x n
- n x 3
- p x n.
Answer:
2 x n
Question 47:
Find the transpose of each of the following matrices :
Answer:
Question 48:
Find the transpose of each of the following matrices :
Answer:
Question 49:
Find the transpose of each of the following matrices :
Answer:
Question 50:
Answer:
Question 51:
Answer:
Question 52:
Answer:
We have :
Question 53:
For the matrices A and B, verify that :
(AB)′ = B′A′, where :
Answer:
Question 54:
For the matrices A and B, verify that :
(AB)′ = B′A′, where :
Answer:
Question 55:
Answer:
Question 56:
Answer:
Question 57:
Show that the matrix
Answer:
We have :
Question 58:
Show that the matrix
Answer:
We have :
Question 59:
(i) A + A′ is a symmetric matrix
(ii) A - A′ is a skew-symmetric matrix.
Answer:
We have :
Question 60:
Answer:
Question 61:
Express the following matrices as the sum of a symmetric and a skew-symmetric matrix :
Answer:
Question 62:
Express the following matrices as the sum of a symmetric and a skew-symmetric matrix :
Answer:
Question 63:
Express the following matrices as the sum of a symmetric and a skew-symmetric matrix :
Answer:
Question 64:
Express the following matrices as the sum of a symmetric and a skew-symmetric matrix :
Answer:
Question 65:
Choose the correct answer
If A, B are symmetric matrices of same order, then AB - BA is a :
- Skew-symmetric matrix
- Symmetric matrix
- Zero matrix
- Identity matrix
Answer:
Skew-symmetric matrix
Question 66:
Choose the correct answer
- π
Answer:
Question 67:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 68:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 69:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 70:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 71:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 72:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 73:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 74:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 75:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 76:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 77:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 78:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 79:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 80:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 81:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 82:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 83:
Using elementary transformations, find the inverse of each of the matrices, if it exists in
Answer:
Question 84:
Matrix A and B will be inverse of each other if
- AB = BA
- AB = BA = O
- AB = O, BA = I
- AB = BA = I.
Answer:
AB = BA = I.
Question 85:
If A = [aij]m x n is a square matrix, if :
- m < n
- m > n
- m = n
- None of these.
Answer:
m = n
Question 86:
Which of the given values of x and y make the following pair of matrices equal :
- Not possible to find
Answer:
Not possible to find
Question 87:
The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is :
- 27
- 18
- 81
- 512
Answer:
512
Question 88:
Assume X, Y, Z, W and P are matrices of order 2 x n, 3 x k, 2 x p, n x 3 and p x k respectively. Now answer the following
The restrictions on n, k and p so that PY + WY will be defined are :
- k = 3, p = n
- k is arbitrary, p = 2
- p is arbitrary
- k = 2, p = 3
Answer:
k = 3, p = n
Question 89:
Assume X, Y, Z, W and P are matrices of order 2 x n, 3 x k, 2 x p, n x 3 and p x k respectively. Now answer the following
If n = p, then the order of the matrix 7X - 5Z is :
- p x 2
- 2 x n
- n x 3
- p x n
Answer:
2 x n
Question 90:
If A, B are symmetric matrices of same order, then AB - BA is a :
- Skew-symmetric matrix
- Symmetric matrix
- Zero matrix
- Identity matrix.
Answer:
Skew-symmetric matrix
Question 91:
Answer:
Question 92:
Matrices A and B will be inverse of each other only if :
- AB = BA
- AB - BA = O
- AB = O, BA = I
- AB = BA = I
Answer:
AB = BA = I
Question 93:
- 1 + 2 + = 0
- 1 - 2 + = 0
- 1 - 2 - = 0
- 1 + 2 - = 0
Answer:
1 - 2 - = 0
Question 94:
If a matrix is both symmetric and skew-symmetric matrix, then :
- A is a diagonal matrix
- A is a zero matrix
- A is a square matrix
- None of these.
Answer:
A is a zero matrix
Question 95:
If A is a square matrix such that A2 = A, then (I + A)3 - 7A is equal to :
- A
- I - A
- I
- 3A.
Answer:
I