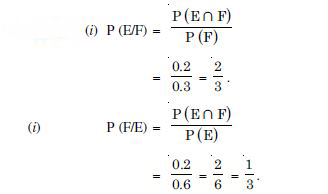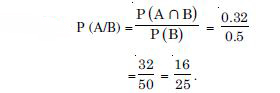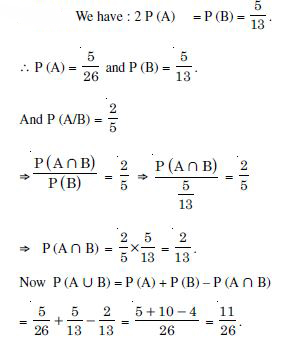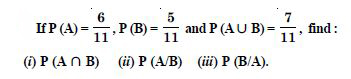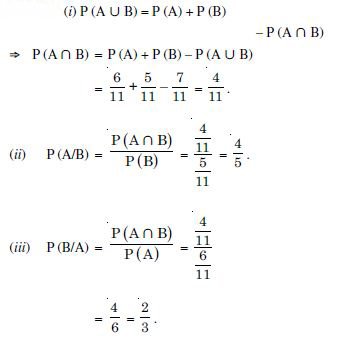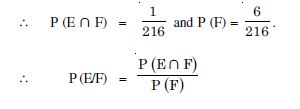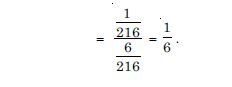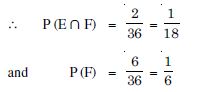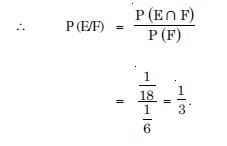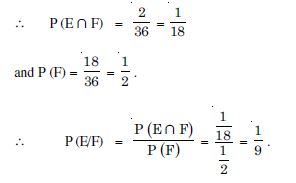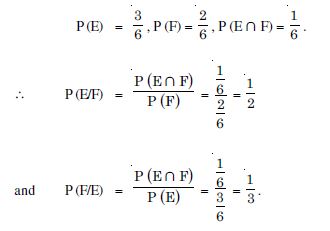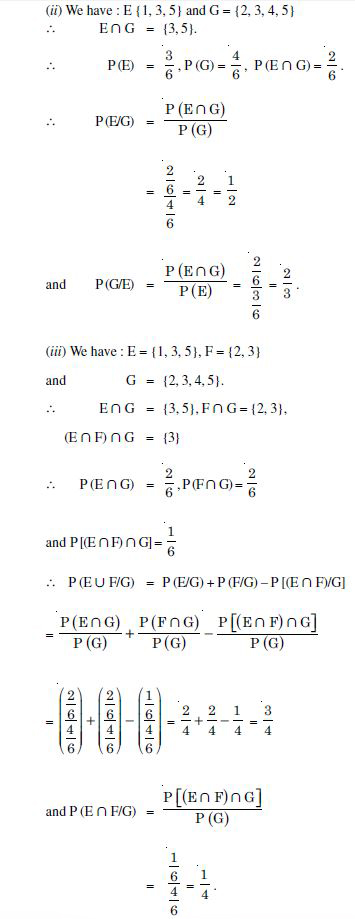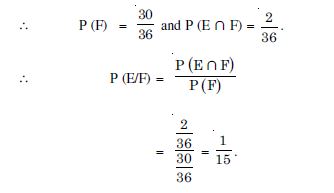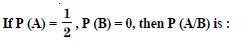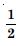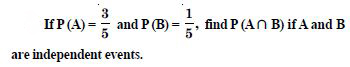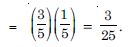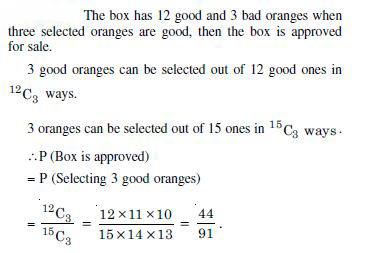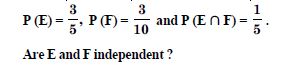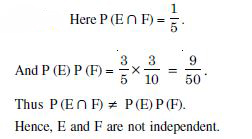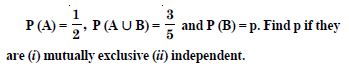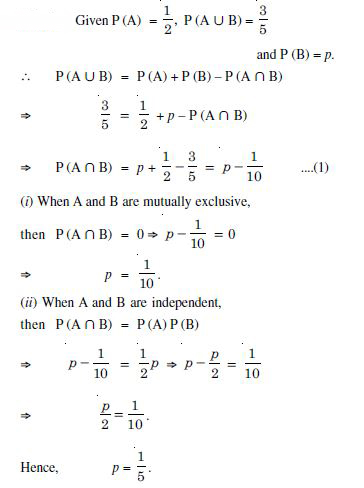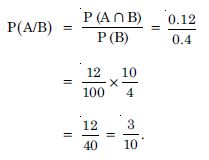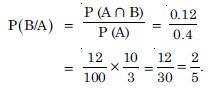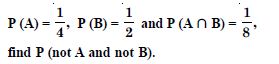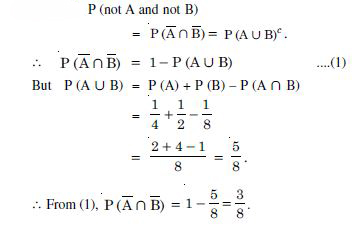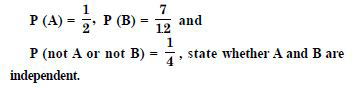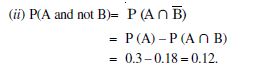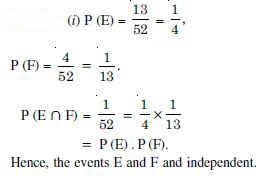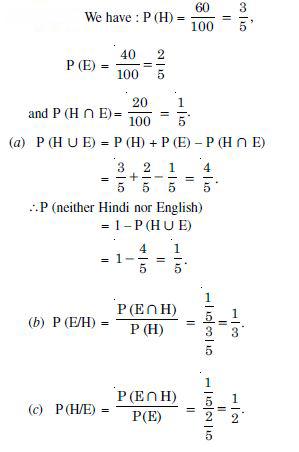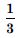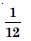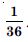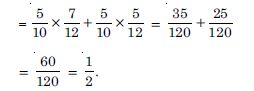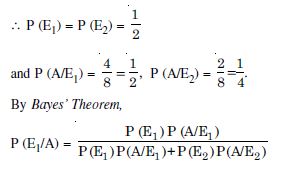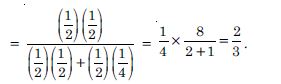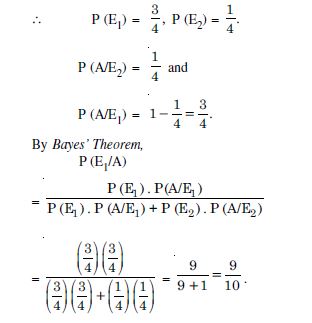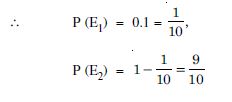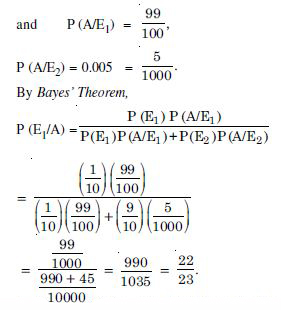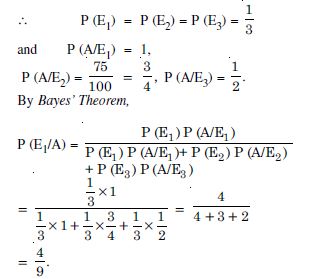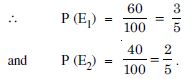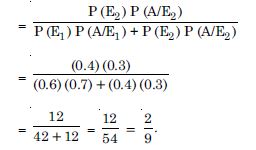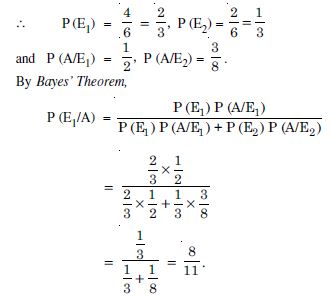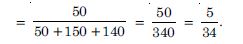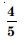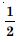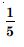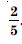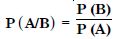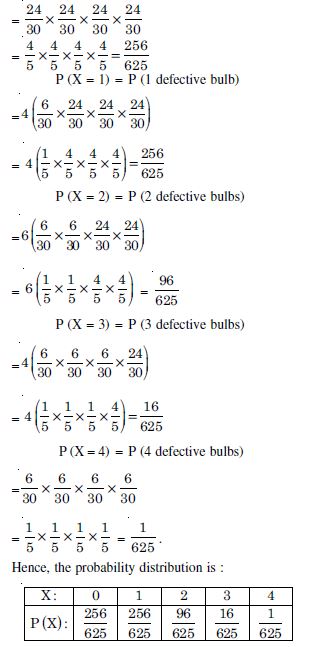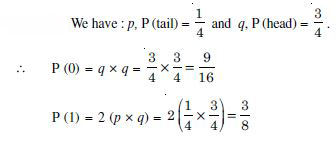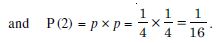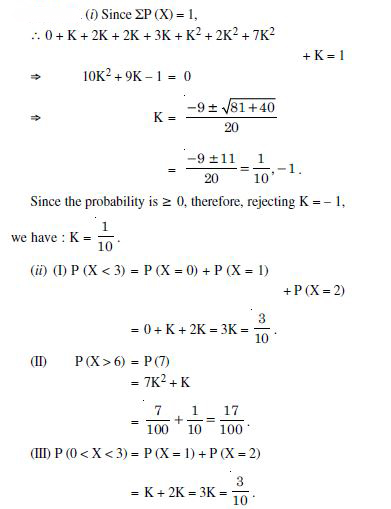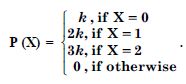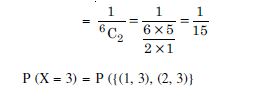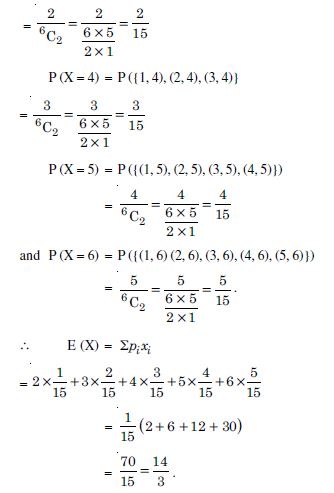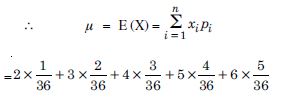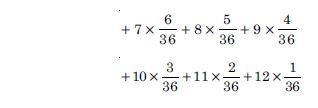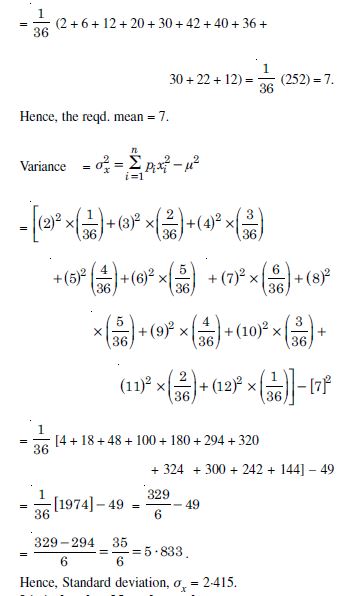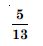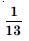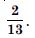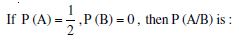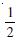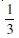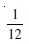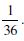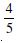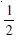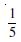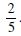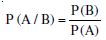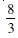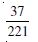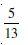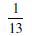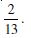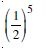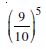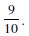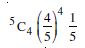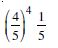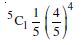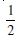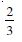NCERT Solutions for Class 12 Mathemetics Chapter 13 - Probability

Question 1:

Given that E and F are events such that :
P (E) = 0.6, P(F) = 0.3 and P (E ∩ F) = 0.2 find P (E/F) and P (F/E).

Question 2:

Compute P (A/B), if P (B) = 0.5 and P (A $\cap$ B) = 0.32.

Question 3:

If P (A) = 0.8, P (B) = 0.5 and P (B/A) = 0.4, find
(i) P (A ∩ B) (ii) P (A/B) (iii) P (A $\cup$ B).

Question 4:

Question 5:

Question 6:

A coin is tossed three times, where :
(i) E : head on third toss ; F : heads on first two tosses
(ii) E : at least two heads ; F : at most two heads
(iii) E : at most two tails ; F : at least one tail.

Question 7:

Two coins are tossed once, where :
(i) E : tail appears on one coin ;
F : one coin shows head
(ii) E : no tail appears ; F : no head appears.

Question 8:

A die is thrown three times.
E : 4 appears on the third toss
F : 6 and 5 appear respectively on first two tosses.

Question 9:

Mother, father and son line up at random for a family picture :
E : son on one end ; F : father in middle.

Question 10:

A black and a red dice are rolled.
Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.

Question 11:

A black and a red dice are rolled.
Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.

Question 12:

A fair die is rolled. Consider E = {1, 3, 5}.
F = {2, 3} and G = {2, 3, 4, 5}. Find :
(i) P (E/F) and P (F/E) (ii) P (E/G) and P (G/E)
(iii) P ((E $\cup$ F)/G) and P ((E ∩ F)/G).

Question 13:

Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the probability that both are girls given that (i) the youngest is a girl (ii) at least one is a girl ?

Question 14:

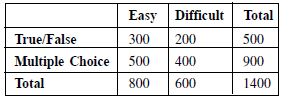
An instructor has a question bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question, given that it is a multiple choice question ?

Question 15:

Given that the two numbers appearing on throwing two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.

Question 16:

Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least the die shows 3’.

Question 17:

1. 0
2. choose the correct answer :
   

   

3. not defined
4. 1

Question 18:

If A and B are events such that
P (A/B) = P (B/A), then :

1. A $\subset$ B but A $\ne$ B
2. A = B
3. A $\cap$ B = $\mathrm{\varphi }$
4. P (A) = P (B).

Question 19:

Question 20:

Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.

Question 21:

A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.

Question 22:

A fair coin and an unbiased die are tossed. Let A be the event ‘head appears on the coin’’ and B be the event ‘3 on the die’. Check whether A and B are independent or not.

Question 23:

A die marked 1, 2, 3, in red and 4, 5, 6 in green is tossed. Let A be the event, ‘the number is even’ and B be the event ‘the number is red’. Are A and B independent ?

Question 24:

Let E and F be events with :

Question 25:

Given that the events A and B are such that :

Question 26:

Let A and B be independent events with P (A) = 0.3 and P (B) = 0.4. Find :
P (A $\cap$ B)

Question 27:

Let A and B be independent events with P (A) = 0.3 and P (B) = 0.4. Find :
P (A $\cup$ B)

Question 28:

Let A and B be independent events with P (A) = 0.3 and P (B) = 0.4. Find :
P (A/B)

Question 29:

Let A and B be independent events with P (A) = 0.3 and P (B) = 0.4. Find :
P (B/A).

Question 30:

If A and B are two events such that :

Question 31:

Events A and B are such that :

Question 32:

Given two independent events A and B such that
P (A) = 0.3, P (B) = 0.6.
Find : (i) P (A and B)
(ii) P (A and not B)
(iii) P (A or B)
(iv) P (neither A nor B).

Question 33:

A die is tossed thrice. Find the probability of getting an odd number at least once.

Question 34:

Two balls are drawn at random with replacement
from a box containing 10 black and 8 red balls. Find the probability that :
(i) both balls are red
(ii) first ball is black and second is red
(iii) one of them is black and other is red.

Question 35:

Question 36:

One card is drawn at random from a well shuffled
deck of 52 cards. In which of the following cases are the events E and F independent ?
(i) E : the card drawn is a spade’
F : ‘the card drawn is an ace’.
(ii) E : ‘the card drawn is black’
F : ‘the card drawn is a king’.
(iii) E : ‘the card drawn is a king or queen’
F : ‘the card drawn is a queen or jack’.

Question 37:

In a hostel 60% of the students read Hindi newspaper, 40% read English newspaper and 20%, read both Hindi and English newspapers. A student is selected at random.
(a) Find the probability that she reads neither Hindi nor English newspapers.
(b) If she reads Hindi newspaper, find the probability that she reads English newspaper.
(c) If she reads English newspaper, find the probability that she reads Hindi newspaper.

Question 38:

The probability of obtaining an even prime number on each die, when a pair of dice is rolled is :

1. 0

2. 

3. 

4. 

Question 39:

Choose the correct-answer
Two events A and B are said to be independent if :

1. A and B are mutually exclusive
2. P (A′B′) = [1 – P (A)] [1 – P (B)]
3. P (A) = P (B)
4. P (A) + P (B) = 1.

Question 40:

An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a red ball is drawn at random. What is the probability that the second ball is red ?

Question 41:

A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag, which is found to be red. Find the probability that the ball is drawn from the first bag.

Question 42:

Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of the students who reside in hostel attain A grade and 20% of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is a hostlier ?

Question 43:

Question 44:

A laboratory blood test is 99% effective in detecting a certain disease when it is in fact present. However, the test also yields a false positive result for 0.5% of the healthy person tested i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease. If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease, given that his test results in positive ?

Question 45:

There are three coins. One is a two-headed coin (having head on both sides), another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin ?

Question 46:

Question 47:

A factory has two machines A and B. Past record shows that machine A produced 60% of the items of output and machine B produced 40% of the items. Further, 2% of the items produced by machine A and 1% produced by machine B were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine B ?

Question 48:

Two groups are competing for the position on the Board of Directors of Corporation. The probability that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3, if the second group wins. Find the probability that the new product was introduced by the second group.

Question 49:

Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin once and notes whether a head or tail is obtained. If she attained exactly one head, what is the probability that she threw 1, 2, 3, or 4 with the die ?

Question 50:

A manufacturer has three machine operators A, B and C. The first operator A produces 1% defective items, whereas the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B is on the job for 30% of the time and C is on the job for 20% of the time. A defective item is produced, what is the probability that it was produced by A ?

Question 51:

A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.

Question 52:

Question 53:

If A and B are two events such that A ⊂ B and P (B) ≠ 0, then which of the following is correct ?

1. 

2. P (A/B) < P (A)
3. P (A/B) $\ge$ P (A)
4. None of these.

Question 54:

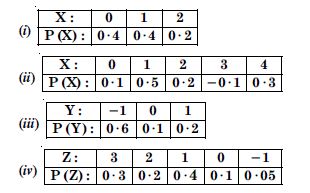
State which of the following are not the probability distribution of a random variable. Give reasons for your answer.

Question 55:

An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represent the number of black balls. What are the possible values of X? Is X a random variable ?

Question 56:

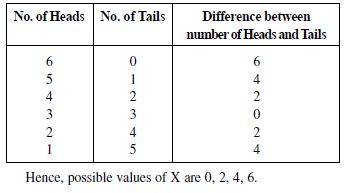
Let X represent the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are possible values of X ?

Question 57:

Find the probability distribution of :
Number of heads in two tosses of a coin.

Question 58:

Find the probability distribution of :
Number of tails in the simultaneous tosses of three coins.

Question 59:

Find the probability distribution of :
Number of heads in four tosses of a coin.

Question 60:

Find the probability distribution of the number of successes in two tosses of a die when a success is defined as (i) ‘a number greater than 4’ (ii) six appears on at least one die.

Question 61:

From a lot of 30 bulbs, which include 6 defective-bulbs, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.

Question 62:

A coin is biased so that the head is 3 times as likely to occur as a tail. If the coin is tossed twice, find the probability distribution for the number of tails.

Question 63:

A random variable X has the following probability distribution :

Question 64:

The random variable X has a probability distribution P (X) of the following form, where k is some number :

(a) Determine the value of k.
(b) Find P (X < 2), P (X $\le$ 2), P (X $\ge$ 2).

Question 65:

Find the mean number of heads in three tosses of a fair coin.

Question 66:

Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.

Question 67:

Two numbers are selected at random (without replacement) from first six positive integers. Let X denote the larger of the two numbers obtained. Find E (X).

Question 68:

Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.

Question 69:

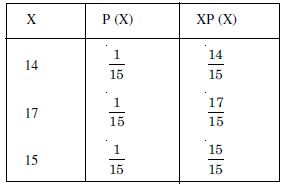
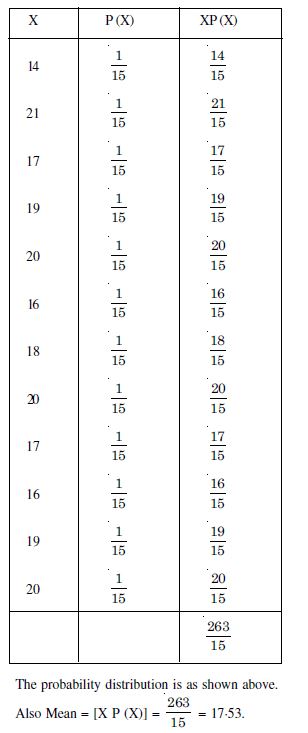
A class has 15 students whose ages are :
14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years.
One student is selected in such a manner that each has the same chance of having chosen and the age of X of the selected student is noted. What is the probability distribution of the random variable X ? Find the mean.

Question 70:

In a meeting 70% of the members favour a certain proposal, 30% having opposed. A member is selected at random and we let X = 0, if he opposed and X = 1, if he is in favour. Find E (X) and Var. (X).

Question 71:

The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is :

1. 1
2. 2
3. 5

4. 

Question 72:

Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E (X) is :

Question 73:

1. 0

2. 

3. not defined
4. 1

Question 74:

If A and B are events such that P (A/B) = P(B/A), then :

1. A $\subset$ B but A $\ne$ B
2. A = B
3. A $\cap$ B = $\mathrm{\varphi }$
4. P (A) = P (B)

Question 75:

The probability of obtaining an even prime number on each die when a pair of dice is rolled is :

1. 0

2. 

3. 

4. 

Question 76:

Two events A and B are said to be independent if :

1. A and B are mutually exclusive
2. P (A′B′) = [1 – P (A)] [1 – P (B)]
3. P (A) = P (B)
4. P (A) + P (B) = 1.

Question 77:

Question 78:

If A and B are two events such that A $\subset$ B and P (B) $\ne$ 0, then which of the following is correct :

1. 

2. P (A/B) < P (A)
3. P (A/B) $\ge$ P (A)
4. None of these.

Question 79:

If A and B are two events such that
P (A) $\ne$ 0 and P (B/A) = 1, then :

1. A $\subset$ B
2. B $\subset$ A
3. B = $\mathrm{\varphi }$
4. A = $\mathrm{\varphi }$.

Question 80:

If P (A/B) > P (A), then which of the following is correct?

1. P (B/A) < P (B)
2. P (A $\cap$ B) < P (A).P(B)
3. P (B/A) > P (B)
4. P (B/A) = P (B).

Question 81:

If A and B are any two events such that
P (A) + P (B) – P (A and B) = P (A), then :

1. P (B/A) = 1
2. P (A/B) = 1
3. P (B/A) = 0
4. P (A/B) = 0

Question 82:

The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is :

1. 1
2. 2
3. 5

4. 

Question 83:

Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. What is the value of E (X) ?

Question 84:

In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is :

1. 10^–1

2. 

3. 

4. 

Question 85:

1. 

2. 

3. 

4. None of these

Question 86:

A die is thrown once, then the probability of getting a number greater than 3 is :

1. 

2. 

3. 6
4. 0