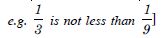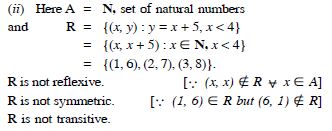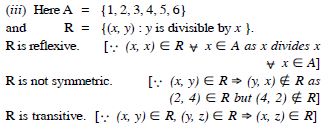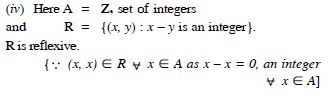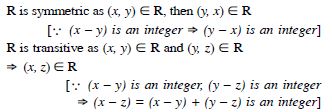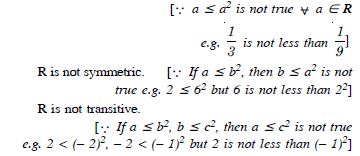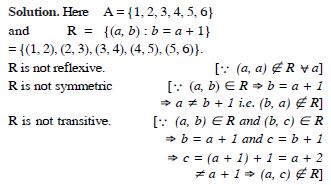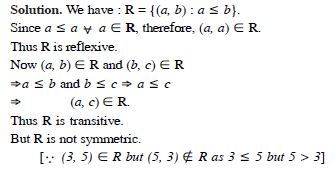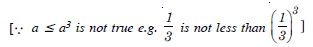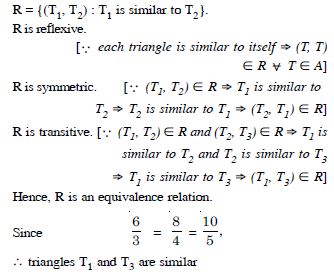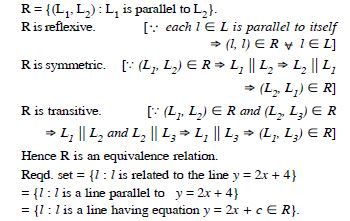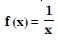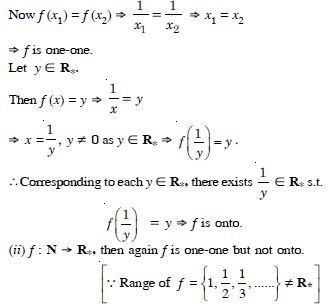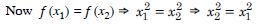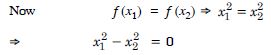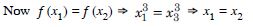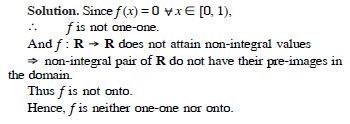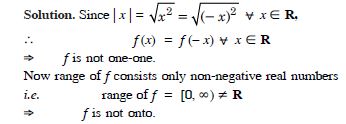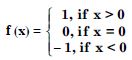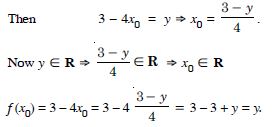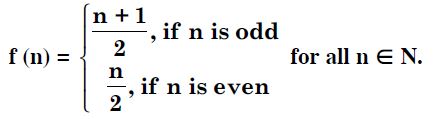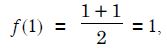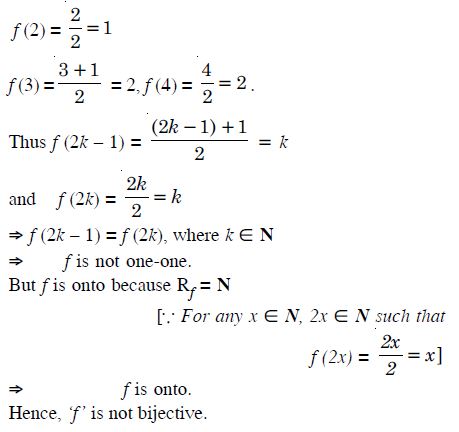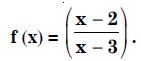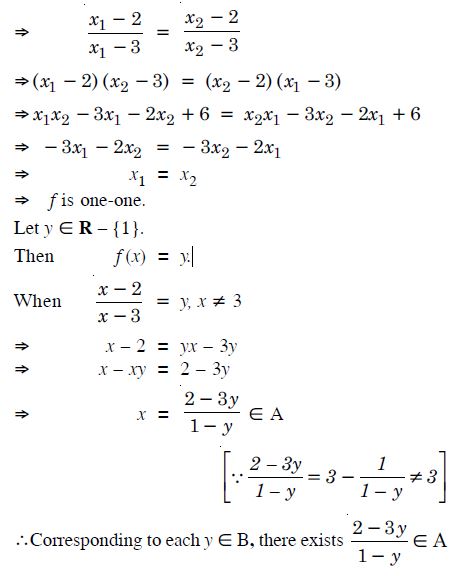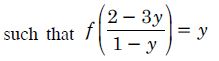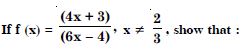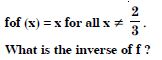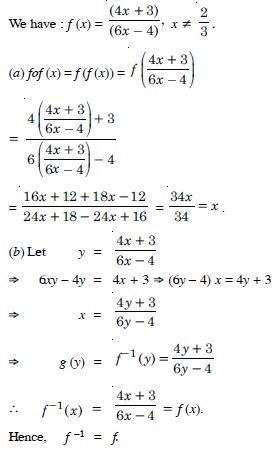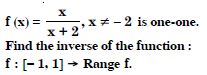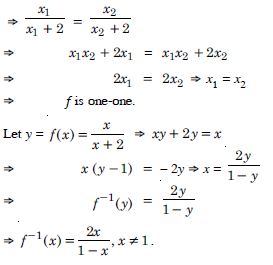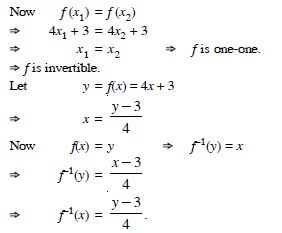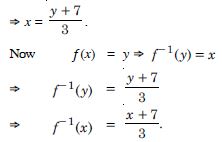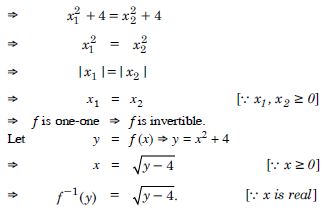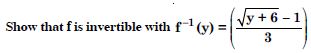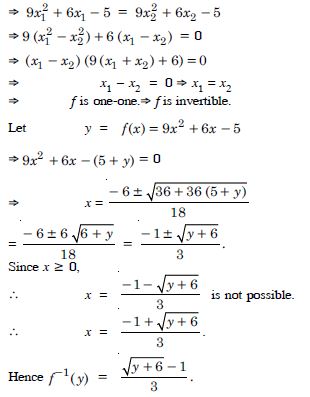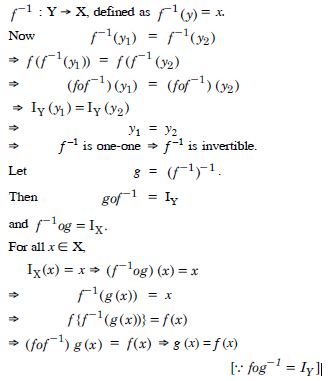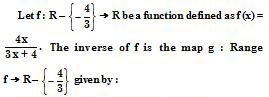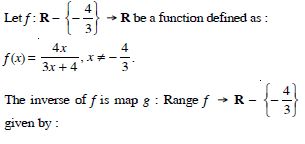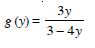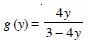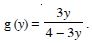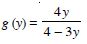NCERT Solutions for Class 12 Mathematics Relations and Functions

Question 1:

Determine whether each of the following relations are reflexive, symmetric and transitive : Relation R in the set A = {1, 2, 3, ......, 13, 14} defined as : R = {(x, y) : 3x – y = 0}

Answer:

Here
A = {1, 2, 3, ....... , 13, 14}
and R = {(x, y) : 3x – y = 0}

Show Answer

Question 2:

Determine whether each of the following relations are reflexive, symmetric and transitive :
Relation R in the set N of natural numbers defined as :
R = {(x, y) : y = x + 5 and x < 4}

Answer:

Show Answer

Question 3:

Determine whether each of the following relations are reflexive, symmetric and transitive :
Relation R in the set A = {1, 2, 3, 4, 5, 6} defined as :
R = {(x, y) : y is divisible by x }

Answer:

Show Answer

Question 4:

Determine whether each of the following relations are reflexive, symmetric and transitive :
Relation R in the set Z of all integers defined as :
R = {(x, y) : x – y is an integer}

Answer:

Show Answer

Question 5:

Determine whether each of the following relations are reflexive, symmetric and transitive :
Relation R in the set A of human beings in a town at a particular time given by :
(a) R = {(x, y) : x and y work at the same place}
(b) R = {(x, y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R = {(x, y) : x is wife of y}
(e) R = {(x, y) : x is father of y}.

Answer:

Show Answer

Question 6:

Show that the relation R in the set R of real numbers, defined as :
R = {(a, b) : a $\leq$ b²} is neither reflexive nor symmetric nor transitive.

Answer:

R is not reflexive.

Show Answer

Question 7:

Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as :
R = {(a, b) : b = a + 1}, is reflexive, symmetric or transitive.

Answer:

Show Answer

Question 8:

Show that the relation R in R defined as :
R = {(a, b) : a $\leq$ b}
is reflexive and transitive but not symmetric.

Answer:

Show Answer

Question 9:

Check whether the relation R in R defined by :
R = {(a, b) : a $\leq$ b³}
is reflexive, symmetric or transitive.

Answer:

R is not reflexive.

R is not symmetric.
[ $∴$ If a $\leq$ b³, then b is not less than or equal to a³
e.g. 1 $\leq$ 3³. But 3 is not less then 1³]
R is not transitive.
[ $∴$ If a $\leq$ b³ and b $\leq$ c³, then a is not necessarily less than or equal to c³
e.g. Take a = 7, b = 2, c = 1·5.
Here a < b³ as 7 < 2³ = 8
b < c³ as 2 < (1·5)³ = 3.375
But a > c³ as 7 > (1·5)³ = 3·375]

Show Answer

Question 10:

Show that the relation R in the set {1, 2, 3} defined as :
R = {(1, 2), (2, 1)}, is symmetric but neither reflexive nor transitive.

Answer:

Here R = {(1, 2), (2, 1)}.
R is not reflexive. [ $∴$ (1, 1), (2, 2), (3, 3) $\notin$ R]
R is not transitive.
[ $∴$ (1, 2) $\in$ R, (2, 1) $\in$ R but (1, 1) $\notin$ R]
R is symmetric. [ $∴$ (1, 2) $\in$ R and (2, 1) $\in$ R]

Show Answer

Question 11:

Show that the relation R in the set A of all books in a library of a college, given by :
R = {(x, y) : x and y have same number of pages} is an equivalence relation.

Answer:

We have :

Show Answer

Question 12:

Show that the relation in the set A = {1, 2, 3, 4, 5}, given by :
R = {(a, b) : | a – b | is even} is an equivalence relation.
Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.

Answer:

Show Answer

Question 13:

Show that each of the relation R in the set :
A = {x : x $\in$ Z, 0 $\leq$ x $\leq$ 12}, given by :
(i) R = {(a, b) : | a – b | is a multiple of 4}
(ii) R = {(a, b) : a = b}
is an equivalence relation.
Find the set of all elements related to 1 in each case.

Answer:

Here

Show Answer

Question 14:

Give an example of a relation, which is :
Symmetric but neither reflexive nor transitive

Answer:

Let A = {1, 2, 3}.
The relation R = {(2, 3), (3, 2)} is symmetric but neither reflexive nor transitive.
[ $∴$ (1, 1) $\notin$ R; (2, 3), (3, 2) $\in$ R but (2, 2) $\notin$ R]

Show Answer

Question 15:

Give an example of a relation, which is :
Transitive but neither reflexive nor symmetric

Answer:

Let A = {1, 2, 3}.
The relation R = {(1, 3), (3, 2), (1, 2)} is transitive but neither reflexive nor symmetric.
[ $∴$ (1, 1) $\notin$ R; (1, 3) $\in$ R but (3, 1) $\notin$ R]

Show Answer

Question 16:

Give an example of a relation, which is :
Reflexive and symmetric but not transitive

Answer:

Let A = {1, 2, 3}.
The relation R = {(1, 1), (2, 2), (3, 3), (2, 3), (3, 2), (1, 2), (2, 1)}
is reflexive and symmetric but not transitive.
[ $∴$ (1, 2) and (2, 3) $\in$ R but (1, 3) $\notin$ R]

Show Answer

Question 17:

Give an example of a relation, which is :
Reflexive and transitive but not symmetric

Answer:

Let A = {1, 2, 3}.
The relation R = {(1, 1), (2, 2), (3, 3), (1, 2)} is reflexive and transitive but not symmetric.
[ $∴$ (1, 2) $\in$ R but (2, 1) $\notin$ R]

Show Answer

Question 18:

Give an example of a relation, which is :
Symmetric and transitive but not reflexive

Answer:

Let A = {1, 2, 3}.
The relation R = {(1, 2), (2, 1), (1, 1), (2, 2)} is symmetric and transitive but not reflexive. [ $∴$ (3, 3) $\notin$ R]

Show Answer

Question 19:

Show that the relation R in the set A of points in a plane, given by :
R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin} is an equivalence relation.
Further, show that the set of all points related to a point P $\neq$ (0, 0) is the circle passing through A with origin as centre.

Answer:

Show Answer

Question 20:

Show that the relation R, defined by the set A of all triangles as :
R = {(T₁, T₂) : T₁ is similar to T₂] is an equivalence relation.
Consider three right angle triangles T₁ with sides 3, 4, 5; T₂ with sides 5, 12, 13 and T₃ with sides 6, 8, 10.
Which triangles among T₁, T₂ and T₃ are related?

Answer:

Here

\Rightarrow

T₁ is related to T₃ and T₃ is related to T₁

\Rightarrow

(T₁, T₃)

\in

R.

Show Answer

Question 21:

Show that the relation related to R, defined in the set of all polygons as :
R = {(P₁, P₂), P₁ and P₂ have same number of sides} is an equivalence relation.
What is the set of all elements in A related to the right triangle T with sides 3, 4 and 5 ?

Answer:

Show Answer

Question 22:

Let L be the set of all lines in XY-plane and R is the relation in L defined as :
R = {(L₁, L₂) : L₁ is parallel to L₂}.
Show that R is an equivalence relation.
Find the set of all lines related to the line y=2x + 4.

Answer:

We have :

Show Answer

Question 23:

Choose the correct answer :
Let R be the relation in the set {1, 2, 3, 4} given
by : R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}.

R is reflexive and symmetric but not transitive
R is reflexive and transitive but not symmetric
R is symmetric and transitive but not reflexive
R is an equivalence relation

Answer:

R is reflexive and transitive but not symmetric

Show Answer

Question 24:

Choose the correct answer :
Let R be the relation in the set N given by :
R = {(a, b) : a = b – 2, b > 6}.

(2, 4) $\in$ R
(3, 8) $\in$ R
(6, 8) $\in$ R
(8, 7) $\in$ R.

Answer:

(6, 8) $\in$ R

Show Answer

Question 25:

Show that the function f : R_* $\to$ R_* defined by

is one-one and onto, where R_* is the set of all nonzero real numbers. Is the result true if the domain R_* is replaced by N with co-domain having same as R_* ?

Answer:

Let x₁, x₂ $\in$ R_*.

Show Answer

Question 26:

Check the injectivity and surjectivity of the following function :
f : N $\to$ N given by f (x) = x²

Answer:

Let x₁, x₂ $\in$ N.

$\Rightarrow$ − + (x₂ x₁ ) (x₂ x₁ ) = 0 $\Rightarrow$ x₂ – x₁ = 0
[ $∴$ x₁, x₂ $\in$ N $∴$ x₁ + x₂ $\neq$ 0]
$\Rightarrow$ x₁ = x₂ $\Rightarrow$ f is one-one
$\Rightarrow$ f is injective.
Now range of f = {1², 2², 3², ...}
= {1, 4, 9, ...} $\neq$ N
$\Rightarrow$ f is not onto $\Rightarrow$ f is not surjective.

Show Answer

Question 27:

Check the injectivity and surjectivity of the following function :
f : Z $\to$ Z given by f (x) = x²

Answer:

Let x₁, x₂ $\in$ Z.

$\Rightarrow$ x₁ = x₂ or x₁ = – x₂
$\Rightarrow$ x₂ = x₁ or x₂ = – x₁.
Thus f (x₁) = f (– x₁) −∨
x₁ $\in$ Z
$\Rightarrow$ f is not one-one $\Rightarrow$ f is not injective.
Also range of f = {0, 1², 2², ...} = {0, 1, 4, ...} $\neq$ Z
$\Rightarrow$ f is not onto $\Rightarrow$ f is not surjective.

Show Answer

Question 28:

Check the injectivity and surjectivity of the following function :
f : R $\to$ R given by f (x) = x²

Answer:

Let x₁, x₂ $\in$ R.
As in part (ii), f is not injective.
Also range of f = {0, 1², 2², ...}
= {0, 1, 4, ...} $\neq$ R
$\Rightarrow$ f is not onto $\Rightarrow$ f is not surjective.

Show Answer

Question 29:

Check the injectivity and surjectivity of the following function :
f : N $\to$ N given by f (x) = x³

Answer:

Let x₁, x₂ $\in$ N.

$\Rightarrow$ f is one-one $\Rightarrow$ f is injective.
Now range of f = {1³, 2³, 3³, ...} = {1, 8, 27, ...} $\neq$ N
$\Rightarrow$ f is not onto $\Rightarrow$ f is not surjective.

Show Answer

Question 30:

Check the injectivity and surjectivity of the following function :
f : Z $\to$ Z given by f (x) = x³

Answer:

Let x₁, x₂ $\in$ Z.
As in part (iv), f is injective.
Now range of f = {1³, 2³, 3³, ...} = {1, 8, 27, ...} $\neq$ Z
$\Rightarrow$ f is not onto $\Rightarrow$ f is not surjective.

Show Answer

Question 31:

Show that the Greatest Integer Function f : R $\to$ R given by :
f (x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.

Answer:

Show Answer

Question 32:

Show that the Modulus Function f : R $\to$ R, given by :
f (x) = | x |
is neither one-one nor onto, where | x | is x, if x is positive and | x | is – x, if x is negative.

Answer:

Show Answer

Question 33:

Show that the Signum function f : R $\to$ R given by :

is neither one-one nor onto.

Answer:

Since f (x) =1 for all x $\in$ (0, $\infty$ )
and f (x) = – 1 for all x $\in$ (– $\infty$ , 0),
$∴$ f is many-one $\Rightarrow$ f is not one-one.
Also range of f = {– 1, 0, 1) $\neq$ R
$\Rightarrow$ f is not onto.

Show Answer

Question 34:

Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4),
(2, 5), (3, 6)} be a function from A to B. Show that f is oneone.

Answer:

We have : f = {(1, 4), (2, 5), (3, 6)}.
Then f (1) = 4, f (2) = 5 and f (3) = 6
$\Rightarrow$ Different points of domain correspond to different f-images in the range.
Hence, f is one-one.

Show Answer

Question 35:

In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
(i) f : R $\to$ R defined by f (x) = 3 – 4x
(ii) f : R $\to$ R defined by f (x) = 1 + x².

Answer:

(i) Let x₁, x₂ $\in$ R.
Now f (x₁) = f (x₂)
$\Rightarrow$ 3 – 4x1 = 3 – 4x2
$\Rightarrow$ x₁ = x₂ $\Rightarrow$ f is one-one.
Let y $\in$ R. Let y = f (x₀).

$∴$ For each y $\in$ R, there exists x0 $\in$ R such that f (x0) = y.
$∴$ f is onto.
Hence, ‘f’ is one-one and onto or bijective.
(ii) Here f (1) = 1 + 1 = 2,
f (– 1) = 1 + 1 = 2.
Now 1 $\neq$ – 1 but f (1) = f (– 1)
$∴$ f is not one-one.
Also range of f is [1, $\infty$ ) $\neq$ R
$∴$ f is not onto.
Hence, ‘f’ is not bijective.

Show Answer

Question 36:

Let A and B be sets. Show that :
f : A × B $\to$ B × A such that f (a, b) = (b, a) is a bijective function.

Answer:

(a₁, b₁), (a₂, b₂) $\in$ A × B such that
f (a₁ , b₁ ) = (a₂, b₂ )
$\Rightarrow$ (b₁ , a₁ ) = (b₂, a₂ )
$\Rightarrow$ b₁ = b₂ and = a₁ = a₂
$\Rightarrow$ (a₂, b₂ ) = (a₁ , b₁ )
$∴$ f is one-one.
And corresponding to each ordered pair (y, x) $\in$ B × A,
there exists (x, y) $\in$ (A × B) such that
f (x, y) = (y, x)
$∴$ f is onto.
Hence, ‘f ’is a bijective function.

Show Answer

Question 37:

Let f : N $\to$ N be defined by :

State whether the function f is onto, one-one or bijective. Justify your answer.

Answer:

Show Answer

Question 38:

Let A = R – {3} and B = R – {1}.
Consider the function f : A $\to$ B defined by :

Is f one-one and onto ? Justify your answer.

Answer:

Let x₁, x₂ $\in$ R – {3}.
Now 1 f (x ) = f (x₂ )

$\Rightarrow$ f is onto.
Hence, ‘f’ is one-one and onto.

Show Answer

Question 39:

Choose the correct answer :
Let f : R $\to$ R be defined as f (x) = x⁴.

f is one-one onto
f is many-one onto
f is one-one but not onto
f is neither one-one nor onto.

Answer:

f is neither one-one nor onto.

Show Answer

Question 40:

Choose the correct answer.
Let f : R $\to$ R be defined as f (x) = 3x.

f is one-one onto
f is many one onto
f is one-one but not onto
f is neither one-one nor onto.

Answer:

f is one-one onto

Show Answer

Question 41:

Let f : {1, 3, 4} $\to$ {1, 2, 5} and g : {1, 2, 5} $\to$ {1, 3}
be given by :
f = {(1, 2), (3, 5), (4, 1)
and g = {(1, 3), (2, 3), (5, 1)}.
Write down gof.

Answer:

We have : f : {1, 3, 4} $\to$ {1, 2, 5}
and g : {1, 2, 5} $\to$ {1, 3}.
Here f (1) = 2, f (3) = 5 and f (4) = 1
and g (1) = 3, g (2) = 3 and g (5) = 1.
Here Rf = {1, 2, 5} = Dg
$∴$ Dgof = Df = {1, 3, 4}.
Now (gof) (1) = g (f (1)) = g (2) = 3
(gof) (3) = g (f (3)) = g (5) = 1
and (gof) (4) = g (f (4)) = g (1) = 3.
Hence, (gof) : {(1, 3), (3, 1), (4, 3)}.

Show Answer

Question 42:

Let f, g and h be functions from R to R. Show that :
(i) (f + g) oh = foh + goh
(ii) (f.g) oh = (foh) . (goh).

Answer:

(i) For all x $\in$ R,
[( f + g) oh] (x) = ( f + g) (h(x))
= f (h(x))+g(h(x))= ( foh) (x)+(goh)(x)
=[( foh)+(goh)] (x).
Hence, ( f + g) oh = foh+ goh.
(ii) For all x $\in$ R,
(( f .g) oh) x = ( f .g) (h(x))
= f (h(x)) g (h(x))
= ( foh) (x) . (goh) (x)
= [( foh) . (goh)] (x).
Hence ( f .g) oh = ( foh) . (goh) .

Show Answer

Question 43:

Find gof and fog, if :
(i) f (x) = | x | and g (x) = | 5x – 2 |
(ii) f (x) = 8x³ and g (x) = x^1/3.

Answer:

(i) (a) gof (x)= g ( f (x))
= g (|x|) = |5|x|−2|.
(b) fog (x) = f (g (x)) = f (|5x −2|)
= |5x −2|.
(ii) (a) gof (x) = g ( f (x)) = g(8x³ )
=(8x³)^1/3 =2x .
(b) fog (x) = f (g (x))
f(x^1/3) = 8(x^1/3)³ =8x

Show Answer

Question 44:

Answer:

Show Answer

Question 45:

State with reasons whether following functions have inverse :
(i) f : {1, 2, 3, 4} $\to$ {10} with
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} $\to$ {1, 2, 3, 4} with
g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h : {2, 3, 4, 5} $\to$ {7, 9, 11, 13} with
h = {(2, 7), (3, 9), (4, 11), (5, 13)}.

Answer:

(i) Here f (1) = f (2) = f (3) = f (4) = 10,
$∴$ f is not one-one
[ $∴$ 1, 2, 3, 4 have same image 10]
$\Rightarrow$ f is many-one
$\Rightarrow$ f has no inverse.
(ii) Here f (5) = f (7) = 4
$∴$ f is not one-one [ $∴$ 5 and 7 have same image 4]
$\Rightarrow$ f is many-one
$\Rightarrow$ f has no inverse.
(iii) Here each element of {2, 3, 4, 5} has a unique element in {7, 9, 11, 13}.
Similarly each element of {7, 9, 11, 13} has a unique preimage in {2, 3, 4, 5}.
$\Rightarrow$ h is one-one onto $\Rightarrow$ f is invertible.
Hence, ‘h’ has the inverse.

Show Answer

Question 46:

Show that : f [– 1, 1] $\to$ R given by :

Answer:

f (x₁) = f (x₂ )

Show Answer

Question 47:

Consider f : R $\to$ R given by f (x) = 4x + 3. Show that f is invertible.
Find the inverse of f.

Answer:

We have : f (x) = 4x + 3.

Show Answer

Question 48:

Let f : R $\to$ R be defined by f (x) = 3x – 7. Show that f is invertible.
Find f ^–1 : R $\to$ R.

Answer:

We have : f (x) = 3x – 7.
Now f (x₁) = f (x₂ )
$\Rightarrow$ 3x₁ – 7 = 3x₂ – 7
$\Rightarrow$ x₁ = x₂ $\Rightarrow$ f is one-one
$\Rightarrow$ f is invertible.
Let y = f (x) = 3x – 7

Show Answer

Question 49:

Consider R $\to$ [4, $\infty$ ) given by f (x) = x² + 4. Show that f is invertible with the inverse –1 f of f given by f ^–1 (y) =

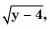
where R_* is the set of all nonnegative

real numbers.

Answer:

f (x₁)= f (x₂)

Show Answer

Question 50:

Consider f : R $\to$ [– 5, $\infty$ ), given by :
f (x) = 9x² + 6x – 5.

Answer:

f (x₁) = f (x₂ )

Show Answer

Question 51:

Let f : X $\to$ Y be an invertible function. Show that f has unique inverse.

Answer:

Since f is invertible, [Given]
$∴$ f is one-one onto.
If ‘g’ be the inverse of ‘f’, then
gof (x) = I_X and fog (y) = I_Y.
Let ‘g₁’, and ‘g₂’ be two inverses of ‘f’.
$∴$ fog₁ (y) = I_Y and fog2 (y) = I_Y
$\Rightarrow$ g₁ (y) = g₂ (y)
[Q f is one-one onto]
Hence ‘f’ has a unique inverse.

Show Answer

Question 52:

Consider f : {1, 2, 3} $\to$ {a, b, c}, given by :
f (1) = a, f (2) = b and f (3) = c.
Find f ^–1 and show that (f ^–1 )^–1 = f.

Answer:

We have : f (1) = a, f (2) = b, f (3)= c.
Thus f = {(1, a), (2, b), (3, c)}.
Clearly, f is one-one $\Rightarrow$ f is invertible
and 1 = f⁻¹ (a), 2 = f⁻¹ (b),
3 = f⁻¹ (c)
$\Rightarrow$ f⁻¹ : {a, b, c} $\to$ {1, 2, 3}.
Clearly, f⁻¹ is one-one and onto
and ( f⁻¹)⁻¹ ={(1, a), (2, b), (3, c)}
[ $∴$ f⁻¹ = {(a, 1), (b, 2), (c, 3)}]
$\Rightarrow$ ( f ⁻¹)⁻¹ = f.

Show Answer

Question 53:

Let f : X $\to$ Y be an invertible function. Show that the inverse of f^–1 is f i.e. (f^–1 )^–1 = f.

Answer:

f : X $\to$ Y is invertible
$\Rightarrow$ f is one-one and onto.

$\Rightarrow$ g = x.
Hence ( f₋₁)₋₁ = f.

Show Answer

Question 54:

If f : R $\to$ R be given by f (x) = (3 – x₃ )_1/3 , then f of (x) is :

x^1/3
x³
x
(3 – x³ )

Answer:

x

Show Answer

Question 55:

Answer:

Show Answer

Question 56:

Let R be the relation in the set {1, 2, 3, 4}, given by :
R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}.
Then :

R is reflexive and symmetric but not transitive
R is reflexive and transitive but not symmetric
R is symmetric and transitive but not reflexive
R is an equivalence relation.

Answer:

R is reflexive and transitive but not symmetric

Show Answer

Question 57:

Let R be the relation in the set N given by :
R = {(a, b) : a = b – 2, b > 6}.
Then :

(2, 4) $\in$ R
(3, 8) $\in$ R
(6, 8) $\in$ R
(8, 7) $\in$ R.

Answer:

(6, 8) $\in$ R

Show Answer

Question 58:

Let A = {1, 2, 3}. Then number of relations containing {1, 2} and {1, 3}, which are reflexive and symmetric but not transitive is :

1
2
3
4

Answer:

1

Show Answer

Question 59:

Let A = {1, 2, 3}. Then the number of equivalence relations containing (1, 2) is :

1
2
3
4

Answer:

2

Show Answer

Question 60:

Let f : R $\to$ R be defined as f (x) = x⁴. Then :

f is one–one onto
f is many–one onto
f is one–one but not onto
f is neither one–one nor onto.

Answer:

f is neither one–one nor onto.

Show Answer

Question 61:

Let f : R $\to$ R be defined as f (x) = 3x. Then :

f is one–one onto
f is many–one onto
f is one–one but not onto
f is neither one–one nor onto.

Answer:

f is one–one onto

Show Answer

Question 62:

If f : R $\to$ R be given by f (x) = (3 − x^31/3, then fof (x) is :

x^1/3
x³
x
3 – x³

Answer:

x

Show Answer

Question 63:

Answer:

Show Answer

Question 64:

Consider a binary operation ‘*’ on N defined as :
a * b = a³ + b³. Then :

is ‘*’ both associative and commutative ?
is ‘*’ commutative but not associative ?
is ‘*’ associative but not commutative ?
Is ‘*’ neither commutative nor associative ?

Answer:

is ‘*’ commutative but not associative ?

Show Answer

Question 65:

Number of binary operations on the set {a, b} is :

10
16
20
8

Answer:

16

Show Answer

NCERT Solutions for Class 12 Mathemetics Chapter 1 - Relations and Functions

Question 1:

Answer:

Question 2:

Answer:

Question 3:

Answer:

Question 4:

Answer:

Question 5:

Answer:

Question 6:

Answer:

Question 7:

Answer:

Question 8:

Answer:

Question 9:

Answer:

Question 10:

Answer:

Question 11:

Answer:

Question 12:

Answer:

Question 13:

Answer:

Question 14:

Answer:

Question 15:

Answer:

Question 16:

Answer:

Question 17:

Answer:

Question 18:

Answer:

Question 19:

Answer:

Question 20:

Answer:

Question 21:

Answer:

Question 22:

Answer:

Question 23:

Answer:

Question 24:

Answer:

Question 25:

Answer:

Question 26:

Answer:

Question 27:

Answer:

Question 28:

Answer:

Question 29:

Answer:

Question 30:

Answer:

Question 31:

Answer:

Question 32:

Answer:

Question 33:

Answer:

Question 34:

Answer:

Question 35:

Answer:

Question 36:

Answer:

Question 37:

Answer:

Question 38:

Answer:

Question 39:

Answer:

Question 40: