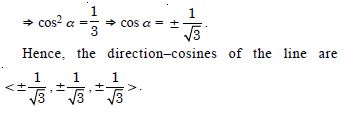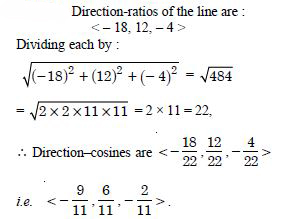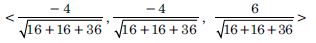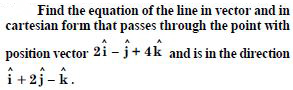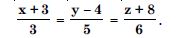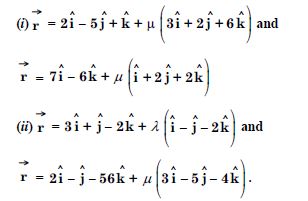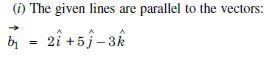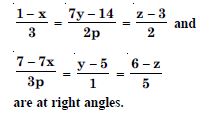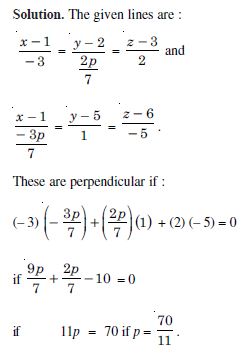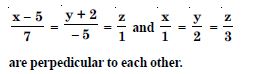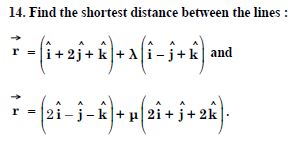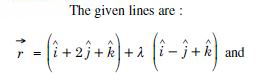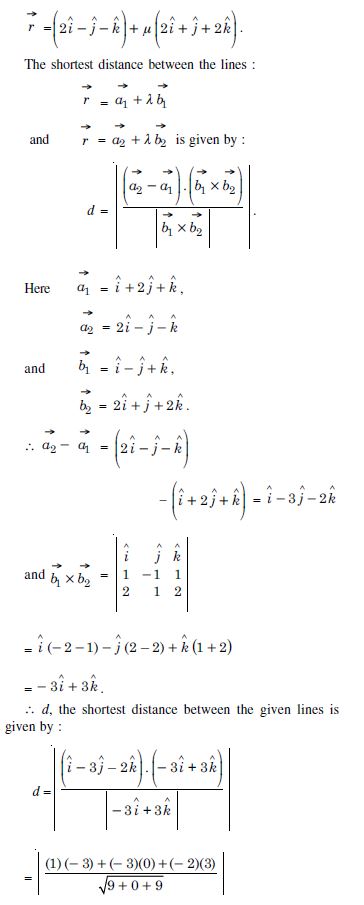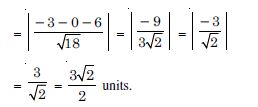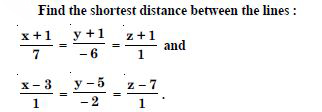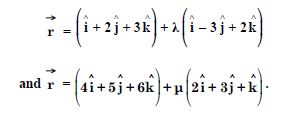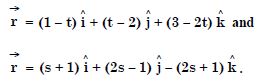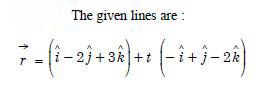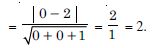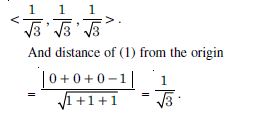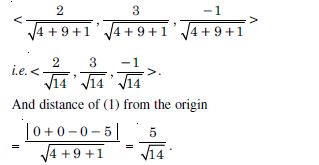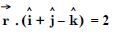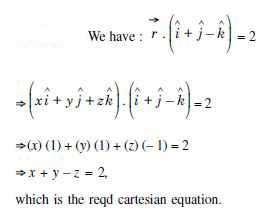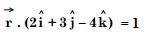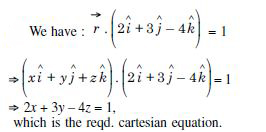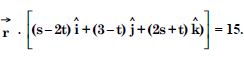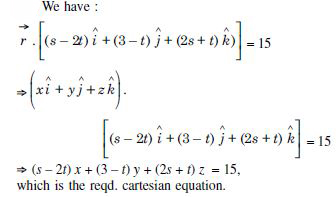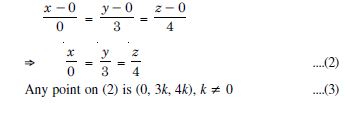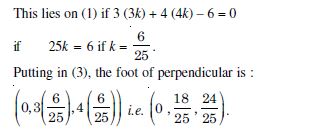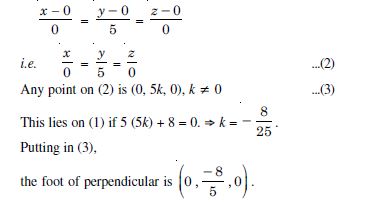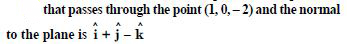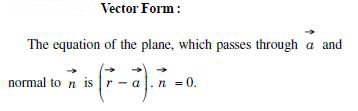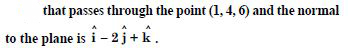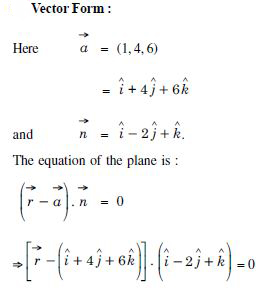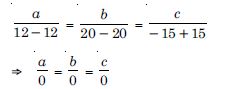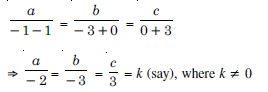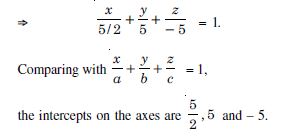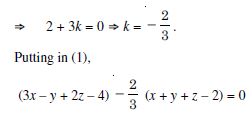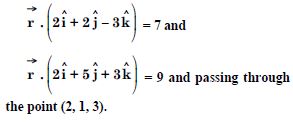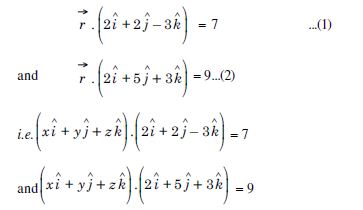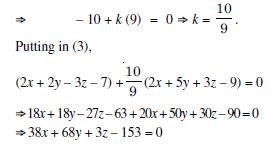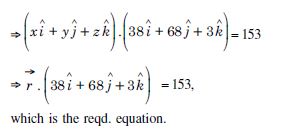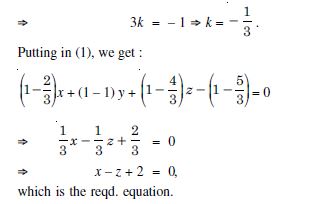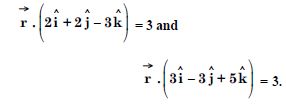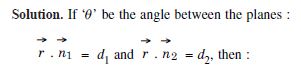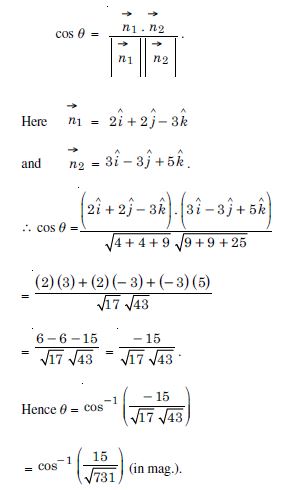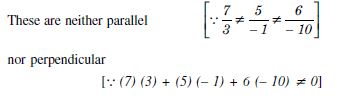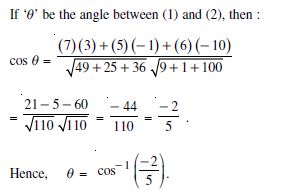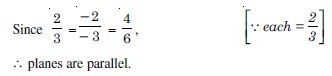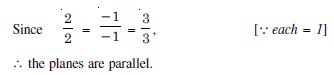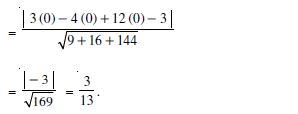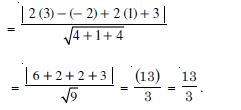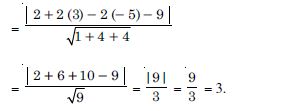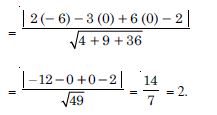Question 1:
If a line makes angles 90, 135, 45 with the x, y and z-axes respectively, find its direction-cosines.
Answer:
Direction–angles are 90, 135, 45.
Direction–cosines are < cos 90, cos 135, cos 45 >
Question 2:
Find the direction-cosines of a line, which makes equal angles with the co-ordinate axes.
Answer:
Let each directional angle be ‘’.
Direction–cosines are < cos , cos , cos >.
But l2 + m2 + n2 = 1
cos2 + cos2 + cos2 = 1 3 cos2 = 1
Question 3:
If a line has direction ratios – 18, 12, – 4, then what are its direction-cosines ?
Answer:
Question 4:
Show that the points :
(2, 3, 4) ; (– 1, – 2, 1) ; (5, 8, 7) are collinear.
Answer:
Let A (2, 3, 4); B (– 1, – 2, 1) and C (5, 8, 7) be the given points.
Direction-ratios of AB are :
< – 1 – 2, – 2 – 3, 1 – 4 >
i.e.< – 3, – 5, – 3 > i.e. < 3, 5, 3 >
Direction-ratios of BC are :
< 5 – (– 1), 8 – (– 2), 7 – 1 >
i.e. < 6, 10, 6 > i.e.< 3, 5, 3 >
AB and BC have same direction-ratios
AB || BC.
But B is a common point.
Hence, A, B, C are collinear.
Question 5:
Find the direction-cosines of the sides of the triangle whose vertices are :
(3, 5, – 4), (– 1, 1, 2) and (– 5, – 5, – 2).
Answer:
Let A (3, 5, – 4), B (– 1, 1, 2) and C (– 5, – 5, – 2) be the vertices of ΔABC.
Now (I) Direction–ratios of AB are
< – 1 – 3, 1 – 5, 2 – (– 4) >
i.e. < – 4, – 4, 6 >
Direction-cosines of AB are :
Question 6:
Answer:
Question 7:
Show that the line through the points (1, – 1, 2), (3, 4, – 2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Answer:
If A (1, – 1, 2) and B (3, 4, – 2) be the given points, then the direction–ratios of AB are :
< 3 – 1, 4 – (– 1), – 2 – 2 > i.e. < 2, 5, – 4 >.
Again if C (0, 3, 2) and D (3, 5, 6) be the given points,
then the direction ratios of CD are :
< 3 – 0, 5 – 3, 6 – 2 > i.e. < 3, 2, 4 >.
Now AB is perp. to CD if :
(2) (3) + (5) (2) + (– 4) (4) = 0
[a1a2 + b1b2 + c1c2 = 0]
i.e. if 6 + 10 – 16 = 0, which is true.
Hence, AB is perpendicular to CD.
Question 8:
Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (– 1, – 2, 1), (1, 2, 5).
Answer:
If A (4, 7, 8) and B (2, 3, 4) be the given points, then the direction-ratios of AB are :
< 2 – 4, 3 – 7, 4 – 8 > i.e. < – 2, – 4, – 4 >
i.e. < 1, 2, 2 >.
If C (– 1, – 2, 1) and D (1, 2, 5) be the given points, then
the direction–ratios of CD are :
< 1 – (– 1), 2 – (– 2), 5 – 1 > i.e. < 2, 4, 4 >
i.e. < 1, 2, 2 >.
AB is parallel to CD if :
Question 9:
Answer:
Question 10:
Answer:
Question 11:
Find the cartesian equation of the line, which passes through the point (– 2, 4, – 5) and parallel to the line given
by :
Answer:
The given line is :
Question 12:
Answer:
Question 13:
Find the vector and cartesian equations of the line that passes through the origin and (5, –2, 3).
Answer:
(i) The vector equations of the line is :
Question 14:
Find the vector and the cartesian equation of the line that passes through the points (3, – 2, – 5), (3, – 2, 6).
Answer:
Question 15:
Find the angle between the following pairs of lines :
Answer:
Question 16:
Answer:
Question 17:
Find the value of ‘p’ so that the lines :
Answer:
Question 18:
Show that the lines :
Answer:
Question 19:
Answer:
Question 20:
Answer:
Question 21:
Find the shortest distance between the lines whose vector equations are :
Answer:
Question 22:
Find the shortest distance between the following lines whose vector equations are :
Answer:
Question 23:
In each of the following, determine the direction– cosines of the normal to the plane and the distance from the
origin :
z = 2
Answer:
The given plane is z = 2 ....(1)
Direction-cosines of the normal to the plane are < 0, 0, 1 >.
And distance of (1) from the origin
Question 24:
In each of the following, determine the direction– cosines of the normal to the plane and the distance from the
origin :
x + y + z = 1
Answer:
The given plane is x + y + z = 1 ....(1)
Direction-ratios of the normal to the plane are : < 1, 1, 1 >
Direction-cosines of the normal to the plane are
Question 25:
In each of the following, determine the direction– cosines of the normal to the plane and the distance from the
origin :
2x + 3y – z = 5
Answer:
The given plane is 2x + 3y – z = 5 ....(1)
Direction–ratios of the normal to the plane are < 2, 3, – 1 >.
Direction–cosines of the normal to the plane are :
Question 26:
In each of the following, determine the direction– cosines of the normal to the plane and the distance from the
origin :
5y + 8 = 0.
Answer:
The given plane is 5y + 8 = 0 ....(1)
Direction–ratios of the normal to the plane are < 0, 5, 0 >
i.e. < 0, 1, 0 >
Direction–cosines of the normal to the plane are < 0, 1, 0 > .
Question 27:
Answer:
Question 28:
Find the cartesian equation of the following planes :
Answer:
Question 29:
Find the cartesian equation of the following planes :
Answer:
Question 30:
Find the cartesian equation of the following planes :
Answer:
Question 31:
In the following cases, find the co-ordinates of the foot of the perpendicular drawn from the origin :
2x + 3y + 4z – 12 = 0
Answer:
The given plane is :
2x + 3y + 4z – 12 = 0 ...(1)
Direction-ratios of the normal to the plane are :
< 2, 3, 4 >
The equations of the normal through (0, 0, 0) are :
Question 32:
In the following cases, find the co-ordinates of the foot of the perpendicular drawn from the origin :
3y + 4z – 6 = 0
Answer:
The given plane is 3y + 4z – 6 = 0 ....(1)
Direction-ratios of the normal are < 0, 3, 4 >.
The equations of the normal though (0, 0, 0) are :
Question 33:
In the following cases, find the co-ordinates of the foot of the perpendicular drawn from the origin :
x + y + z = 1
Answer:
The given plane is :
x + y + z = 1 ....(1)
Direction-ratios of the normal to the plane are < 1, 1, 1 >.
Question 34:
In the following cases, find the co-ordinates of the foot of the perpendicular drawn from the origin :
5y + 8 = 0
Answer:
The given plane is :
5y + 8 = 0 ...(1)
Direction-ratios of the normal to the plane < 0, 5, 0 >
The equations of the normal through (0, 0, 0) are :
Question 35:
Find the vector and cartesian equation of the plane :
Answer:
Question 36:
Find the vector and cartesian equation of the plane :
Answer:
Question 37:
Find the equation of the plane that passes through three points :
(1, 1, – 1), (6, 4 – 5), (– 4, – 2, 3)
Answer:
Any plane through (1, 1, – 1) is :
a (x – 1) + b (y – 1) + c (z + 1) = 0....(1)
Since the plane passes through the points
(6, 4, – 5) and (– 4, – 2, 3),
a (6 – 1) + b (4 – 1) + c (– 5 + 1) = 0
and a (– 4 – 1) + b (– 2 – 1) + c (3 + 1) = 0
5a + 3b – 4c = 0 ....(2)
and – 5a – 3b + 4c = 0 ....(3)
Solving (2) and (3),
a, b, c can’t be found.
Since the points are collinear,
an infinite number of planes can be found through the given points.
Question 38:
Find the equation of the plane that passes through three points :
(1, 1, 0), (1, 2, 1), (– 2, 2, – 1).
Answer:
Any plane through (1, 1, 0) is :
a (x – 1) + b (y – 1) + cz = 0 ....(1)
Since the plane passes through the points
(1, 2, 1) and (– 2, 2, – 1),
a (1 – 1) + b (2 – 1) + c (1) = 0
and a (– 2 – 1) + b (2 – 1) + c (– 1) = 0
0 . a + b + c = 0 ....(2)
and – 3a + b – c = 0 ....(3)
Solving (2) and (3),
Putting these values of a, b, c in (1), we get :
– 2k (x – 1) – 3k (y – 1) + 3kz = 0
–2 (x – 1) – 3 (y – 1) + 3z = 0 [ k 0]
– 2x + 2 – 3y + 3 + 3z = 0
2x + 3y – 3z = 5,
which is the reqd. equation.
Question 39:
Find the intercepts cut off by the plane : 2x + y – z = 5 with the axes.
Answer:
The given equation of the plane is :
2x + y – z = 5
Question 40:
Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane.
Answer:
Clearly the plane passes through the point (0, 3, 0).
The direction-cosines of the normal to the plane are < 0, 1, 0 >
The equation of the plane is :
0 . (x – 0) + 1 . (y – 3) + 0 . (z – 0) = 0
y – 3 = 0 y = 3.
Question 41:
Find the equation of the plane through the intersection of the planes :
3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Answer:
The given planes are :
3x – y + 2z – 4 = 0 ...(1)
and x + y + z – 2 = 0 ...(2)
Any plane through the intersection of (1) and (2) is :
(3x – y + 2z – 4) + k (x + y + z – 2) = 0 ...(3)
Since it passes thro’ (2, 2, 1).
(6 – 2 + 2 – 4) + k (2 + 2 + 1 – 2) = 0
7x – 5y + 4z – 8 = 0,
which is the reqd. equation.
Question 42:
Find the vector equation of the plane passing through the intersection of the planes :
Answer:
The given planes are :
i.e. 2x + 2y – 3z – 7 = 0 ...(1)′
and 2x + 5y + 3z – 9 = 0 ...(2)′
Any plane through the intesection of (1)′ and (2)′ is :
(2x + 2y – 3z – 7) + k (2x + 5y + 3z – 9) = 9...(3)
Since it passes thro’ (2, 1, 3),
(4 + 2 – 9 – 7) + k (4 + 5 + 9 – 9) = 0
Question 43:
Find the equation of the plane through the line of intersection of the planes :
x + y + z = 1 and 2x + 3y + 4z = 5,
which is perpendicular to the plane x – y + z = 0.
Answer:
Any plane through the line of intersection of
the planes :
x + y + z – 1 = 0 and 2x + 3y + 4z – 5 = 0 is :
(x + y + z – 1) + k (2x + 3y + 4z – 5) = 0
i.e.(1 + 2k) x + (1 + 3k) y + (1 + 4k) z
– (1 + 5k) = 0 ...(1)
Since it is perpendicular to the plane :
x – y + z = 0 ...(2)
their normals are perpendicular
(1 + 2k) (1) + (1 + 3k) (– 1) + (1 + 4k) (1) = 0
1 + 2k – 1 – 3k + 1 + 4k = 0
Question 44:
Find the angle between the planes whose vector equations are :
Answer:
Question 45:
In the following, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angles between them :
7x + 5y + 6z + 30 = 0 and
3x – y – 10z + 4 = 0
Answer:
The given planes are :
7x + 5y + 6z + 30 = 0 ...(1)
and 3x – y – 10z + 4 = 0 ...(2)
Question 46:
In the following, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angles between them :
2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
Answer:
The given planes are :
2x + y + 3z – 2 = 0 ....(1)
and x – 2y + 5 = 0 ....(2)
Since (2) (1) + (1) (– 2) + (3) (0) = 0,
planes are parallel.
Question 47:
In the following, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angles between them :
2x – 2y + 4z + 5 = 0 and
3x – 3y + 6z – 1 = 0
Answer:
The given planes are :
2x – 2y + 4z + 5 = 0 ....(1)
and 3x – 3y + 6z – 1 = 0 . ...(2)
Question 48:
In the following, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angles between them :
2x – y + 3z – 1 = 0 and
2x – y + 3z + 3 = 0
Answer:
The given planes are :
2x – y + 3z – 1 = 0 ....(1)
and 2x – y + 3z + 3 = 0 ....(2)
Question 49:
In the following, determine whether the given planes are parallel or perpendicular and in case they are neither, find the angles between them :
4x + 8y + z – 8 = 0 and y + z – 4 = 0.
Answer:
The given planes are :
4x + 8y + z – 8 = 0 ....(1)
and y + z – 4 = 0 ....(2)
Question 50:
In the following, find the distance of each of the given points from the corresponding given planes :
Point
(0, 0, 0)
Plane
3x – 4y + 12z = 3
Answer:
The given plane is :
3x – 4y + 12z – 3 = 0 ....(1)
Distance, of (0, 0, 0) from plane (1)
Question 51:
In the following, find the distance of each of the given points from the corresponding given planes :
Point
(3, – 2, 1)
Plane
2x – y + 2z + 3 = 0
Answer:
The given plane is :
2x – y + 2z + 3 = 0 ....(1)
Distance, (3, – 2, 1) from plane (1)
Question 52:
In the following, find the distance of each of the given points from the corresponding given planes :
Point
(2, 3, – 5)
Plane
x + 2y – 2z = 9
Answer:
The given plane is :
x + 2y – 2z – 9 = 0 ....(1)
Distance of (2, 3, – 5) from plane (1)
Question 53:
In the following, find the distance of each of the given points from the corresponding given planes :
Point
(– 6, 0, 0)
Plane
2x – 3y + 6z – 2 = 0
Answer:
The given plane is 2x – 3y + 6z – 2 = 0 ....(1)
Distance of (– 6, 0, 0) from place (1)
Question 54:
Distance between two planes :
2x + 3y + 4z = 5 and 4x + 6y + 8z = 12 is :
- 2 units
- 4 units
- 8 units
Answer:
Question 55:
The planes 2x – y + 4z = 3 and 5x – 2·5y + 10 z = 6 are :
- perpendicular
- parallel
- intersect along y-axis
Answer:
parallel