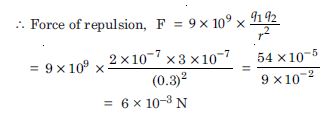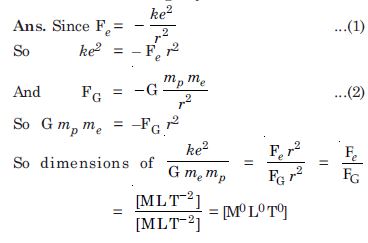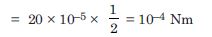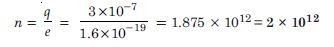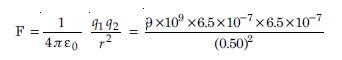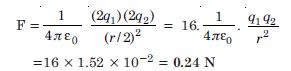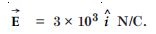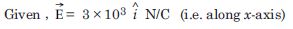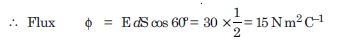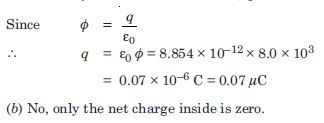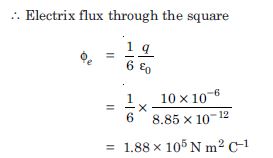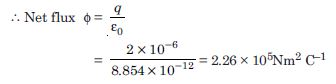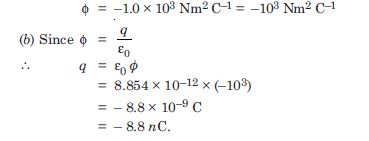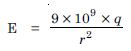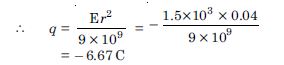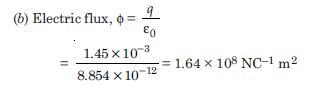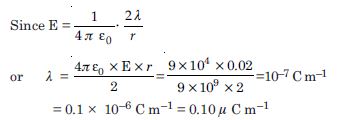Prepare for your Class 12th board examination with NCERT Solutions available for free at the Aasoka platform. These solutions will help students with competitive exam preparations as well. The NCERT Solutions for Class 12th is prepared by professionals who have years of experience. Students can enhance their understanding of the concept with the solutions on Aasoka, the top eLearning platform.
From the first chapter of Class 12th Physics “Electric Charges and Fields”, students get to learn about electric charge; Coulomb’s law force between two-point charges, conservation of charge, superposition principle and continuous charge distribution, forced between multiple charges, electric field, electric flux, uniformly charged infinite plane sheet, electric dipole, electric field lines, and so much more.
Question 1:
What is the force between two small charged spheres having charges of 2 × 10–7 C and 3 × 10–7 C placed 30 cm apart in air ?
Answer:
Given q1 = 2 × 10–7 C, q2 = 3 × 10–7 C, r = 30 cm = 0.3 m
Question 2:
The electrostatic force on a small sphere of charge 0.4 C due to another small sphere of charge –0.8 C in air is 0.2 N.
- What is the distance between the two spheres ?
- What is the force on the second sphere due to the first ?
Answer:
Given q1 = 0.4 C = 0.4 × 10–6 C
Question 3:
Check that the ratio ke2/G me mp is dimensionless. Look up a
table of physical constants and determine the value of this ratio.
What does the ratio signify ?
Answer:
Question 4:
Explain the meaning of the statement ‘electric charge of a body is quantised.’
Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large
scale charges ?
Answer:
Quantisation of charge. It is that property of charge by virtue of which charge on a body exists in the form of discrete packet of charge e, only, where e is the charge on an electron. The charge carried by anybody would be equal to ± ne, where n = 0, 1, 2, 3, 4, 5, etc. The charge on a body is thus some multiple of e and cannot exist as a fraction of e. So charge exists in the form of packets and not in continuous amounts. Thus, charge is said to have a discrete (discontinuous) nature or is said to be quantised.
At macroscopic level, we deal with charges that are enormous as compared to the magnitude of minimum charge i.e. e (1.6 × 10–19 C).
In this case, the increase and decrease in units of e is not very different from saying that charges are continuous. So at macroscopic level we can ignore quantisation of electric charge.
Question 5:
When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Answer:
When a glass rod is rubbed with silk, the charges developed on the glass rod and the piece of silk are equal and opposite. Similar is the case in other pair of bodies. So electric charge can neither be produced nor destroyed but simply transferred from one body to another, hence is consistent with the law of conservation of charge.
Question 6:
Four point charges qA = 2 C, qB = –5 C, qC = 2 C and qD = –5C are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1 C placed at the centre of the square ?
Answer:
ABCD is a square having charges qA = 2 C, qB = – 5C, qC = 2C, qD = –5 C at its corners and a charge 1 C is placed at the centre O.
Net force on q due to qB and qD = 0
So net force on q due to four charges is zero.
Question 7:
An electrostatic field line is a continuous curve. That is, a field line cannot have sudden
break. Why not ?
Explain why two field lines never cross each other at any point.
Answer:
The electric line of force starts from a positively charged body and ends at a negatively charged body and it carries information about the direction of electric field at different points in space, thus it cannot have sudden break.
Because if any two lines cross each other at any point, then the electric field at the point of intersection will not have a unique direction, which is impossible. Hence no two electric lines of force can intersect each other.
Question 8:
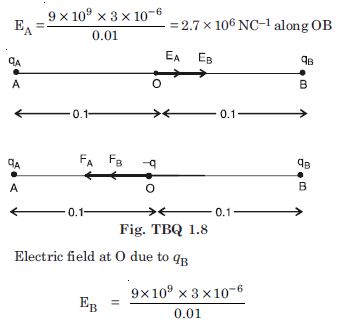
Two point charges qA = 3 C and qB = –3 C are located 20 cm apart in vacuum. What is the electric field at the mid point O of the line AB joining the two charges ?
If a negative test charge of magnitude 1.5 × 10–9C is placed at this point, what is the force experienced by the test charge ?
Answer:
Given q A = 3 C = 3 × 10–6 C qB = – 3 C = – 3 × 10–6 C r = 20 cm = 0.2 m Electric field at O due to qA
Question 9:
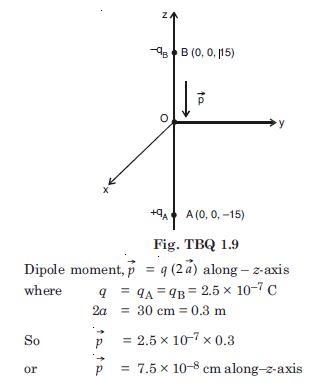
A system has two charges qA = 2.5 × 10–7 C and q B = –2.5 × 10–7 C located at A : (0, 0, –15 cm) and B : (0, 0, +15 cm) respectively. What is the total charge and electric dipole of the system ?
Answer:
Since electric dipole consists of two equal and opposite charges, Hence total charge = qA + qB = 0
Question 10:
An electric dipole with dipole moment 4 × 10 –9 C m is aligned at 30 with the direction of a uniform electric field of magnitude 5 × 10 4 NC –1. Calculate the magnitude of the torque acting on the dipole.
Answer:
Given p = 4 × 10–9 Cm, = 30, E = 5 × 104 NC–1, = ? Since = pE sin = 4 × 10–9 × 5 × 104 × sin 30
Question 11:
A polythene piece rubbed with wool is found to have a negative charge of 3 × 10 −7 C.
- Estimate the number of electrons transferred (from which to which).
- Is there a transfer of mass from wool to polythene ?
Answer:
(a) Charge on one electron = 1.6 × 10−19 C.
Number of electrons in the given charge
(b) Since wool gets negative charge on rubbing with
polythene, wool must gain electrons from polythene.
Ideally speaking there must be a transfer of mass
due to transfer of electrons but since the mass of
electron is very small, this transfer of mass may be
negligible (= 2 × 10–18 kg).
Question 12:
Two insulated charged copper spheres A and B have their centres separated by a distance of 50
cm.
(a) What is the mutual force of electrostatic repulsion if the charge on each is 6.5 ×
10−7 C ?
The radii of A and B are negligible as compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount and the
distance between them is halved ?
Answer:
(a) q1 = 6.5 × 10−7 C, q2 = 6.5 × 10−7 C, r = 50 cm = 0.50 m
(b) When each charge is doubled and the distance between them is reduced to half, then
Question 13:
Suppose the spheres A and B in Q. 1.10 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second and finally removed from both. What is the new force of repulsion between A and B ?
Answer:
Let A and B be two given spheres each having charge q = 6.5 × 10–7 C. When another sphere say C is placed in contact with the sphere A, the two will distribute the charges equally, Fig. TBQ 1.13 (a).
Question 14:
Figure TBQ 1.14 gives tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio ?
Answer:
Charges 1 and 2 are negative because the deflections are towards +vely charged plate. Particle 3 has the +ve because charge is deflected towards −vely charged plate. Particle 3 has the highest charge to mass ratio because the greater is the charge on the particle (or lesser is its mass) the more is its deflection.
Question 15:
Consider a uniform electric field
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to yz – plane ?
- What is the flux through the same square if the normal to its plane makes a 60 angle with the x-axis ?
Answer:
dS = 10 × 10 = 100 cm2 = 0.01 m2
Here = 0
Flux = E dS cos 0
= E dS = 3 × 103 × (0.01) = 30 Nm2 C–1
(b) Here = 60
Question 16:
What is the net flux of the uniform electric field of Exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes.
Answer:
Net flux over the cube is zero, because the number of lines entering the cube is the same as the number of lines leaving the cube.
Question 17:
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 103 Nm 2 /C.
- What is the net charge inside the box ?
- If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box ? Why or why not ?
Answer:
(a) Given
Question 18:
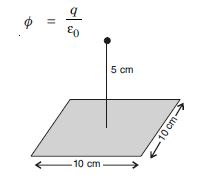
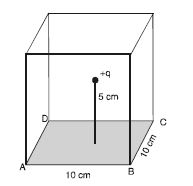
A point charge +10 C is at a distance 5 cm directly above the centre of a square of side 10 cm as shown in the figure. What is the magnitude of the electric flux through the square. [Hint. Think of the square on one face of a cube with edge 10 cm]
Answer:
Here we can imagine that the square ABCD as one face of a cube with edge 10 cm, and charge +q is placed at the centre of the cube as shown in the figure.
From Gauss’ theorem, electrix flux through all the faces of the cube
Question 19:
A point charge of 2.0 C is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electrix flux through the surface ?
Answer:
q = 2.0 C = 2 × 10–6 C
Question 20:
A point charge causes an electric flux of –1.0 × 103 N m2 C–1 to pass through spherical gaussian surface of 10.0 cm radius centred on the charge.
- If the radius of the gaussian surface were doubled, how much flux would pass through the surface ?
- What is the value of the point charge ?
Answer:
(a) The electric flux depend only on the charge present in the gaussian surface. So electric flux passing through the gaussian surface of double the radius will be the same i.e.
Question 21:
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 × 103 NC–1 and points radially inward, what is the net charge on the sphere ?
Answer:
Given E = –1.5 × 103 NC–1
[∵E is directed inwards]
r = 20 cm = 0.2 m, q = ?
Question 22:
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 C m–2.
- Find the charge on the sphere.
- What is the total electric flux leaving the surface of the sphere ?
Answer:
Given
= 80.0 Cm–2 = 80 × 10–6 C m–2
D = 2.4 m
or r = 1.2 m
(a) Charge on the sphere,
q = × 4 πr2
or q = 80 × 10–6 × 4 × 3.142 × (1.2)2 = 1.45 × 10–3 C
Question 23:
An infinite line charge produces a field of 9 × 104 NC–1 at a distance of 2 cm. Calculate the linear charge density.
Answer:
Given
E = 9 × 104 NC–1
r = 2 cm = 0.02 m
Question 24:
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 × 10–22 Cm–2.
Answer:
Given = 17.0 × 10–22 cm–2