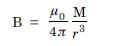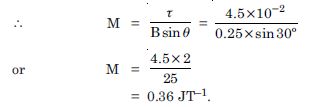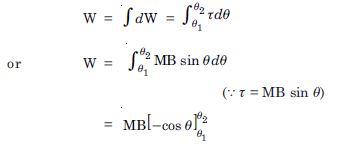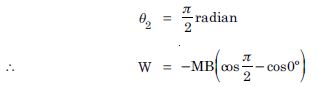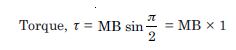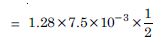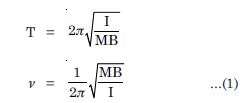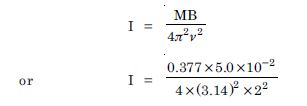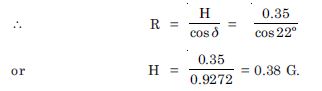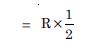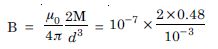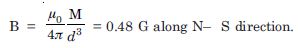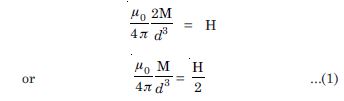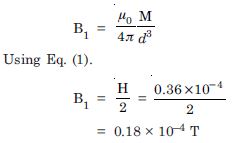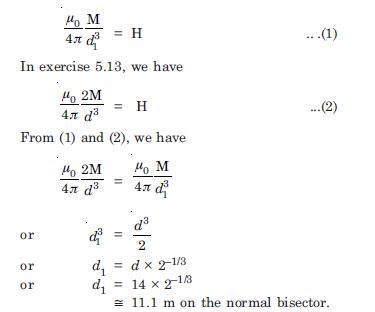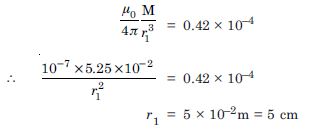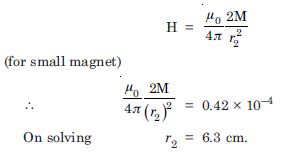Aasoka offers NCERT Solutions for Class 12th students for the chapter “Magnetism and Matter”. This aids in getting a better understanding of the concepts included in the chapter. The experts at Aasoka have designed the NCERT Solutions as per the latest syllabus and exam pattern decided by the board. Class 12th marks matter a lot, therefore, students have to work hard in order to achieve the scores required to get into the desired career in the future.
The fifth chapter of Class 12th Physics “Magnetism and Matter” includes topics such as compass direction and its effects at the poles, how to determine the magnetic field of the earth, interstellar space, magnetic moment of the solenoid, earth’s magnetism, magnetic field lines, etc.
Question 1:
Answer the following questions regarding earth’s magnetism :
A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth’s magnetic field.
The angle of dip at a location in southern Indian is about 18. Would you expect a greater or lesser dip angle in Britain ?
If you make a map of magnetic field lines at Melbourne in Australia, would the lines seen to go into the ground or come out of the ground ?
In which direction would a compass free to move in the vertical plane point to, if located right on the geomagnetic north or south pole ?
The earth’s field is claimed roughly approximately, the field due to a dipole magnetic moment 8 × 1022 JT–1 located at the centre. Check your order of magnitude of this number same way.
Geologists claim that besides the main magnetic NS poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all ?
Answer:
Magnetic declination, angle of dip, horizontal component of earth’s magnetic field.Greater angle of dip in Britain, (it is about 70°), because Britain is closer to the magnetic north pole. Field lines of B due to the earth’s magnetism would seem to come out of the ground.
A compass is free to move in a horizontal plane, while the earth’s field is exactly vertical at the magnetic poles. So the compass can point in any direction there.
Use the formula for field B on the normal bisector of a dipole of magnetic moment m.
Take M = 8 × 10 22 JT–1
r = 6.4 × 106 m ;
one gets B = 0.3 G
which checks with the order of magnitude of the
observed field on the earth.
The earth’s field is only approximately a dipole field. Local N–S poles may arise due to, for instance, magnetised minerals deposits.
Question 2:
Answer the following questions :
The earth’s magnetic field varies from point to point in space. Does it also change with time ? If so, on what time scale does it change appreciably ?
The earth’s core is known to contain iron. Yet geologists do not regard this as a source of earth’s magnetism. Why ?
The charged currents in the outer conducting regions of the earth’s core are thought to be responsible for earth’s magnetism. What might be the ‘battery’ (i.e. the source of energy) to sustain these currents ?
The earth may have ever reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth’s field in such distant past ?
The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion ?
Interstellar space has an extremely weak magnetic field of the order of 10–12 T. Can such a weak field of any significant consequence ? Explain.
Note : Exercise 5.2 is meant mainly to arouse your curiosity. Answer to some questions above are tentative or unknown. Brief answers wherever possible are given at the end. For detail, you should consult a good text on geomagnetism.
Answer:
Yes, it does change with time. Time scale for appreciable change is roughly a few hundred years. But even on a much smaller scale of a few years, its variations are not completely negligible. Because molten iron (which is the phase of iron at the high temperatures of the core) is not ferromagnetic.
One possibility is the radioactivity in the interior of the earth.
Earth’s magnetic field gets weakly ‘recorded’ in certain rocks during solidification. Analysis of this rock magnetism offers clues to geomagnetic history. At large distance, earth’s field gets modified due to the field of ions in motion (in the earth’s ionosphere). The latter is sensitive to extra terrestrial disturbance such as, for example, the solar wind. From the relation R = mυ/eB, an extremely minute field bends charged particles in a circle of very large radius. Over a small distance, the deflection due to the circular orbit of such large R may not be noticeable, but over the gigantic interstellar distances, the deflection can significantly affect the passage of e.g. cosmic rays.
Question 3:
A short bar magnet placed with its axis at 30 with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 × 10–2 J. What is the magnitude of magnetic moment of the magnet ?
Answer:
Given
= 30, B = 0.25 T
τ = 4.5 × 10 –2 J, M = ?
Since τ = MB sin
Question 4:
A short bar magnet of magnetic moment M = 0.32 JT–1 is placed in a uniform external magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientations would correspond to its (i) stable and (ii) unstable equilibrium ? What is the potential energy of the magnet in each case ?
Answer:
Given
M = 0.32 JT–1, B = 0.15 T
U = ?
= 0
(i) If
M
B , then we have stable equilibrium
and
U = – MB cos 0 = – 0.32 × 0.15 T
= – 4.8 × 10–2 J
(ii) If
M is anti-parallel to
B , we have unstable
equilibrium and
= 180
U = – MB cos 180
= 0.32 × 0.15 T
= 4.8 × 10 –2 J.
Question 5:
A closely wound solenoid of 800 turns and area of cross-section 2.5 × 10–4 m2 carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment ?
Answer:
Given N = 800, A = 2.5 × 10–4 m2
I = 3.0 A, M = ?
Since M = NIA
M = 800 × 3 × 2.5 × 10–4
or M = 0.60 JT–1 along the axis of the
solenoid.
Question 6:
If the solenoid in Exercise 5.5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of the torque on the solenoid when its axis makes an angle of 30 with the direction of the applied field ?
Answer:
Given
B = 0.25 T
= 30
Since τ = MB sin
= 0.6 × 0.25 × sin 30
= 7.5 × 10–2 Nm.
Question 7:
A bar magnet of magnetic moment
1.5 JT–1 lies aligned with the direction of a
uniform magnetic field of 0.22 T.
(a) What is the amount of work required by
an external torque to turn the magnet so as to
align its magnetic moment ?
normal to the field direction,
opposite to the field direction ?
What is the torque on the magnet in cases
(i) and (ii) ?
Answer:
M = 1.5 JT –1 B = 0.22 T
W = – MB (cos 2 – cos 1)
(a) (i) In this case 1 = 0
= MB (0 – 1) = MB
= 1.5 × 0.22 = 0.33 J
(ii) 1 = 0, 2 = radian
W = –MB (– 1 – 1) = 2 MB
= 2 × 0.33 = 0.66 J.
= 0.33 N
(ii) Torque, τ = MB sin
= MB × 0 = 0
Question 8:
A closely wound solenoid of 2000 turns and area of cross-section 1.6 × 10 –4 m 2, carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane. What is the magnetic moment associated with the solenoid ?
What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10–2 T is set up at an angle of 30 with the axis of the solenoid ?
Answer:
Magnetic dipole moment,
M = nIA
= 2000 × 4.0 × 1.6 × 10–4
= 1.28 JT–1
(b) Net force = 0
Torque, τ = MB sin
= 1.28 × 7.5 × 10–2 × sin 30
= 4.8 × 10–2 Nm.
Question 9:
A circular coil of 16 turns and radius 10 cm, carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 5.0 ×10–2 T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with frequency of 2.0 s–1. What is the moment of inertia of the coil about its axis of rotation ?
Answer:
Magnetic dipole moment of the coil.
M = NIA
or M = 16 × 0.75 × π(.10)2 Am2
= 0.377 Am2
Time period of oscillation is given by
Moment of inertia of the coil about the axis of rotation.
= 1.194 kg m2
= 1.2 kg m2.
Question 10:
A magnetic needle free to rotate in a vertical plane to the magnetic meridian has its north tip pointing down at 22 with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Answer:
Given
= 22, H = 0.35 G
R = ?
Since H = R cos
Question 11:
At a certain location in Africa, a compass point 12 west of the geographical north. The north tip of the magnetic needle of a dip circle placed in the plane of the magnetic meridian points 60 above the horizontal. The horizontal component of the earth’s field is measured to be 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Answer:
Dip, = 60
V = 0.16 G = 0.16 × 10–4T
Since V = R cos
0.16 × 10–4 = R. cos 60
R = 2 × 0.16 × 0–4
= 0.32 × 100–4 T
The earth’s field lies in a vertical plane 12 west
of the geographical meridian making an angle of 60
(upwards) with the horizontal (magnetic south to
magnetic north) direction.
Question 12:
A short bar magnet has a magnetic moment of 0.48 JT–1. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (i) the axis (ii) the equatorial line (normal bisector) of the magnet. Ans. Given M = 0.48 JT–1, d = 10 cm B = ? (i) Along the axis (for a short dipole)
Answer:
Given M = 0.48 JT–1, d = 10 cm B = ?
(i) Along the axis (for a short dipole)
= 0.96 × 10–4 T = 0.96 G along S–N direction
(ii) Along equatorial line (for a short dipole)
Question 13:
A short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north-south direction. Null points are found on the axis of the magnet at 14 cm from the centre of the magnet. The earth’s magnetic field at the place is 0.36 G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null point (i.e. 14 cm from the centre of the magnet) ?
Answer:
Given, d = 14 cm = 14 × 10–2 m
H = 0.36 G = 0.36 × 10–4 T
Since null points are found on the axis of the
magnet, so, we have
Now on equatorial line at same distance d, we have
Question 14:
If the bar magnet in Exercise 5.13 is turned around by 180, where will the new null point be located ?
Answer:
If the bar magnet is turned around 180, the neutral point would be on equatorial line and we have
Question 15:
A short bar magnet of magnetic
moment 5.25 × 10–2 JT–1 is placed with its axis
perpendicular to the earth’s field direction. At
what distance from the centre of the magnet the
resultant field is inclined at 45 with earth’s
field on
(i) its normal bisector
(ii) its axis.
Magnitude of the earth’s field at the place is
given to be 0.42 G. Ignore the length of the
magnet in comparison to the distances involved.
Answer:
M = 5.25 × 10–2 JT–1, H = 0.42,
G = 0.42 × 10 –4 T
(i) Since the resultant makes an angle of 45 with
the earth’s field, the magnetic field due to the magnet
must be equal to that of the earth.
For a point on its axis, magnetic field is given by
For a point on its axis, magnetic field is given by