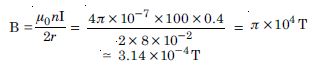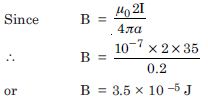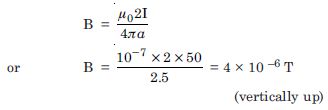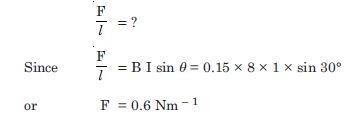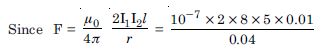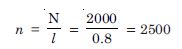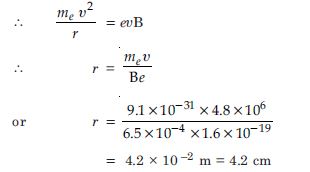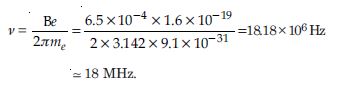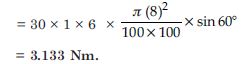The NCERT Solutions for Class 12th Physics are provided at Aasoka for the benefit of students. This helps in better exam preparation so that they can score good marks in their board exams in order to get into their desired career. The students can clear their concepts with the help of NCERT Solutions available for free on Aasoka, the top online learning platform. The study material on Aasoka follows the latest term syllabus hence covering all the topics and concepts accurately.
“Moving Charges and Magnetism” chapter 4 of Physics Class 12 discusses magnetism, its critical concepts, derivations of concepts such as forces between 2 wires carrying current, magnetic force, motion along a magnetic field, and much more. Students will find various questions based on the topics of the syllabus.
Question 1:
A circular coil of wire consisting of
100 turns, each of radius 8.0 cm carries a current
of 0.40 A. What is the magnitude of the magnetic
field
B at the centre of the coil ?
Answer:
Given n = 100, r = 8.0 cm = 8 × 10 –2,
I = 0.4 A, B = ?
At the centre of circular coil
Question 2:
A long straight wire carries a current of 35 A. What is the magnitude of the field
B at
a point 20 cm from the wire ?
Answer:
Given I = 35 A, a = 20 cm = 0.2 m ?
Question 3:
A long straight wire in the horizontal
plane carries current of 50 A in north to south
direction. Give the magnitude and direction of
B at a point 2.5 m east of the wire.
Answer:
Given I = 50 A, B = ?, a = 2.5 m
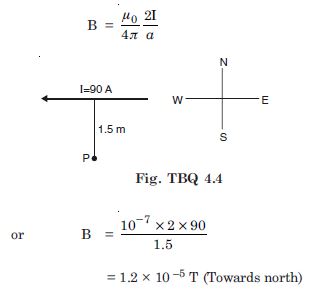
Question 4:
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line ?
Answer:
I = 90 A, a = 1.5 m, B = ?
Question 5:
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8 A and making an angle of 30 with the direction of a uniform magnetic field of 0.15 T ?
Answer:
Given
I = 8A, = 30, B = 0.15 T
Question 6:
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire ?
Answer:
Given l = 3.0 cm = 3 × 10 –2 m, I = 10 A
= 90, B = 0.27 T, F = ?
Since F = BIl sin
F = 0.27 × 10 × (3 × 10 –2) sin 90
= 8.1 × 10 –2 N
Question 7:
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Answer:
GivenI1 = 8.0 A, I 2 = 5.0 A,
r = 4.0 cm = 0.04 m, l = 10 cm = 0.01 m,
= 2 × 10–5 N
(direction is given by Fleming left hand rule)
So we find that the current in the two parallel
wires is flowing in the same direction, so the force
will be normal to A towards B.
Question 8:
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude B inside the solenoid near its centre.
Answer:
Given l = 80 cm = 0.8 m
Total number of turns, N = 5 × 400 = 2000
No. of turns per unit length
D = 1.8 cm, I = 8.0 A
Magnetic field inside the solenoid near its centre
B = μ 0
nI = −
4 × 10-7 × 2500 × 8
= 2.5 × 10 –2 T
Question 9:
A square coil of side 10 cm consists of 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30 with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil ?
Answer:
Given
l = 10 cm = 10 –1 m
So A = 10 –2 m2, n = 20, = 30, B = 0.80 T,
τ = ?, I = 12 A
Since τ = n I AB sin
= 20 × 12 × 10 –2 ×0.8 × sin 30
= 0.96 Nm
Question 10:
Two moving coil meters, M 1 and M 2
have the following particulars :
R1. = 10 , N1 = 30, A1 = 3.6 × 10 –3 m2,
B1 = 0.25 T
R2 = 14 , N2 = 42, A2 = 1.8 × 10 –3 m2,
B2 = 0.50 T
(The spring constants are identical for the
two meters). Determine the ratio of (a) current
sensitivity and (b) voltage sensitivity of M2
and M1.
Answer:
R1. = 10 , N1 = 30, A1 = 3.6 × 10 –3 m2,
B1 = 0.25 T
R2 = 14 , N2 = 42, A2 = 1.8 × 10 –3 m2,
B2 = 0.50 T
Question 11:
In a chamber, a uniform magnetic
field of 6.5 G (1 G = 10 –4 T) is maintained. An
electron is shot into the field with a speed of
4.8 × 106 ms –1 normal to the field. Explain why
the path of the electron is a circle. Determine
the radius of the circular orbit. (e = 1.5 × 10 –19 C,
me = 9.1 × 10 –31 kg).
Answer:
Given B = 6.5, G = 6.5 × 10 –4 J,
= 4.8 × 10 6 ms –1
r = ?, e = 1.6 × 10 –19 C, me= 9.1 × 10 –31 kg
Since B and necessary centripetal force is
provided by magnetic field.
Question 12:
In exercise 4.11, obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron ? Explain.
Answer:
Since frequency of revolution is given by
Question 13:
A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60 with the normal to the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.
Would your answer change if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area ? (All other particulars are also unaltered).
Answer:
n = 30, r = 8 cm
A = (8)2 cm2, I = 6A, B = 1T, = 60
Torque τ = nBIA sin
No, the answer is unchanged because the formula τ = NIA × B is true for a planar loop of any shape.