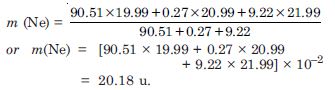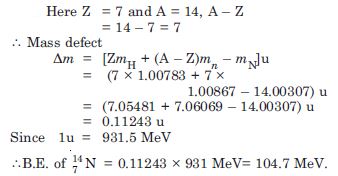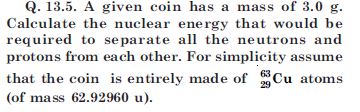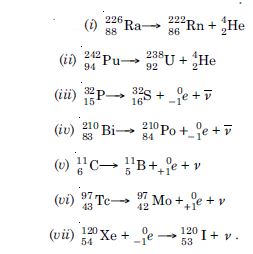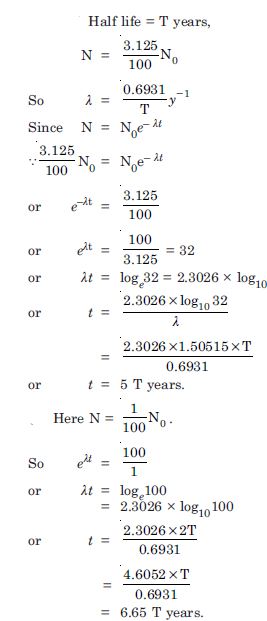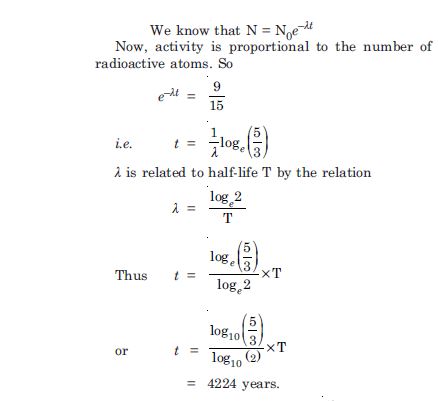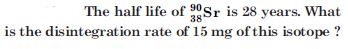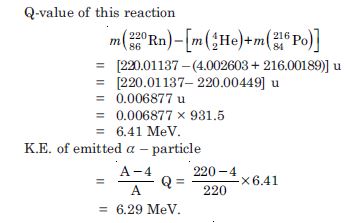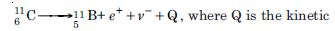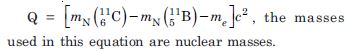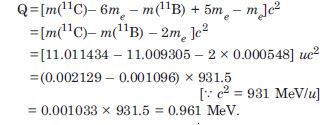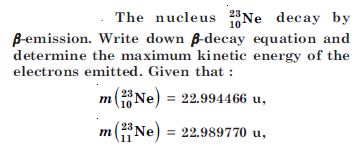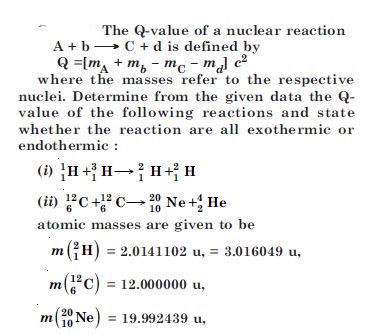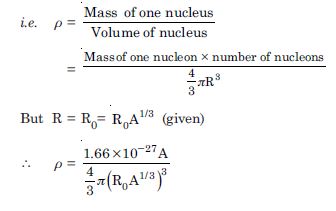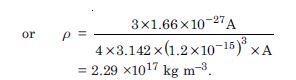Aasoka offers top NCERT Solutions for Class 12 for Physics which will help students prepare for their board exams as well as competitive exams. Even the exam of NEET and JEE is based on the same syllabus. Therefore, NCERT Solutions, which is prepared by subject matter experts, is the best way for students to revise their topics efficiently and effectively. The solutions provide a complete knowledge of the topic of Physics Class 12.
The chapter “Nuclei” of Class 12 Physics consists of topics like radioactivity, atomic masses, size of the nucleus, nuclear binding energy, nuclear energy, the composition of nucleus, mass-energy, nuclear force, mass defect, nuclear fusion, nuclear fission, mass-energy relation, etc. Students can note down important points and formulas to efficiently prepare for the board exams.
Question 1:
Answer:
Question 2:
these isotopes are 19.99 u and 21.99 u respectively. Obtain the average atomic mass of neon.
Answer:
The average atomic mass of neon is
Question 3:
Answer:
Question 4:
Answer:
Question 5:
Answer:
Here Z = 29, A = 63, so A – Z = 34
Mass defect
Question 6:
Answer:
Question 7:
A radioactive isotope has a half-life of T years. After how much time is its activity reduced to (a) 3.125% (b) 1% of its original value ?
Answer:
Question 8:
carbon. Estimate the approximate age of Indus-Valley civilization.
Answer:
Question 9:
Answer:
The rate of decay of radioactive material is given by
Question 10:
Answer:
Question 11:
Answer:
Question 12:
Answer:
Given
energy released in the decay process. The Q of this decay process is given by
Now, if we express the Q value in terms of atomic masses we have to subtract 6m e from the atomic mass of carbon and 5m e from that of boron atomic to get the corresponding nuclear masses. Therefore, we have
Question 13:
Answer:
Question 14:
Answer:
= 0.004958 × 931.5
= + 4.62 MeV ; reaction is exothermic.
Question 15:
Answer:
Question 16:
Answer:
Question 17:
Answer:
Question 18:
Answer:
Question 19:
Calculate the height of the potential barrier for head-on collision of two deuterons, (Hint : The height of the potential barrier if given by the Coulomb repulsion between the two deuterons when they just touch each other.) Assume that they can be taken as hard spheres of radius 2.0 fm.
Answer:
Radius of deuteron r = 2.0 fm
= 2 × 10–15 m
Initial energy of two deuterons = 2KE
This energy is converted into PE, after the headon collision, when deuteron stops and is
given by
Question 20:
From the relation R = R0 A1/3 , where R0 is a constant and A is the mass number of a nucleus. Show that the nuclear matter density is nearly constant (i.e. independent of A).
Answer:
Density of nucleus (). It is defined as the nuclear mass per unit volume.
Thus the nuclear density is of the order of 1017 kgm–3 and is independent of its mass number. Therefore, all nuclei have the same approximate density.
Question 21:
Answer:
Consider the two competing processes :
Case of positron emission