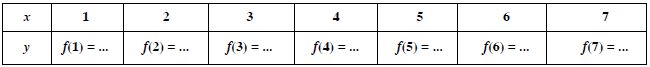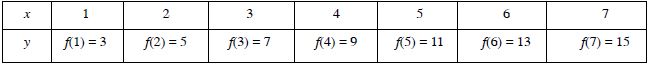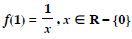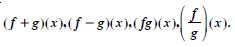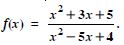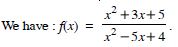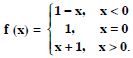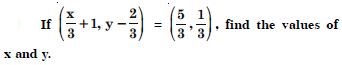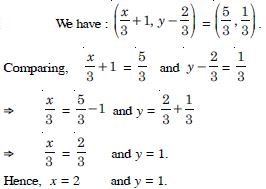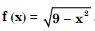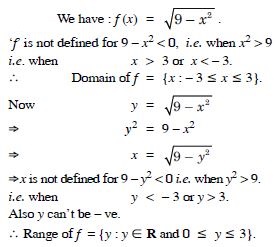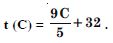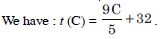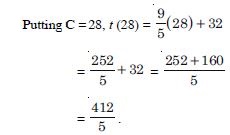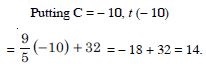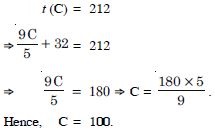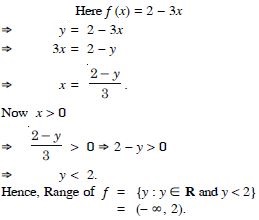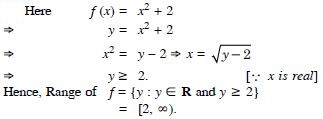Study and get a thorough understanding of the chapter “Relations and Functions” with free NCERT Solutions at Aasoka. These solutions will clear all doubts of students related to the chapter. Students can get well-versed with all the concepts with NCERT Solutions for Class 11 and achieve excellent scores in their exams. The subject matter experts have prepared these solutions which will allow students to efficiently grasp the important concepts. Students must practice Maths regularly to excel in their exams.
Maths Class 11 chapter “Relations and Functions” explains Cartesian product of sets, the definition of relation, function as a special kind of relation from one set to another, domain and range of functions; sum, difference, product, and quotients of functions, pictorial representation of a function, ordered pairs; domain, co-domain and range of a relation, number of elements in the Cartesian product of two finite sets, the real-valued function of the real variable, pictorial diagrams, Cartesian product of the reals with itself; domain, co-domain and range of a function; signum and greatest integer functions with their graphs; polynomial, constant, modulus, identity, rational, and much more.
Question 1:
If (x + 1, y – 2) = (3, 1), find the values of x and y.
Answer:
Since the ordered pairs (x + 1, y – 2) and (3, 1)
are equal,
x + 1 = 3 and y – 2 = 1
x = 2 and y = 3.
Hence, x = 2 and y = 3.
Question 2:
If P = {a, b, c} and Q = {r}, form the sets P × Q and Q × P. Are these products equal
Answer:
We have : P = {a, b, c} and Q = {r}.
P × Q = {(a, r), (b, r), (c, r)}
and Q × P = {(r, a), (r, b), (r, c)}.
Clearly P × Q Q × P. [(a, r)(r,a);etc.]
Question 3:
Let A = {1, 2, 3}, B = {3, 4} and
C = {4, 5, 6}. Find :
A × (B C)
Answer:
Here B C = {3, 4} {4, 5, 6} = {4}.
A × (B C) = {1, 2, 3} × {4}
= {(1, 4), (2, 4), (3, 4)}.
Question 4:
Let A = {1, 2, 3}, B = {3, 4} and
C = {4, 5, 6}. Find :
(A × B) (A × C)
Answer:
Here A × B = {(1, 3), (1, 4), (2, 3), (2, 4),
(3, 3), (3, 4) }
and A × C = {(1, 4), (1, 5), (1, 6), (2, 4),
(2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}.
(A × B) (A × C) = {(1, 4), (2, 4) × (3, 4)}.
Question 5:
Let A = {1, 2, 3}, B = {3, 4} and
C = {4, 5, 6}. Find :
A × (B C)
Answer:
Here B C = {3, 4}{4, 5, 6} = {3, 4, 5, 6}.
A × (B C) = {(1, 3), (1, 4), (1, 5), (1, 6),
(2, 3), (2, 4), (2, 5), (2, 6) (3, 3), (3, 4), (3, 5), (3, 6)}.
Question 6:
Let A = {1, 2, 3}, B = {3, 4} and
C = {4, 5, 6}. Find :
(A × B) (A × C)
Answer:
(A × B) (A × C) = {(1, 3), (1, 4), (1, 5), (1, 6),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}.
Question 7:
If P = {1, 2}, form the set P × P × P.
Answer:
We have : {1, 2}.
P × P × P = {(1, 1, 1), (1, 1, 2), (1, 2, 1),
(2, 1, 1), (1, 2, 2), (2, 1, 2), (2, 2, 1), (2, 2, 2)}.
Question 8:
If R is the set of all real numbers, what do the Cartesian products R × R and R × R × R represent.
Answer:
R × R = {(x, y) : x, y R}, which represents
the co-ordinates of all points in 2-dimensional space.
(ii) R × R × R = {(x, y, z) ; x, y, z R}, which represents
the co-ordinates of all points in 3-dimensional space.
Question 9:
If A × B = {(p, q), (p, r), (m, q), (m, r)}, find A and B.
Answer:
We have A × B = {(p, q), (p, r),(m, q), (m, r)}.
A = set of first elements = {p, m}
and B = set of second elements = {q, r}.
Question 10:
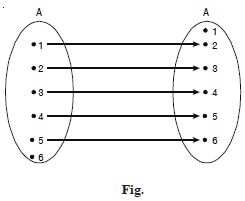
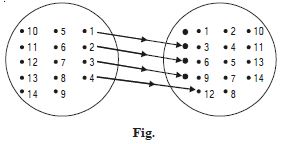
Let A = {1, 2, 3, 4, 5, 6}. Define a
relation R from A to A by
R = {(x, y) : y = x + 1}.
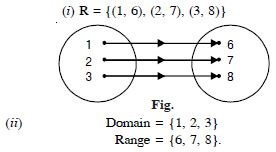
Depict this relation by arrow diagram.
Answer:
By the question, the relation,
R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}.
The arrow diagram is as shown in the figure.
Question 11:
Let A = {1, 2, 3, 4, 5, 6}. Define a
relation R from A to A by
R = {(x, y) : y = x + 1}.
Write down the domain, co-domain and
range of R.
Answer:
Domain = {1, 2, 3, 4, 5}
Range = {2, 3, 4, 5, 6}
and Co-domain = {1, 2, 3, 4, 5, 6}.
Question 12:
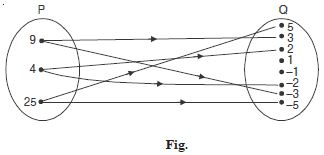
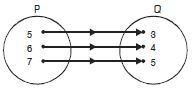
The figure shows a relation between the sets P and Q. Write this relation (i) in set builder form (ii) in roster form What is its domain and range ?
Answer:
Here the relation R is “x is sqaure of y”
(i) In set-builder form :
R = {(x, y) : x is the square of y, x P, y Q}.
In roster form :
R = {(9, 3), (9, – 3), (4, 2), (4, –2), (25, 5), (25, – 5)}.
(ii) Domain of R = {4, 9, 25}.
(iii) Range of R = {– 2, 2, –3 , 3, – 5, 5}.
Question 13:
Set A = {1, 2} and B = {3, 4}. Find the number of relations from A to B.
Answer:
We have : A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}.
Since n(A × B) = 4,
the number of subsets of A × B = 24.
Hence, the number of relations from A to B = 24 = 16.
Question 14:
Let N be the set of natural numbers and
the relation R be defined on N such that :
R = {(x, y) : y = 2x, x, y N}.
What is the domain, co-domain and range of R ?
Is this relation a function ?
Answer:
Domain of R = N, the set of natural numbers.
Co-domain of R = N, the set of natural numbers.
Range of R = set of even natural numbers.
Since each natural number n has one and only one image,
the relation R is a function.
Question 15:
Examine each of the following relations
given below and state in each case, giving reasons whether
it is a function or not ?
R = {(2, 1), (3, 1), (4, 2)}
Answer:
Since the elements 2, 3, 4 in the domain of
R have unique images,
R is a function.
Question 16:
Examine each of the following relations
given below and state in each case, giving reasons whether
it is a function or not ?
R = {(2, 2), (2, 4), (3, 3), (4, 4)}
Answer:
Since the element 2 in the domain of R has two images
2 and 4,
R is not a function.
Question 17:
Examine each of the following relations
given below and state in each case, giving reasons whether
it is a function or not ?
R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}
Answer:
Since each element in the domain of R has a unique
image,
R is a function.
Question 18:
Let N be the set of natural numbers. Define a real valued function f : N N by 2x + 1. Using this definition, complete the table given below :
Answer:
The completed table is given by :
[ f(1) = 2 (1) + 1 = 3, f(2) = 2(2) + 1 = 5; etc.]
Question 19:
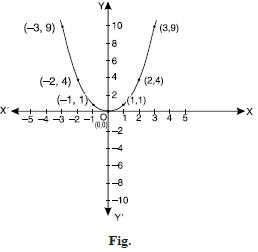
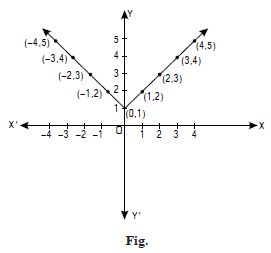
Define the function f : RR by f (x) = x2, x R. Complete the table given below by using this definition.
What is the domain and range of this function ?
Draw the graph of f.
Answer:
The complete table is as below :
Domain of f = {x : x R}.
Range of f = {x : x ≥ 0, x R}.
The graph of f is as in the adjoining figure.
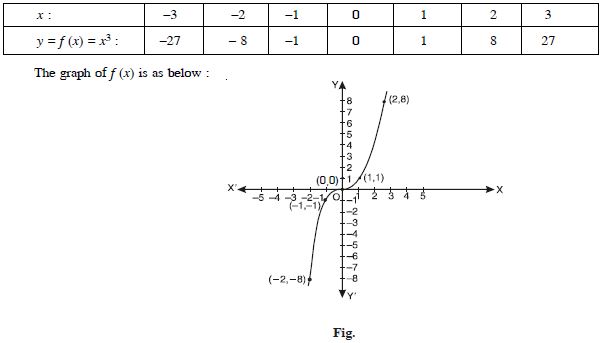
Question 20:
Draw the graph of the function :
f : R R defined by f (x) = x3, x R.
Answer:
We have the following table :
Question 21:
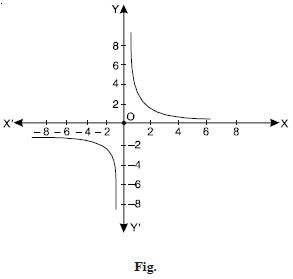
Define the real valued function f : R – {0} R defined by :
Complete the table given below using this defnition.
What is the domain and range of this function ?
Answer:
The complete table is as below.
Domain of f = R – {0}.
Range of f = R – {0}.
The graph of f is as shown in the following figure :
Question 22:
Let f(x) = x2 and g(x) = 2x + 1 be two real functions. Find :
Answer:
Question 23:
Answer:
Question 24:
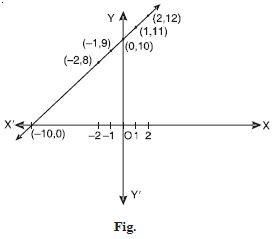
Let R be the set of real numbers. Define a real function f : R R by f (x) = x + 10. Sketch the graph of this function.
Answer:
We have the following table :
The graph of the function is as shown below :
Question 25:
Let R be a relation from Q to Q defined by :
R = {(a, b) : a, b Q and a – b Z}.
Show that : (a, a) R for all Q Q
Answer:
Since a – a = 0 Z, therefore, (a, a) R.
Question 26:
Let R be a relation from Q to Q defined by :
R = {(a, b) : a, b Q and a – b Z}.
Show that : (a, b) R implies that (b, a) R
Answer:
(a, b) R a – b Z b – a Z (b, a) R.
Question 27:
Let R be a relation from Q to Q defined by :
R = {(a, b) : a, b Q and a – b Z}.
Show that : (a, b) R and (b, c) R implies that (a, c) R
Answer:
(a, b) R and (b, c) R
a – b Z and b – c Z
(a – b) + (b – c) = a – c Z.
Hence, (a, c) R.
Question 28:
Let f = {(1, 1), (2, 3), (0, – 1), (– 1, – 3)} be a linear function from Z to Z. Find f(x).
Answer:
Since ‘f’ is linear function,
let f(x) = mx + c ...(1)
Now (1, 1) R 1 = m + c m + c = 1 ...(2)
And (0, – 1) R – 1 = 0 + c c = – 1.
Putting in (2), m – 1 m = 2.
Putting in (1), f(x) = 2x – 1.
Question 29:
Find the domain of the function :
Answer:
Now x2 – 5x + 4 = (x – 4) (x – 1).
x2 – 5x + 4 = 0 x = 4, 1.
Thus, that function ‘f’ is defined for all real value except
at x = 4, 1.
Hence, domain of f = R – {1, 4}.
Question 30:
The function ‘f’ is defined by :
Draw the graph of f (x).
Answer:
We have : f (x) = 1– x, x < 0.
f (– 4) = 1 – (– 4) = 1 + 4 = 5
f (–3) = 1 – (–3) = 1 + 3 = 4
f (–2) = 1 – (–2) = 1 + 2 = 3
f (–1) = 1 – (–1) = 1 + 1 = 2.
Also, f (0) = 1.
And f (x) = x + 1, x > 0.
f (1) = 1 + 1 = 2, f (2) = 2 + 1 = 3,
f (3) = 3 + 1 = 4, f (4) = 4 + 1 = 5 ; .....
Hence, the graph of f is as shown :
Question 31:
Answer:
Question 32:
If the set A has 3 elements and the set B =
{3, 4, 5}, then find the number of elements in
(A × B).
Answer:
A has 3 elements and B has also 3 elements.
Number of elements in (A × B) = 3 × 3 = 9.
Question 33:
If G = {7, 8}, H = {5, 4, 2}, find G × H and H × G.
Answer:
(i) G × H = {7, 8} × {5, 4, 2}
= {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}.
(ii) H × G = {5, 4, 2} × {7, 8}
= {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}.
Question 34:
State whether each of the following statements are
true or false. If the statement is false, rewrite the given
statement correctly.
If P = {m, n}
Q = {n, m},
then P × Q = {(m, n), (n, m)}.
Answer:
False.
P × Q = {(m, n), (m, m), (n, m) (n, n)}.
Question 35:
State whether each of the following statements are
true or false. If the statement is false, rewrite the given
statement correctly.
If A and B are non-empty sets, then A × B is nonempty
set of ordered pairs (x, y) such that x Β and
y A.
Answer:
False.
A × B is a non-empty set of ordered pairs.
(x, y) such that x A and y B.
Question 36:
State whether each of the following statements are
true or false. If the statement is false, rewrite the given
statement correctly.
If A = {1, 2}, B = {3, 4}, then :
A × (B ) = .
Answer:
True.
[ B = , A × (B ) = A × = ]
Question 37:
If A = {– 1, 1}, find A × A × A.
Answer:
A × A × A ={– 1, 1} × {– 1, 1} × {– 1, 1}
= {(– 1, – 1, – 1), (– 1, – 1, 1),
(– 1, 1, – 1), (– 1, 1, 1), (1, – 1, – 1),
(1, – 1, 1), (1, 1, – 1), (1, 1, 1)}.
Question 38:
If A × B = [(a, x), (a, y), (b, x), (b, y)}, find A and B.
Answer:
We have :
A = {(a, x), (a, y), (b, x), (b, y)}.
A = {a, b} and B = {x, y}.
Question 39:
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and
D = {5, 6, 7, 8].
Verify that :
A × (B C) = (A × B) (A × C)
Answer:
B C = {1, 2, 3, 4} {5, 6} = .
LHS = A × (B C) = A ×
= {1, 2} × = .
Now A × B = {1, 2} × {1, 2, 3, 4}
= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
and A × C = {1, 2} × {5, 6}
= {(1, 5), (1, 6), (2, 5), (2, 6)}.
RHS = (A × B) (A × C) = .
Hence, A × (B C) = (A × B) (A × C).
Question 40:
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and
D = {5, 6, 7, 8].
Verify that :
A × C is a subset of B × D.
Answer:
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
[As in part (i)]
B × D = {1, 2, 3, 4} × {5, 6, 7, 8}
= {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6),
(2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8),
(4, 5), (4, 6), (4, 7), (4, 8)}.
Clearly each element of A × C is in B × D.
Hence, A × C is a subset of B × D.
Question 41:
Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have ? List them.
Answer:
A × B = {1, 2} × {3, 4}
= {(1, 3), (1, 4), (2, 3), (2, 4)}.
No. of subsets of A × B = 24 = 16.
These subsets are :
, {(1, 3)}, {(1, 4)}, {(2, 3)},
{(2, 4)},{(1, 3), (1,4)}, {(1, 3), (2, 3)}, {(1, 3), (2, 4},
{(1, 4), (2, 3)}, {((1, 4), (2, 4)}, {(2, 3), (2, 4)},
{(1, 3), (1, 4), (2, 3)}, {(1, 4), (2, 3), (2, 4)},
{((2, 3), (2, 4), (1, 3))}, {(1, 3), (1, 4), (2, 4)},
{(1, 3), (1, 4), (2, 3), (2, 4)}.
Question 42:
Let A and B be two sets such that n (A) = 3, n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
Answer:
Since x, y, z A,
A = {x, y, z}.
Since 1, 2 B,
B = {1, 2}.
Question 43:
The cartesian product A × A has 9 elements among which are found (– 1, 0) and (0, 1). Find the set A and the remaining elements of A × A.
Answer:
Here (– 1, 0) A × A
and (0, 1) A × A.
– 1, 0 A
and 0, 1 A.
Thus A = {– 1, 0, 1}.
A × A = {– 1, 0, 1} × {– 1, 0, 1}
= {(– 1, – 1), (– 1, 0), (– 1, 1), (0, – 1),
(0, 0), (0, 1), (1, – 1), (1, 0), (1, 1)}.
Remaining elements of A × A are :
(– 1, – 1), (– 1, 1), (0, – 1), (0, 0), (1, – 1), (1, 0), (1, 1).
Question 44:
Let A = {1, 2, 3, ........., 14}. Define a relation R from A to A by R = {(x, y) ; 3x – y = 0, where x, y A}. Write down its domain, co-domain and range.
Answer:
Here R = {(x, y) : 3x – y = 0, where x, y A}
= {(1, 3), (2, 6), (3, 9), (4, 12)}.
(i) Domain = {1, 2, 3, 4}
(ii) Co-domain = {1, 2, 3, ......., 14}
(iii) Range = {3, 6, 9, 12}.
Question 45:
Define a relation R on the set N of natural numbers
by R = {(x, y) : y = x + 5, x is a natural number less
than 4 ; x, y N}.
Depict this relationship using (i) roster form (ii) an
arrow diagram. Write down the domain and range.
Answer:
Question 46:
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R
from A to B by :
R= {(x, y) : the difference between x and y is odd ;
x A, y B}. Write R in roster form.
Answer:
Here R = {(1, 4), (1, 6), (2, 9), (3, 4),
(3, 6), (5, 4), (5, 6)}
[ 4 – 1 = 3; odd etc.]
Question 47:
Figure given below shows a relationship between the sets P and Q. Write the relation (i) in set builder form (ii) roster form. What is its domain and range ?
Answer:
(i) R = {(x, y) : x – y = 2, 4 < x < 8, x, y N}
(ii) R = {(5, 3), (6, 4), (7, 5)}.
Domain = {5, 6, 7}. Range = { 3, 4, 5}.
Question 48:
Write the relation ?
R = {(x, x3) : x is a prime number less than 10}
in roster form.
Answer:
Prime numbers less than 10 are 2, 3, 5, 7.
R = {(2, 8), (3, 27), (5, 123), (7, 343)}.
Question 49:
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A into B.
Answer:
We have : A = {x, y, z}
and B = {1, 2}.
A × B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}.
n (A × B) = 6
the number of subsets of n (A × B) = 26.
Hence, the number of relation from A into B = 26.
Question 50:
Let R be the relation on Z defined by :
R = {(a, b) : a, b Z, a – b is an integer}
Find the domain and range of R.
Answer:
We have : R = {(a, b) : a, b Z,
a – b is an integer}
Domain of R = Z.
Range of R = Z.
Question 51:
Which of the following relations are functions ? Give
reasons. If it is a function, determine its domain and
range :
{(2, 1), (5, 1), (8, 1) (11,1), (14, 1), (17, 1)}
Answer:
We have :
f = {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}.
Here no two ordered pairs have the same first component.
this relation is a function.
Domain of f = {2, 5, 8, 11, 14, 17}.
Range of f = {1}.
Question 52:
Which of the following relations are functions ? Give
reasons. If it is a function, determine its domain and
range :
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Answer:
We have : f = {(2, 1), (4, 2), (6, 3), (8, 4),
(10, 5), (12, 6), (14, 7)}.
Here no two ordered pairs have the same first component.
this relation is a function.
Domain of f = {2, 4, 6, 8, 10, 12, 14}.
Range of f = {1, 2, 3, 4, 5, 6, 7}.
Question 53:
Which of the following relations are functions ? Give
reasons. If it is a function, determine its domain and
range :
{(1, 3), (1, 5), (2, 5)}
Answer:
We have : f = {(1, 3), (1, 5), (2,5)}.
Here 1 appears more than once as a first component in the
ordered pairs of f.
Hence, this relation is not a function.
Question 54:
Find the domain and range of the following real functions :
f (x) = – | x |
Answer:
We have : f (x) = – | x |.
Clearly f (x) 0 ∀ x R.
Domain of f = R.
Range of f = (– , 0].
Question 55:
Find the domain and range of the following real functions :
Answer:
Question 56:
A function f is defined by f (x) = 2x – 5. Write down
the values of :
f (0)
Answer:
We have : f (x) = 2x – 5.
f (0) = 2 (0) – 5 = 0 – 5 = – 5.
Question 57:
A function f is defined by f (x) = 2x – 5. Write down
the values of :
f (7)
Answer:
We have : f (x) = 2x – 5.
f (7) = 2 (7) – 5 = 14 – 5 = 9.
Question 58:
A function f is defined by f (x) = 2x – 5. Write down
the values of :
f (– 3)
Answer:
We have : f (x) = 2x – 5.
f (– 3) = 2 (– 3) – 5 = – 6 – 5 = – 11.
Question 59:
The function ‘f’, which maps temperature in degree celsius into temperature degree Fahrenheit is defined by
Find :
t (0)
Answer:
Putting C = 0, t (0) = 0 + 32 = 32.
Question 60:
The function ‘f’, which maps temperature in degree celsius into temperature degree Fahrenheit is defined by
Find :
t (28)
Answer:
Question 61:
The function ‘f’, which maps temperature in degree celsius into temperature degree Fahrenheit is defined by
Find :
t (– 10)
Answer:
Question 62:
The function ‘f’, which maps temperature in degree celsius into temperature degree Fahrenheit is defined by
Find :
The value of C, when t (C) = 212
Answer:
Question 63:
Find the range of each of the following function :
f (x) = 2 – 3x, x R, x > 0
Answer:
Question 64:
Find the range of each of the following function :
f (x) = x2 + 2, x is a real number
Answer:
Question 65:
Find the range of each of the following function :
f (x) = x, x is a real number
Answer:
We have f (x) = x y = x.
But x is a real number
y is a real number.
Hence, Range of f = {y : y R}
= R.